空间滤波(基于opencv)

最新推荐文章于 2025-05-27 15:39:19 发布

原创最新推荐文章于 2025-05-27 15:39:19 发布 · 1.1k 阅读

CC 4.0 BY-SA版权

文章标签：

空间滤波是图像处理中的一种技术，通过在图像的每个像素周围应用滤波器，改变其值来实现图像的平滑、锐化或边缘检测等效果。图像的线性空间滤波是指图像与滤波器核进行卷积操作。常见的空间滤波器包括均值滤波器、高斯滤波器、Sobel滤波器等，用于去噪、增强图像细节或突出边缘特征。空间滤波广泛应用于图像去噪、特征提取和质量改善等领域。

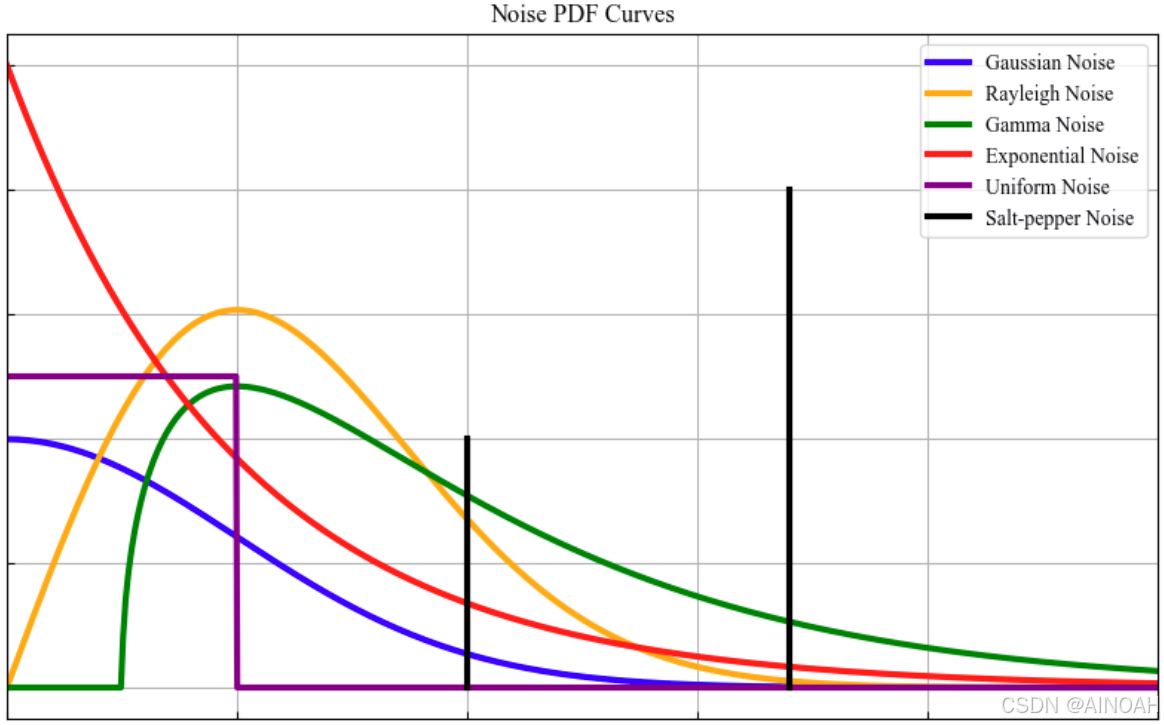
一.常见噪声的概率密度函数

1.高斯噪声

$p(z)=\frac{1}{\sqrt{2\pi }\sigma }e^{-(z-\bar{z})/2\sigma ^{2}}$

均值是 $\bar{z}$ ，方差是 $\sigma$

z值在区间 $\bar{z}\pm \sigma$ 内的概率是0.68，z值在区间 $\bar{z}\pm 2\sigma$ 内的概率是0.95。

2.Rayleigh噪声

$p(z)=\left\{\begin{matrix} \frac{2}{b}(z-a)e^{-(z-a)^{2}/b} ,z\geqslant a\\0 ,z< a\end{matrix}\right.$

均值是 $\bar{z}=a+\sqrt{\pi b/4}$ ，方差为 $\sigma ^{2}=\frac{b(4-\pi )}{4}$

Rayleigh噪声的曲线特点是基本形状右偏。Rayleigh噪声的概率密度形式对整体趋势倾斜的颜色直方图建模非常有效。

3.Gamma噪声

$p(z)=\left\{\begin{matrix} \frac{a^{b}z^{b-1}}{(b-1)!}e^{-az} ,z\geqslant 0\\0 ,z< a\end{matrix}\right.$

均值是 $\bar{z}=\frac{b}{a}$ ，方差是 $\sigma ^{2}=\frac{b}{a^{2}}$

4.指数噪声

$p(z)=\left\{\begin{matrix} ae^{-az} ,z\geqslant 0\\ 0 ,z< 0 \end{matrix}\right.$

均值是 $\bar{z}=\frac{1}{a}$ ，方差是 $\sigma _{2}=\frac{1}{a^{2}}$

5.均匀噪声

$p(z)=\left\{\begin{matrix} \frac{1}{b-a} , a\leqslant z\leqslant b\\ 0 ,else \end{matrix}\right.$

均值是 $\bar{z}=\frac{a+b}{2}$ ，方差是 $\sigma ^{2}=\frac{(b-a)^{2}}{2}$

6.椒盐噪声

$p(z)=\left\{\begin{matrix} P_{s} ,z=2^{k}-1\\ P_{p} ,z=0 \\ 1-(P_{s}+P_{p}) ,z=V\end{matrix}\right.$

其中，V是区间 $0< V< 2^{k}-1$ 内的任意数值。若 $P_{s}$ 和 $P_{p}$ 都不为0，尤其是当他们相等的时候，满足椒盐噪声的概率密度的噪声值将是白色的或者黑色的，在图像上就表现为盐粒和胡椒那样的随机分布，所以称为椒盐噪声。

# Gaussian noise
gaussian_noise = np.random.normal(0, 1.4, img_org.shape).astype(np.float32)
noisy_img = img_org + gaussian_noise * 10
# Rayleigh noise
scale_parameter = 1.6
rayleigh_noise = np.random.rayleigh(scale_parameter, img_org.shape).astype(np.float32)
rayleigh_img = img_org + rayleigh_noise * 10
# Gamma noise
gamma_noise = np.random.gamma(1.5, 1, img_org.shape)
gamma_img = img_org + gamma_noise * 10
# Exponential noise
exponential_noise = np.random.exponential(1, img_org.shape)
e_img = img_org + exponential_noise * 10
# Uniform noise
uniform_noise = np.random.uniform(-20, 20, img_org.shape)
u_img = uniform_noise + img_org
# Salt-pepper noise
sp_img = np.copy(img_org)
salt_prob = 0.05
pepper_prob = 0.05
salt_mask = np.random.rand(*img_org.shape) < salt_prob
sp_img[salt_mask] = 255
pepper_mask = np.random.rand(*img_org.shape) < pepper_prob
sp_img[pepper_mask] = 0

不同噪声的分布可视化：

示例图像的原图和灰度直方图：

下图添加了不同的噪声的图像和对应图像的直方图，可以从灰度直方图中直观的看出不同分布的噪声对原始图像灰度的影响。

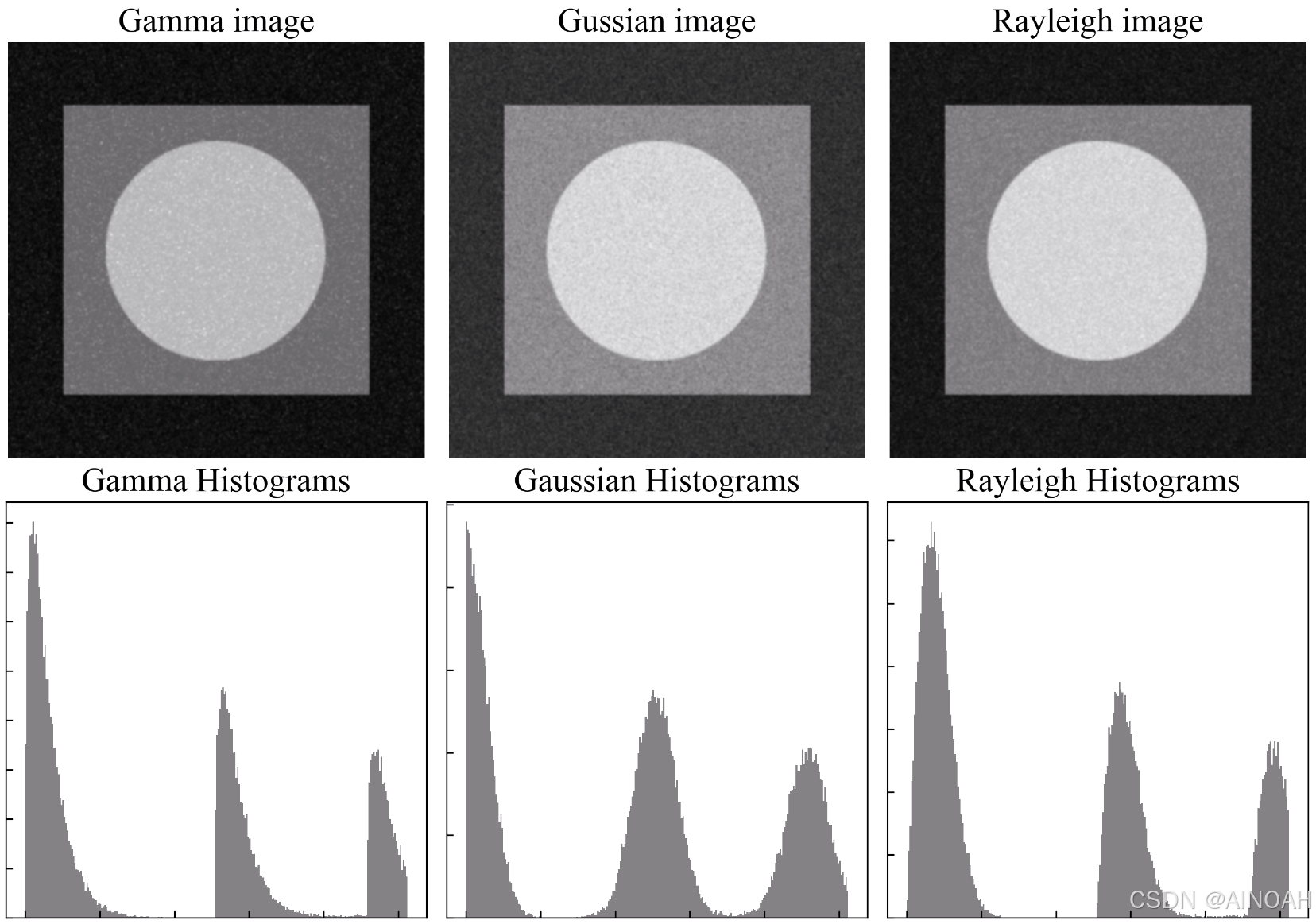
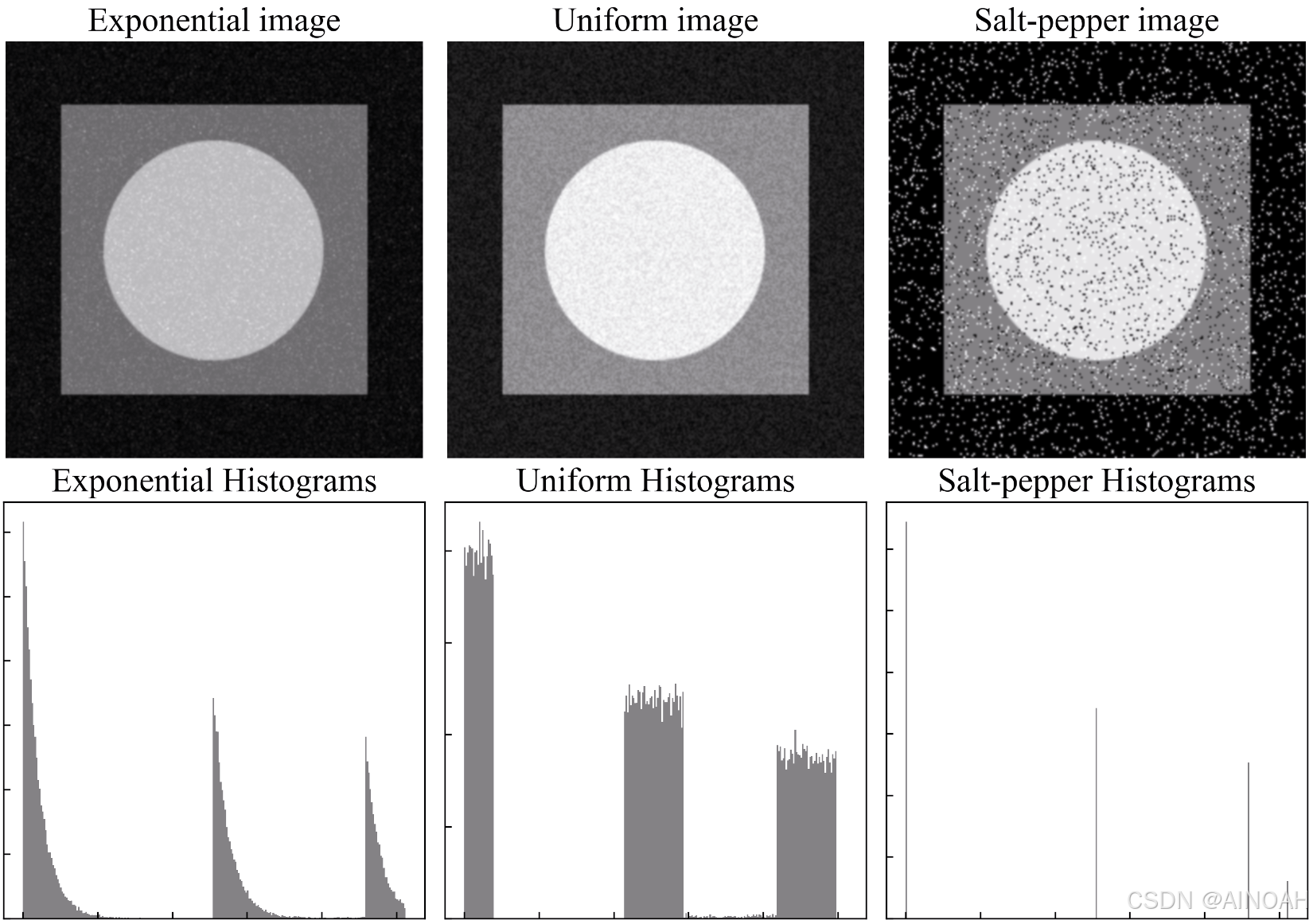
二.均值滤波

当一幅图像仅被加性噪声干扰退化时，可以表示为：

$g(x,y)=f(x,y)+\eta (x,y)$

当仅存在加性噪声时，可以用空间滤波的方法来估计f(x,y)，即图像去噪。

1.算术平均滤波

令 $S_{xy}$ 表示中心为(x,y)、大小为 $m\times n$ 的矩形子图窗口的一组坐标。算术平均滤波器在由 $S_{xy}$ 定义的区域中，计算噪声图像g(x,y)的平均值，去噪后的图像为：

$\hat{f}(x,y)=\frac{1}{mn}\sum_{(u,v)\in S_{xy}} g(u,v)$

其中，u和v是领域 $S_{xy}$ 中包含的像素坐标。简单来说，算术平均滤波可以通过计算图像局部区域像素值的平均值来实现平滑效果，在python中可以利用归一化卷积框完成滤波。

cv2.blur(src, ksize[, dst[, anchor[, borderType]]])
"""
src：输入图像，可以是单通道（灰度图）或多通道（彩色图）
ksize：卷积核大小,通常传入一个元组，只能是奇数尺寸
dst（可选）：输出图像，类型与输入图像相同。
anchor（可选）：指定卷积核的锚点（中心点）。默认为 (-1, -1)，表示自动选择卷积核的中心点。
borderType（可选）：边界像素填充方式，默认值是 cv2.BORDER_DEFAULT。可选值包括：
cv2.BORDER_CONSTANT：用常量值填充。
cv2.BORDER_REPLICATE：复制边缘像素值。
cv2.BORDER_REFLECT：以边界为对称轴进行反射。
cv2.BORDER_WRAP：将边界像素看作周期性重复。
"""

选择5x5的核进行算术平均

kernel_size = (5, 5)
fil_g_img = cv2.blur(g_image, kernel_size)
fil_r_img = cv2.blur(r_image, kernel_size)
fil_gamma_img = cv2.blur(gamma_image, kernel_size)

可以看到，利用5x5的归一化核进行平均后得到去噪的图片，其灰度直方图的趋势和原图类似（在特定灰度处呈细高状态）。算术平均滤波是通过取邻域像素的平均值来处理每个像素，可以明显的去除噪声，但是会导致图像中的细节被模糊。

算术平均滤波的局限性：

图像细节被模糊边缘被模糊
不能区分无用噪声和有用信号
不能适应局部变化

2.几何均值滤波

几何均值滤波是利用局部像素值的几何均值来替代中心像素的值。与算术平均滤波不同，几何均值滤波计算的是邻域像素值的乘积的n次方根（n为邻域像素的数量），而不是它们的算术平均。这种滤波方法对噪声，特别是乘性有较强的鲁棒性。使用几何均值滤波的图像为：

$\hat{f}(x,y)=[\prod_{(u,v)\in S_{xy}}g(u,v)]^{\frac{1}{mn}}$

其中，mn是 $S_{xy}$ 区域的所有像素之积。

from scipy.ndimage import generic_filter
def geometric_mean_filter(input):
    product = np.prod(input)
    n = input.size
    return product**(1/n)

g_image = cv2.imread(r'D:\pythonwork\imagepro\data\g_image.tif', cv2.IMREAD_GRAYSCALE)
r_image = cv2.imread(r'D:\pythonwork\imagepro\data\r_image.tif', cv2.IMREAD_GRAYSCALE)
gamma_image = cv2.imread(r'D:\pythonwork\imagepro\data\gamm_image.tif', cv2.IMREAD_GRAYSCALE)

kernel_size = 3
filtered_g = generic_filter(g_image, geometric_mean_filter, size=kernel_size)
filtered_r = generic_filter(r_image, geometric_mean_filter, size=kernel_size)
filtered_gamma = generic_filter(gamma_image, geometric_mean_filter, size=kernel_size)
filtered_e = generic_filter(e_image, geometric_mean_filter, size=kernel_size)
filtered_u = generic_filter(u_image, geometric_mean_filter, size=kernel_size)
filtered_sp = generic_filter(sp_image, geometric_mean_filter, size=kernel_size)

几何均值滤波的劣势：

计算复杂度相对较高，需要计算领域内的像素值乘积和mn次方根
不适用于加性噪声
对灰度为0的像素值非常敏感

3.谐波平均滤波

谐波平均滤波器是一种非线性图像滤波器，通常用于去除图像中的椒盐噪声，使用谐波平均滤波的图像为：

$\hat{f}(x,y)=\frac{mn}{\sum_{(u,v)\in S_{xy}}\frac{1}{g(u,v)}}$

谐波平均滤波器对图像中的高值（亮点）较为敏感，因此能够有效去除椒盐噪声中的“盐”（亮点）部分。与线性滤波器（如均值滤波器）不同，谐波平均滤波器属于非线性滤波，它通过考虑像素值的倒数进行加权平均，因此对极端值有较强的抑制作用。

def harmonic_mean_filter(img, kernel_size):
    rows, cols = img.shape
    pad = kernel_size  // 2
    padded_img = np.pad(img, pad, mode='constant', constant_values=0)
    output_img = np.zeros_like(img)
    # 对每个像素进行滤波
    for i in range(rows):
        for j in range(cols):
            # 获取邻域区域
            neighbor = padded_img[i:i+pad+2, j:j+pad+2]
            # 计算谐波平均值
            harmonic_mean = np.sum(1.0 / (neighbor + 1e-5))
            output_img[i, j] = (kernel_size**2) * np.reciprocal(harmonic_mean)
    
    return output_img