数字图像灰度变换(基于opencv)

原创于 2024-09-25 17:12:12 发布 · 1.2k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#opencv #计算机视觉 #python

opencv图像处理专栏收录该内容

3 篇文章

订阅专栏

空间域指的是图像平面本身，空间域中的图像处理方法直接对图像中的像素进行处理。灰度变换是一种常见的数字图像处理技术，旨在空间域中调整图像像素的灰度值，以改善图像质量或实现特定的视觉效果。

在空间域处理基于：

$g(x,y)=T[f(x,y)]$

其中，f(x,y)是输入图像，g(x,y)是输出图像，T是在点(x,y)领域上定义的针对f的变换矩阵(算子)。

1. 图像反转

图像反转变换是常见的线性变换，图像反转变换函数： $s=L-1-r$

归一化后的反转变换函数图像：

通过这个函数得到的灰度级在[0,L-1]，类似于胶片的感觉。

L = 256
conv_img = L - 1 - image_grey

2. 对数变换

不满足加性和同质性的变换是非线性变换，对数变换是常用的数字图像非线性变换，对数变换的通式是： $s=clog(1+r)$ ，其中c是常数，并假设 $r\geq 0$ 。

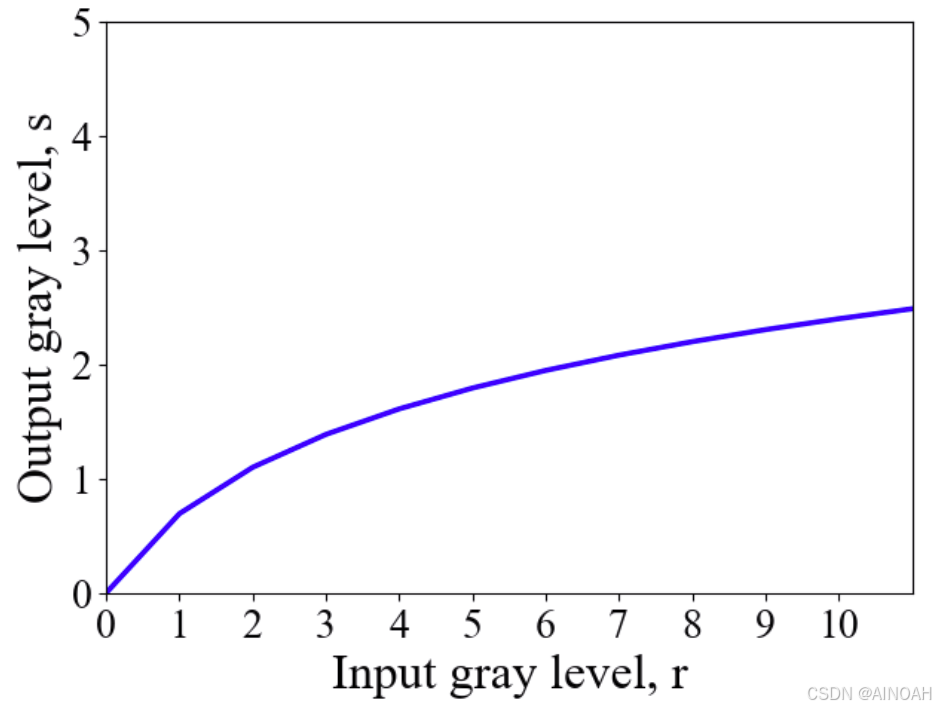
c = 0.17
f_img = image_grey.astype(np.float32)
log_img = c * np.log(1 + f_img)

对数变换是对原图的逐像素实现对数变换的映射，由对数函数的趋势可知，斜率单调递减，因此对于数字图像处理来说，可以扩展低亮度区域，压缩高亮度区域，从而提高图像的可视化效果。

3. 伽马变换

伽马变换的形式是： $s=cr^{^{\gamma }}$ ，其中 $c$ 和 $\gamma$ 都是正常数。

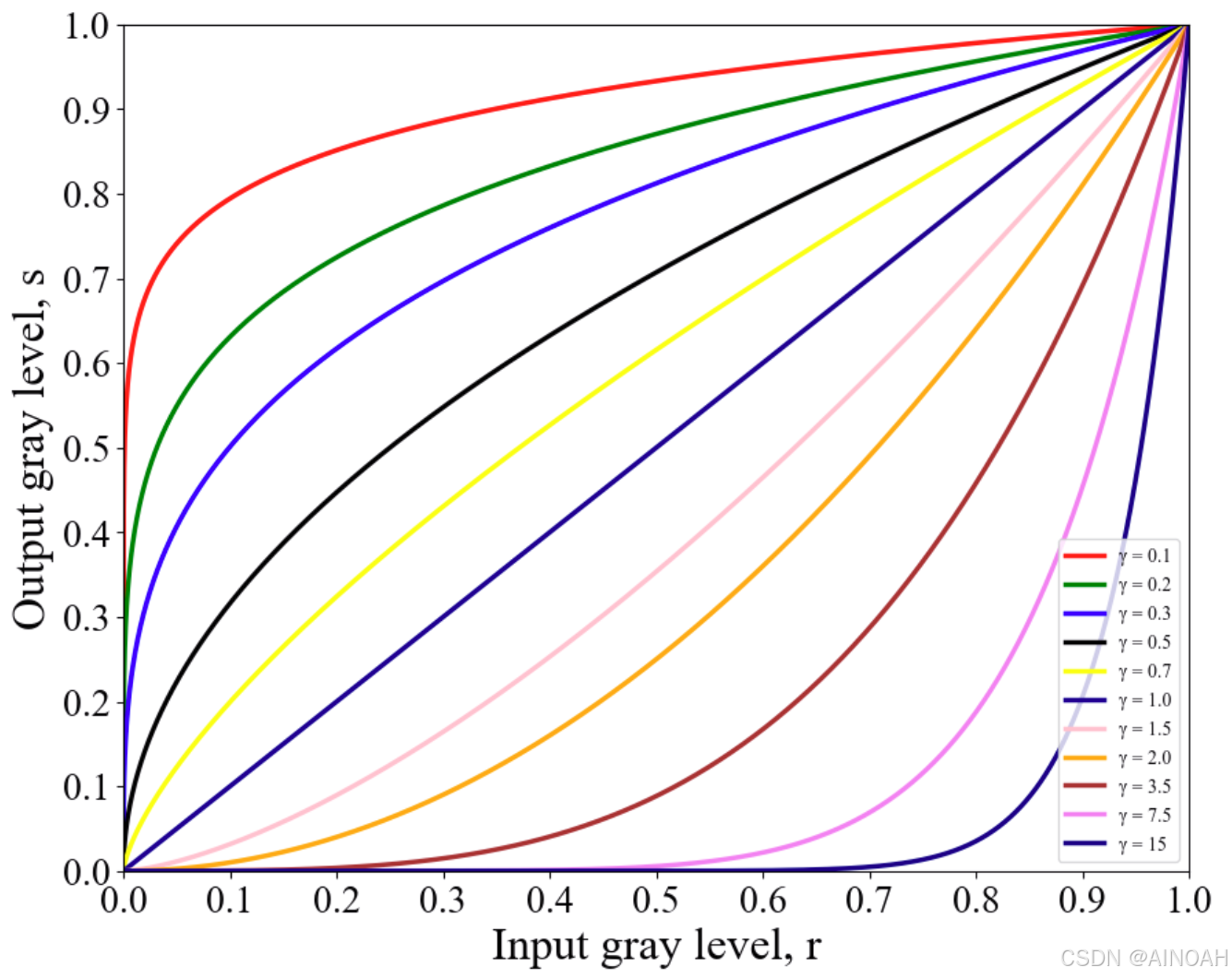
考虑到偏移时，也可以写为： $s=c(r+\varepsilon )^{\gamma }$

伽马变换可以改变图像的对比度：

$\gamma > 1$ ：使暗区更暗，亮区更亮； $\gamma < 1$ ：使暗区更亮，亮区压缩； $c=\gamma =1$ ：恒等变换。

def gamma_transformation(image, gamma):
    # 归一化图像
    normalized_img = image / 255.0
    # 伽马变换
    gamma_corrected = np.power(normalized_img, gamma)
    # 还原到 [0, 255] 并转换为 uint8 类型
    result = np.uint8(gamma_corrected * 255)
    return result

如果是三通道彩色数字图像，需要对每个通道都进行变换

def gamma_transformation_color(image, gamma):
    normalized_img = image / 255.0
    gamma_corrected = np.power(normalized_img, gamma)
    result = np.uint8(gamma_corrected * 255)
    return result

gamma_values = [0.4, 0.7, 1.0, 1.5, 2.0]
image_brg = cv2.cvtColor(image_brg, cv2.COLOR_BGR2RGB)

plt.figure(figsize=(10, 7),dpi=300)
plt.subplot(2, 3, 1)
plt.title('Original Image', fontsize=16)
plt.imshow(image_brg)
plt.axis('off')

for i, gamma in enumerate(gamma_values):
    transformed_img = gamma_transformation_color(image_brg, gamma)
    plt.subplot(2, 3, i + 2)
    plt.title(f'Gamma = {gamma}', fontsize=16)
    plt.imshow(transformed_img)
    plt.axis('off')
plt.tight_layout()
plt.show()

4. 分段线性变换

分段线性变换通过将输入灰度值映射到不同的区间，使图像的亮度和对比度得到调整。其原理是将整个灰度范围划分为若干段，并对每一段应用不同的线性变换，使得灰度值在不同区间内按照相应的线性关系进行映射。分段线性变换函数的优点是其形式可以任意复杂。

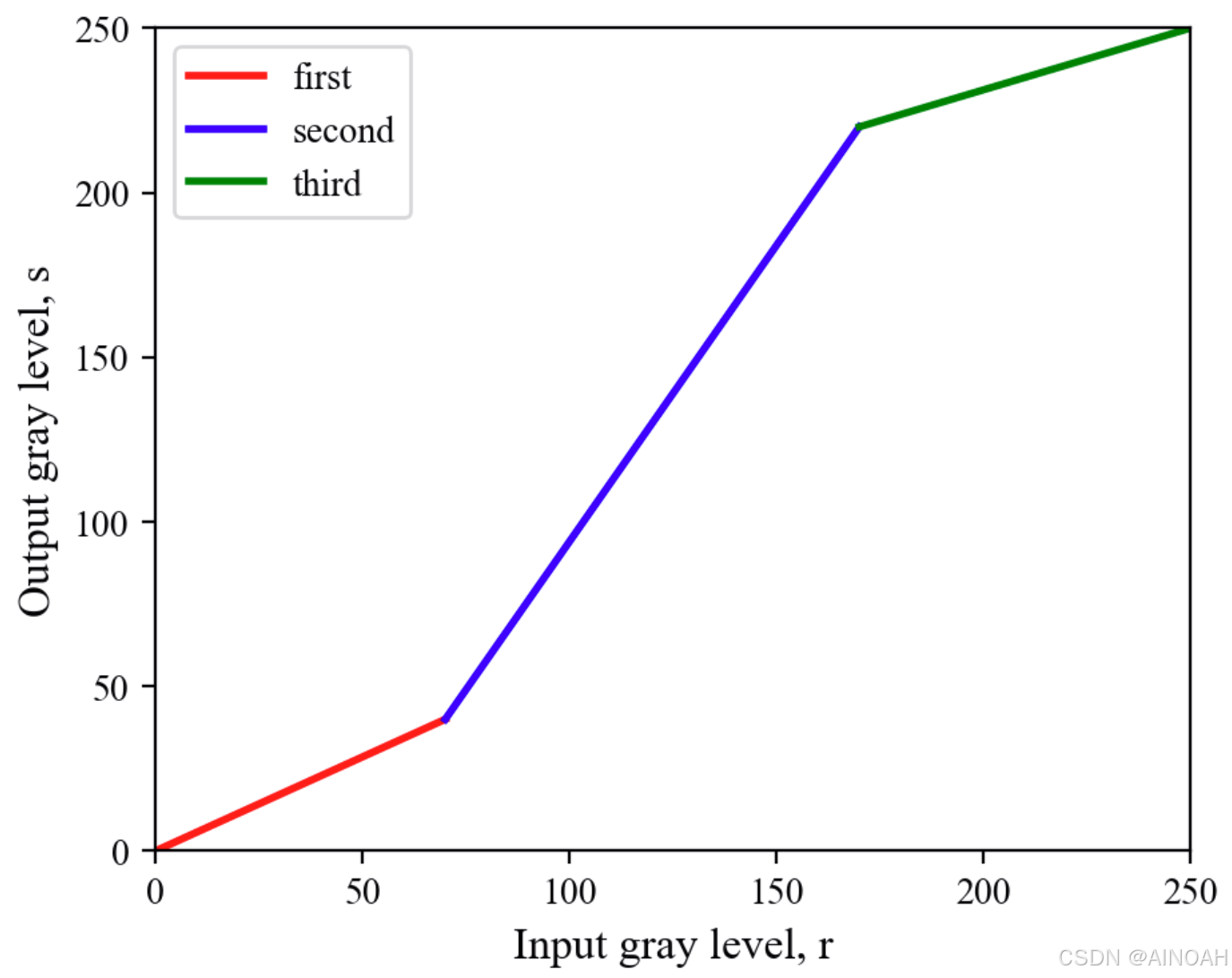
光照不足、成像传感器的动态范围偏小、图像获取过程中镜头参数的设置不当都有可能导致低对比度图像。对比度拉伸可以扩展灰度级范围，使得图像的灰度级尽可能覆盖整个理想范围。分段线性变换是典型的对比度拉伸方案。

def LF(y1, y2, img):
    k = (y2[1] - y1[1]) / (y2[0] - y1[0])
    b = y1[1] - k * y1[0]
    y = k * img + b
    return np.clip(y, 0, 255)

def SLT(y1, y2, img):
    result = np.zeros_like(img, dtype=np.float32)
    
    a1 = img <= y1[0]
    a2 = (img > y1[0]) & (img < y2[0])
    a3 = img >= y2[0]

    result[a1] = 0
    result[a2] = LF(y1, y2, img[a2])
    result[a3] = 255
    
    return np.uint8(result)


if __name__ == '__main__':
    
    y1 = (np.min(image_gray), 0)
    y2 = (np.max(image_gray), 255)   # 适应性更强的分段点选择
    
    transformed_img = SLT(y1, y2, image_gray)

    plt.rcParams["font.family"] = "Times New Roman"
    plt.figure(figsize=(10, 7), dpi=300)
    plt.subplot(1, 2, 1)
    plt.title("Original Image", fontsize=16)
    plt.axis('off')
    plt.imshow(image_gray, cmap='gray', vmin=0, vmax=255)

    plt.subplot(1, 2, 2)
    plt.title("SLT Image", fontsize=16)
    plt.axis('off')
    plt.imshow(transformed_img, cmap='gray', vmin=0, vmax=255)

    plt.tight_layout()
    plt.show()