1. 第一节
1.1 一个不断添加噪音的逆向过程
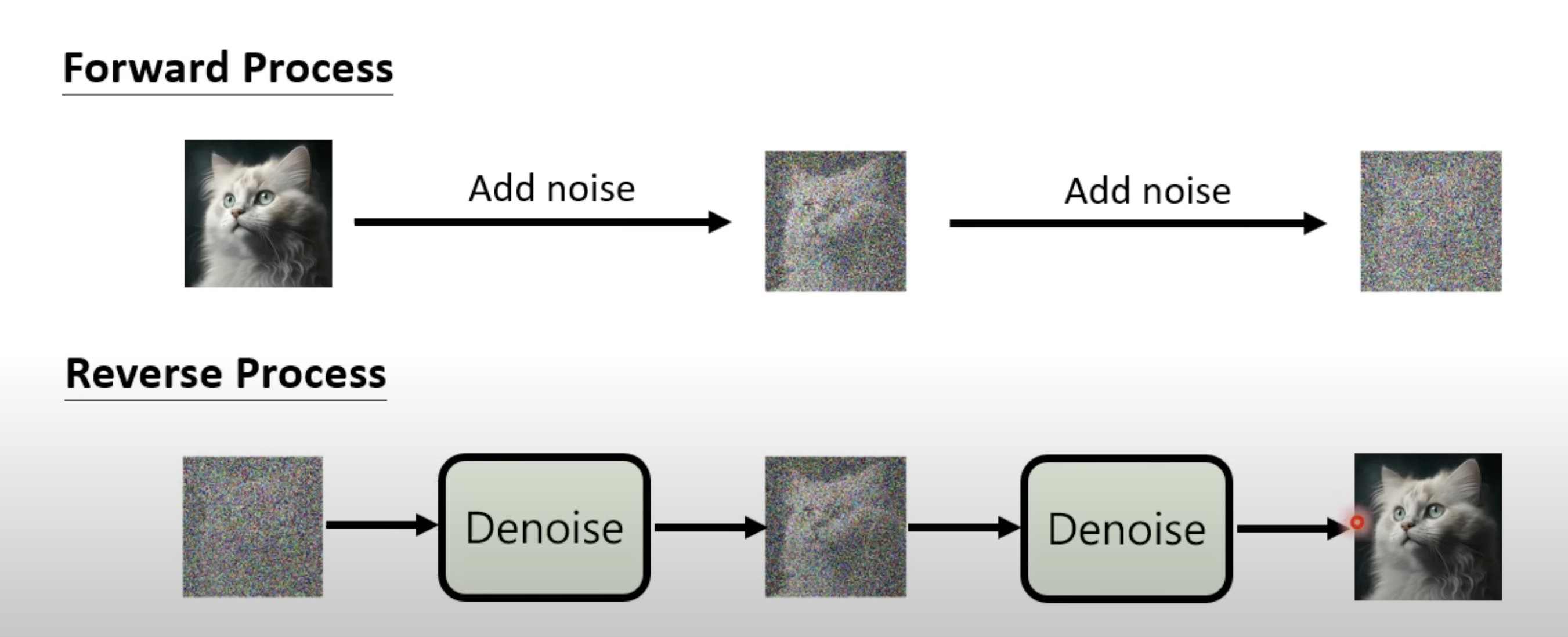
1.2 与 VAE 的区别和联系
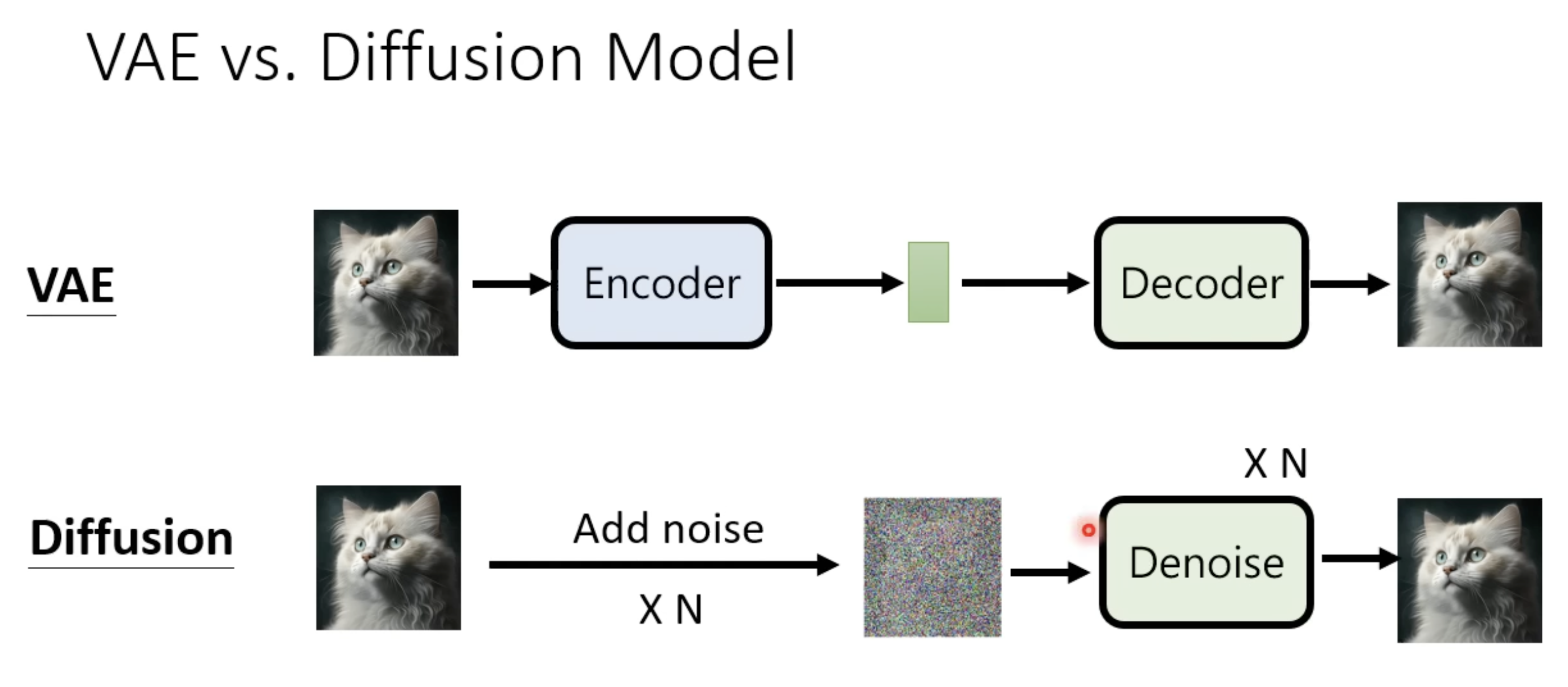
1.3 Diffusion 的训练原理

先产生一张 Noise Image,是通过 t 来选生成的;然后把选取的 t 和这张 noise Imgae 都输入到 Noise predictor 里面,得到预测的噪声,然后和真是的噪声作对比,得到损失。
1.4 Diffusion 的推理原理

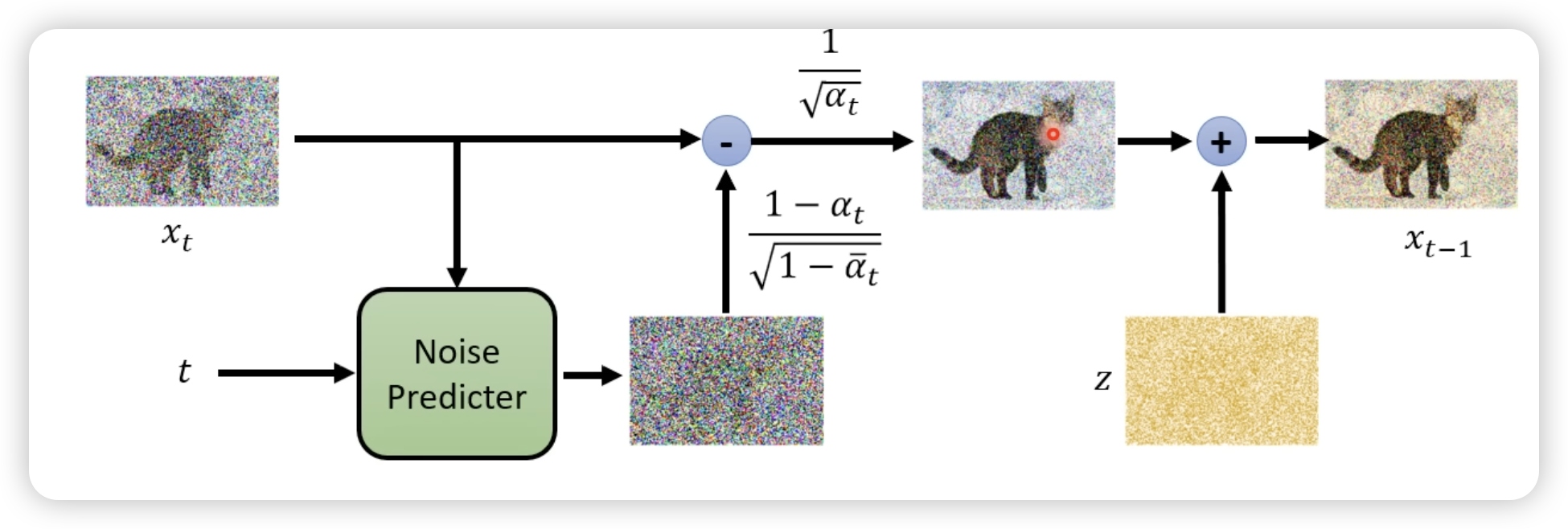
2. 第二节
2.1 生成模型的目标
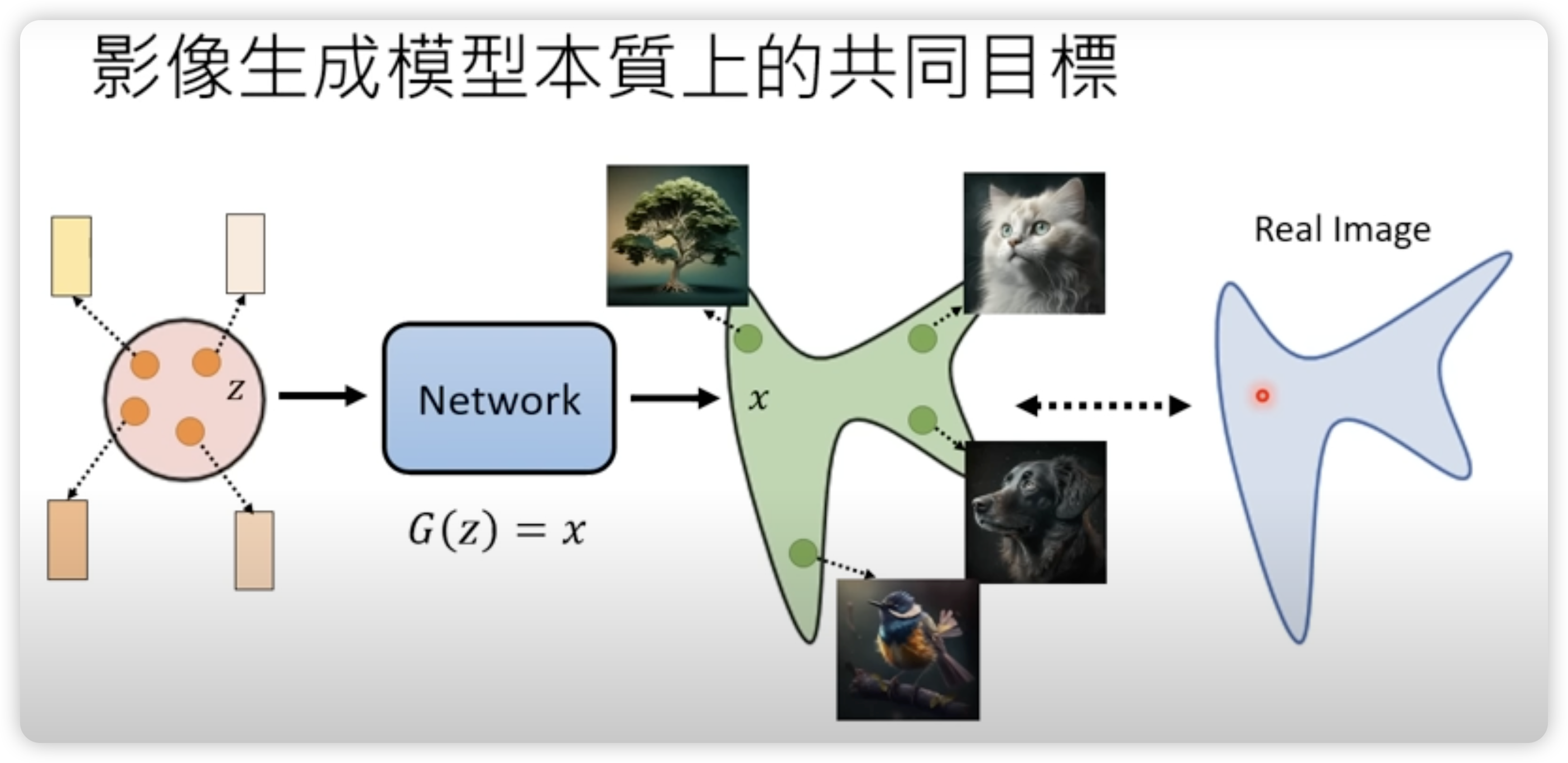
2.2 参数学习的目标
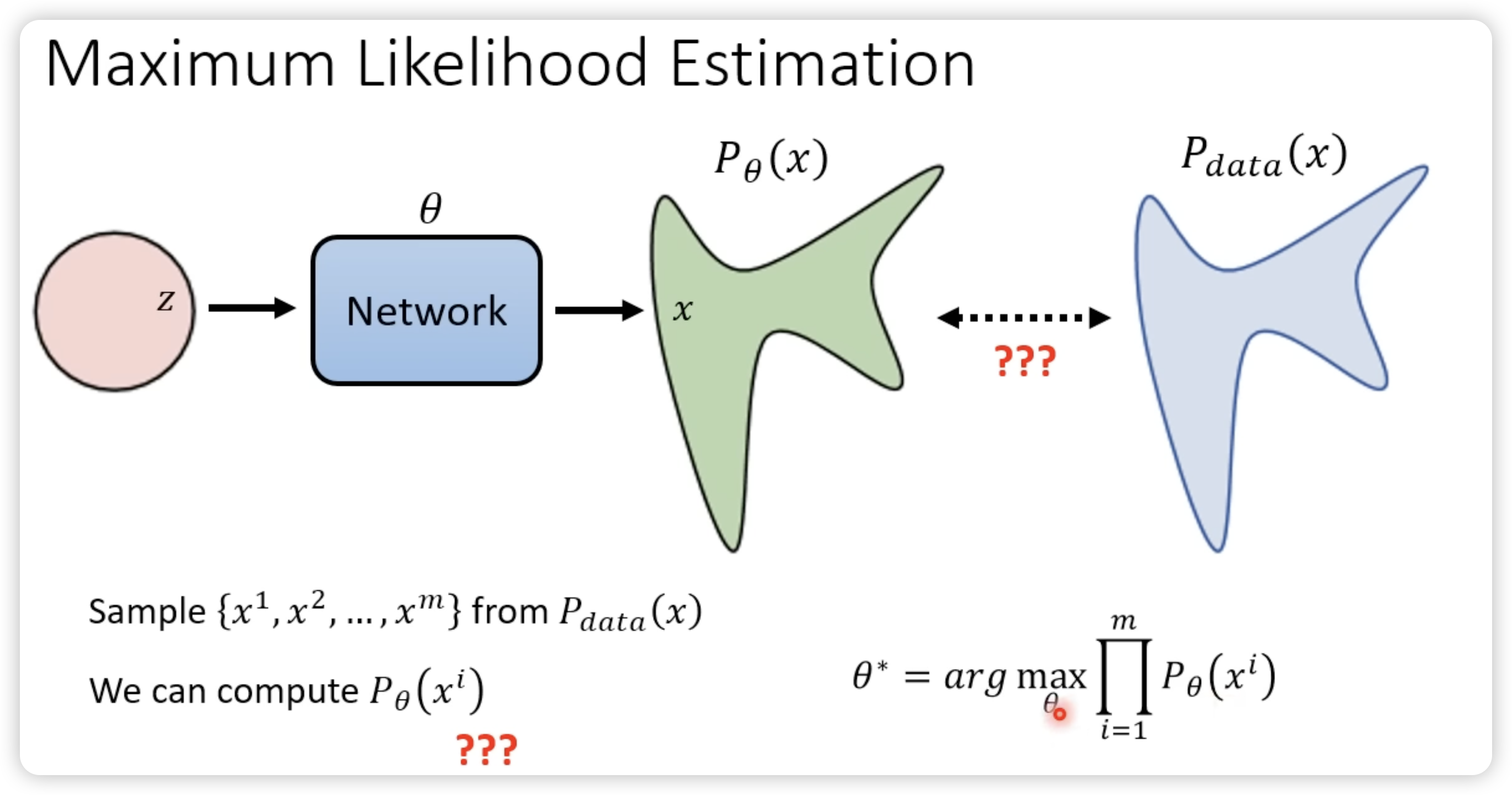
说白了就是,要找到一组参数,使得产生 x1,x2,…xm 的概率成绩越大越好。
优化公式推导:乘积——>积分

3. 第三节 DDPM
3.1 前向过程原理(Forward process)
参考学习 zhihu
参考学习 better
对于原始数据 x 0 x_0 x0~ q ( x 0 ) q(x_0) q(x0), 总共包含 T 步的扩散过程的每一步都是对上一步得到的数据 x t − 1 x_{t-1} xt−1按照如下方式增加高斯噪音:
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(x_t|x_{t-1}) = N(x_t;\sqrt{1-\beta_{t}}x_{t-1},\beta_{t}I) q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)
通过马尔科夫链+重参数技巧可以得到 x t x_t xt与 x 0 x_0 x0的直接关系
q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) q(x_t|x_0) = N(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_{t})I) q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)
其中 α t = 1 − β t \alpha_t = 1-\beta_t αt=1−βt 和 α ˉ t = ∏ i = 1 a i \bar\alpha_{t}=\prod_{i=1}{a_{i}} αˉt=∏i=1ai
这个特性很重要,可以看成
x
t
x_{t}
xt是原始数据
x
0
x_{0}
x0和随机噪音的线性组合.
α
ˉ
t
\sqrt{\bar\alpha_t}
αˉt和
(
1
−
α
ˉ
t
)
(1-\bar\alpha_{t})
(1−αˉt)是组合系数,被称为 signal*rate 和 noise_rate. 然后就可以基于
α
ˉ
∗
t
\bar\alpha*{t}
αˉ∗t 而不是
β
t
\beta_{t}
βt 来定义 noise schedule. 比如直接将
α
ˉ
t
\bar\alpha_{t}
αˉt 设定为接近 0 的值,那么就可以保证得到最终的
x
T
x_T
xT近似为一个随机噪音.

3.2 反向过程 (reverse process)
对于反向过程,其实就是一个去噪的过程,如果我们知道反向过程的每一步的真实分布
q
(
x
t
−
1
∣
x
t
)
q({x_{t-1}|x_{t}})
q(xt−1∣xt),那么从一个随机噪音
x
T
x_T
xT~N(0,1)开始,逐渐去噪就能得到一个真实的样本,即生成数据的过程.
反向过程也定义为一个马尔科夫链,只不过是由一系列的神经网络参数的高斯分布来组成.
在去除参数的过程中,我们需要用 x t x_t xt去预测 x t − 1 x_{t-1} xt−1. 采用贝叶斯公式去计算后验概率
P ( x t − 1 ∣ x t ) = P ( x t − 1 x t ) P ( x t ) = P ( x t ∣ x t − 1 ) P ( x t − 1 ) P ( x t ) P\left(x_{t-1} \mid x_t\right)=\frac{P\left(x_{t-1} x_t\right)}{P\left(x_t\right)}=\frac{P\left(x_t \mid x_{t-1}\right) P\left(x_{t-1}\right)}{P\left(x_t\right)} P(xt−1∣xt)=P(xt)P(xt−1xt)=P(xt)P(xt∣xt−1)P(xt−1)
然后由于原图 x 0 x_0 x0已知,进行公式改写:
P ( x t − 1 ∣ x t , x 0 ) = P ( x t ∣ x t − 1 , x 0 ) P ( x t − 1 ∣ x 0 ) P ( x t ∣ x 0 ) P\left(x_{t-1} \mid x_t, x_0\right)=\frac{P\left(x_t \mid x_{t-1}, x_0\right) P\left(x_{t-1} \mid x_0\right)}{P\left(x_t \mid x_0\right)} P(xt−1∣xt,x0)=P(xt∣x0)P(xt∣xt−1,x0)P(xt−1∣x0)
等式右边部分都变成先验概率,我们由前向加噪过程即可对公式进行改写,依据为
x
t
=
α
t
‾
x
0
+
1
−
α
t
‾
ϵ
x_t=\sqrt{\overline{\alpha_t}} x_0+\sqrt{1-\overline{\alpha_t}} \epsilon
xt=αtx0+1−αtϵ 和 $xt=\sqrt{1-\beta_t} x{t-1}+\sqrt{\beta_t} \epsilon $ 可以得到:
P ( x t − 1 ∣ x t , x 0 ) = N ( α t x t − 1 , 1 − α t ) N ( α t − 1 x 0 , 1 − α t − 1 − ) N ( α t ‾ x 0 , 1 − α t ‾ ) P\left(x_{t-1} \mid x_t, x_0\right)=\frac{N\left(\sqrt{\alpha_t} x_{t-1}, 1-\alpha_t\right) N\left(\sqrt{\alpha_{t-1}} x_0, 1-\alpha_{t-1}^{-}\right)}{N\left(\sqrt{\overline{\alpha_t}} x_0, 1-\overline{\alpha_t}\right)} P(xt−1∣xt,x0)=N(αtx0,1−αt)N(αtxt−1,1−αt)N(αt−1x0,1−αt−1−)
最后通过一系列 替换以及正态分布的性质,可以得到最终的结果.
P ( x t − 1 ∣ x t ) = N ( 1 α t ( x t − 1 − α t 1 − α t ‾ ϵ ) , ( 1 − α t ) ( 1 − α t − 1 − ) 1 − α t ‾ ) P\left(x_{t-1} \mid x_t\right)=N\left(\frac{1}{\sqrt{\alpha_t}}\left(x_t-\frac{1-\alpha_t}{\sqrt{1-\overline{\alpha_t}}} \epsilon\right), \frac{\left(1-\alpha_t\right)\left(1-\alpha_{t-1}^{-}\right)}{1-\overline{\alpha_t}}\right) P(xt−1∣xt)=N(αt1(xt−1−αt1−αtϵ),1−αt(1−αt)(1−αt−1−))
但是, ϵ \epsilon ϵ的具体的值我们并不知道, 因此我们需要去训练一个网络去预测噪声,也就是 李宏毅提到的 noise predictor.
4. 第四节 DDIM
DDPM 的缺陷在于,推理速度过慢,因为其本身是一个马尔科夫链的过程,无法进行跳跃预测,即无法通过 x t x_t xt直接去预测 x t − 2 x_{t-2} xt−2,于是就有了 DDIM 的出现. 无需重新训练 DDPM,只需要对采样器进行修改即可.
P ( x t − 1 ∣ x t , x 0 ) ∼ N ( ( α t − 1 − − 1 − α t − 1 − − σ 2 1 − α t ‾ α t ‾ ) x 0 + ( 1 − α t − 1 − − σ 2 1 − α t ‾ ) x t , σ 2 ) ∼ N ( α t − 1 − x 0 + 1 − α t − 1 − − σ 2 x t − α t x 0 1 − α t ‾ , σ 2 ) \begin{aligned} & P\left(x_{t-1} \mid x_t, x_0\right) \sim N\left(\left(\sqrt{\alpha_{t-1}^{-}}-\frac{\sqrt{1-\alpha_{t-1}^{-}-\sigma^2}}{\sqrt{1-\overline{\alpha_t}}} \sqrt{\overline{\alpha_t}}\right) x_0+\left(\frac{\sqrt{1-\alpha_{t-1}^{-}-\sigma^2}}{\sqrt{1-\overline{\alpha_t}}}\right) x_t, \sigma^2\right) \\ & \sim N\left(\sqrt{\alpha_{t-1}^{-}} x_0+\sqrt{1-\alpha_{t-1}^{-}-\sigma^2} \frac{x_t-\sqrt{\alpha_t} x_0}{\sqrt{1-\overline{\alpha_t}}}, \sigma^2\right) \end{aligned} P(xt−1∣xt,x0)∼N αt−1−−1−αt1−αt−1−−σ2αt x0+ 1−αt1−αt−1−−σ2 xt,σ2 ∼N(αt−1−x0+1−αt−1−−σ21−αtxt−αtx0,σ2)
采用与反向去噪同样的原理,将上述公式的
x
0
x_0
x0
进行替换,这里采用
ϵ
t
\epsilon_t
ϵt
是因为前文已经说明过采用的是模型预测的正态分布
x prev = α prev − ( x t − 1 − α t ‾ ϵ t α t ‾ ) + 1 − α prev − − σ 2 ϵ t + σ 2 ϵ x_{\text {prev }}=\sqrt{\alpha_{\text {prev }}^{-}}\left(\frac{x_t-\sqrt{1-\overline{\alpha_t}} \epsilon_t}{\sqrt{\overline{\alpha_t}}}\right)+\sqrt{1-\alpha_{\text {prev }}^{-}-\sigma^2} \epsilon_t+\sigma^2 \epsilon xprev =αprev −(αtxt−1−αtϵt)+1−αprev −−σ2ϵt+σ2ϵ
其中 x t x_t xt和 x p r e v x_{prev} xprev可以相隔多个迭代步数.
5. 总结
5.1 DDPM 公式
定义:
x t = α t x t − 1 + 1 − α t ϵ ϵ ∼ N ( 0 , 1 ) \begin{gathered} x_t=\sqrt{\alpha_t} x_{t-1}+\sqrt{1-\alpha_t} \epsilon \\ \epsilon \sim N(0,1) \end{gathered} xt=αtxt−1+1−αtϵϵ∼N(0,1)
经过推导得到 x 0 x_0 x0和 x t x_t xt
x t = α t ‾ x 0 + 1 − α t ‾ ϵ x 0 = x t − 1 − α t ‾ ϵ α t ‾ \begin{gathered} x_t=\sqrt{\overline{\alpha_t}} x_0+\sqrt{1-\overline{\alpha_t}} \epsilon \\ x_0=\frac{x_t-\sqrt{1-\overline{\alpha_t}} \epsilon}{\sqrt{\overline{\alpha_t}}} \end{gathered} xt=αtx0+1−αtϵx0=αtxt−1−αtϵ
进一步得到后验概率:
P ( x t − 1 ∣ x t ) = N ( 1 α t ( x t − 1 − α t 1 − α t ˉ ϵ ) , ( 1 − α t ) ( 1 − α t − 1 − ) 1 − α t ˉ ) P(x_{t-1}|x_t)=N(\frac1{\sqrt{\alpha_t}}(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha_t}}}\epsilon),\frac{(1-\alpha_t)(1-\alpha_{t-1}^-)}{1-\bar{\alpha_t}}) P(xt−1∣xt)=N(αt1(xt−1−αtˉ1−αtϵ),1−αtˉ(1−αt)(1−αt−1−))
其中的 ϵ 由模型提供 \text{其中的}\epsilon\text{由模型提供} 其中的ϵ由模型提供
5.2 DDIM 公式
DDIM 只修改了采样器,所以只需要重新定义后验概率即可
x p r e v = α p r e v ‾ ( x t − 1 − α t ϵ t α t ) + 1 − α p r e v ‾ − σ 2 ϵ t + σ 2 ϵ ϵ t = x t − α t x 0 1 − α ˉ t x 0 = x t − 1 − α ˉ t ϵ t α ˉ t \begin{aligned}x_{prev}&=\sqrt{\alpha_{\overline{prev}}}(\frac{x_t-\sqrt{1-\alpha_t}\epsilon_t}{\sqrt{\alpha_t}})+\sqrt{1-\alpha_{\overline{prev}}-\sigma^2}\epsilon_t+\sigma^2\epsilon\\\\\epsilon_t&=\frac{x_t-\sqrt{\alpha_t}x_0}{\sqrt{1-\bar{\alpha}_t}}\\\\x_0&=\frac{x_t-\sqrt{1-\bar{\alpha}_t}\epsilon_t}{\sqrt{\bar{\alpha}_t}}\end{aligned} xprevϵtx0=αprev(αtxt−1−αtϵt)+1−αprev−σ2ϵt+σ2ϵ=1−αˉtxt−αtx0=αˉtxt−1−αˉtϵt
其中的 ϵ t 由模型提供, σ 的值可以为0, x p r e v , x t 中间可以差多个间隔 \text{其中的}\epsilon_t\text{由模型提供,}\sigma\text{的值可以为0,}x_{prev},x_t\text{中间可以差多个间隔} 其中的ϵt由模型提供,σ的值可以为0,xprev,xt中间可以差多个间隔






















 1690
1690

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








