算法思路:用图中每一个点进行放缩,即图中每一个顶点与其他顶点的距离可通过另外的顶点进行缩短,则缩短,直至图中所有顶点完成放缩。
#include<iostream>
using namespace std;
int a[101][101],n;
void Floyd(){
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
if(a[i][j]>a[i][k]+a[k][j]){
a[i][j]=a[i][k]+a[k][j]; //放缩
}
}
}
int main(){
int u,v,k,m,c=0,o,e;
cout<<"请输入顶点个数"<<endl;
cin>>n;
cout<<"请输入图的边数"<<endl;
cin>>m;
for(int i=1;i<=n;i++) //初始化邻接矩阵
for(int j=1;j<=n;j++){
if(i==j)
a[i][j]=0;
else
a[i][j]=999;
}
cout<<"请构造图"<<endl;
while(c<m){
cin>>u>>v>>k;
a[u][v]=k;
a[v][u]=k;
c++;
}
cout<<"请输入起点编号"<<endl;
cin>>o;
cout<<"请输入终点编号"<<endl;
cin>>e;
Floyd();
cout<<"顶点"<<o<<"与顶点"<<e<<"的最短距离为"<<a[o][e];
return 0;
}
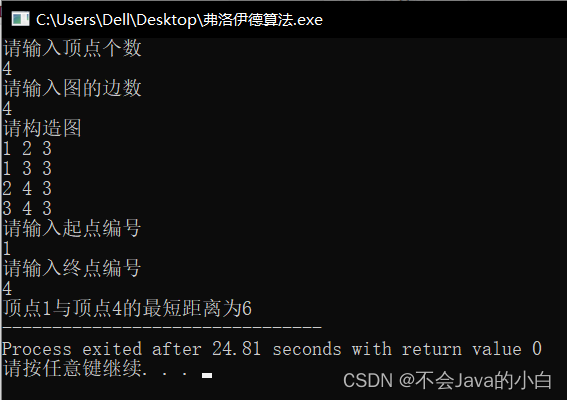




 本文介绍了一种基于Floyd算法的求解图中两点间最短路径的方法,通过更新邻接矩阵来逐步缩短距离直到找到最优路径。
本文介绍了一种基于Floyd算法的求解图中两点间最短路径的方法,通过更新邻接矩阵来逐步缩短距离直到找到最优路径。
















 1151
1151

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








