最短路径算法

原创已于 2025-07-07 16:22:14 修改 · 1.7k 阅读

33 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2024-02-12 22:17:24 首次发布

数据结构专栏收录该内容

33 篇文章

订阅专栏

部署运行你感兴趣的模型镜像

1. Dijkstra算法

在正数权重的有向图中求解某个源点到其余各个顶点的最短路径一般可以采用迪杰斯特拉算法（Dijkstra算法）。

1.1 适用场景

单源最短路径
权重都为正

该算法为什么权重必须为正?
Dijkstra算法要求权重都为正的原因在于其贪心策略和松弛操作的性质。以下是具体原因：
1.贪心策略
Dijkstra算法每次选择当前最短路径的节点进行扩展，假设从该节点到其他节点的路径不会更短。如果存在负权重，这一假设可能不成立，因为后续的负权重可能使路径变得更短，导致算法无法正确找到最短路径。
2.松弛操作
算法通过松弛操作更新路径长度，假设路径长度只会减少或保持不变。负权重可能导致路径长度反复减少，使得算法无法在有限步骤内确定最短路径。
3.节点处理顺序
Dijkstra算法按路径长度递增的顺序处理节点，一旦节点被处理，其最短路径不再更新。负权重可能导致已处理节点的路径长度需要重新计算，破坏算法的正确性。
4.负权环问题
如果图中存在负权环，路径长度可以无限减少，Dijkstra算法无法处理这种情况。
总结
Dijkstra算法依赖权重为正的假设，确保每次选择的最短路径是全局最优的。若存在负权重，算法可能失效。对于包含负权重的图，应使用Bellman-Ford等算法。

1.2 伪代码

在这里插入图片描述
这里需要详细说明参数，v表示第一个顶点，D[i]表示从v到各个顶点vi的最短路径长度。

1.3 示例

问题描述： 计算节点0到节点4的最短路径，图路径如下：
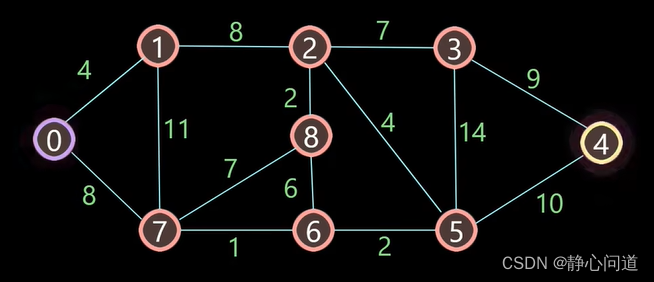
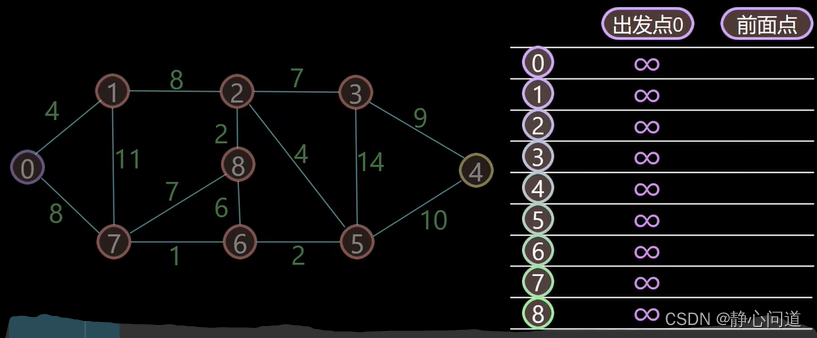
在这里插入图片描述
step1: 采用二维表记录0点到其他节点的距离，第一列距离初始化为 $\infty$ ，第二列记录到达每个节点时，该节点前面的点，主要用于最短路径回溯。

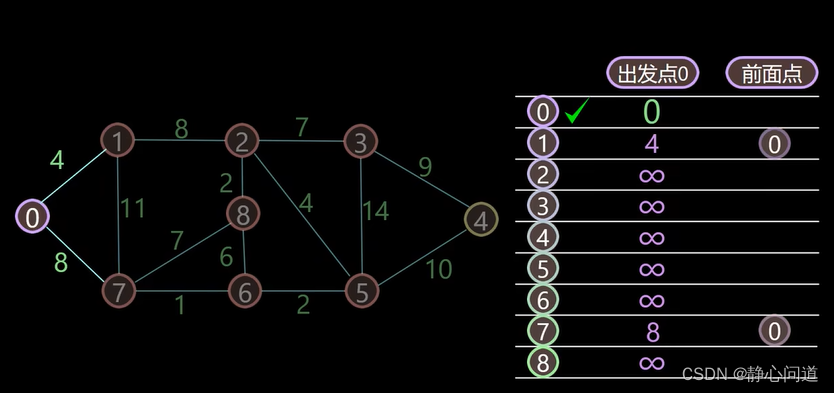
step2: 0到0的距离是0，为最优路径，标记为对勾，节点0到节点1、7的距离分别为4、8，节点1、7前面的点为节点0，所以在前面点填写0。
在这里插入图片描述
step3: 在未标记的点中选取最小值，最小值为4，对应的节点为1，将其标记为最优路径，标记为对勾，计算最小值节点1的邻居节点。

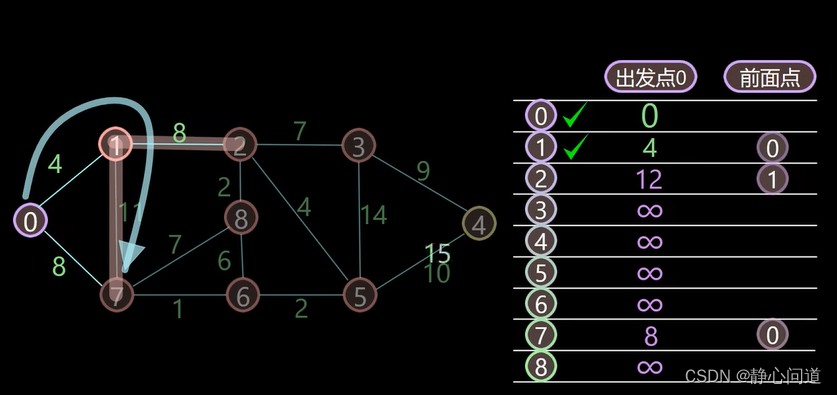
经过最小值节点1可以到达邻居节点2、7，到节点2的距离是 $4+8=12<\infty$ ，所以更新节点2的距离为12，到达节点2时，经过的前面节点为节点1。
经过最小值节点1到达节点7的距离 $4 + 11 = 15 > 8$ ，所以不更新节点7，节点7前面的节点仍为节点0。
step4: 在剩余未标记的点中选取最小值，最小值为8，对应的节点为7，将其标记为最优路径，标记为对勾，计算最小值节点7的邻居节点。
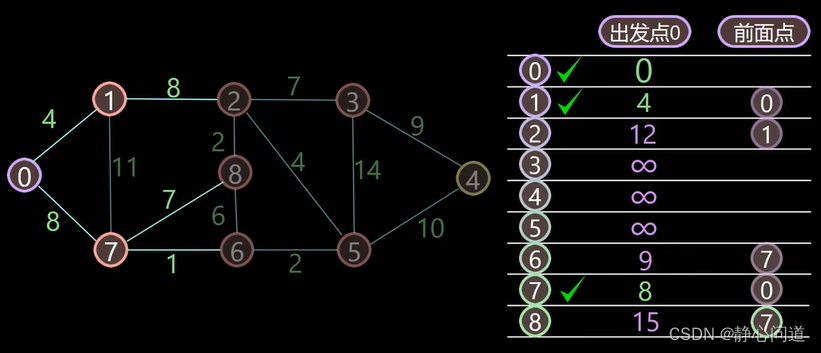
在这里插入图片描述
更新节点6、8，节点6的距离8(节点7的最短距离)+1=9和节点8的距离8(节点7的最短距离)+7=15，前面的节点都为7。以此类推，更新所有的节点。

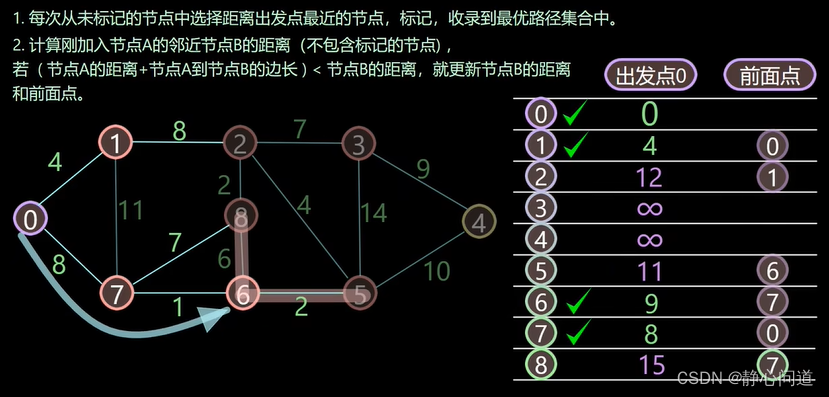
最后0到所有节点的最短近距离如下：

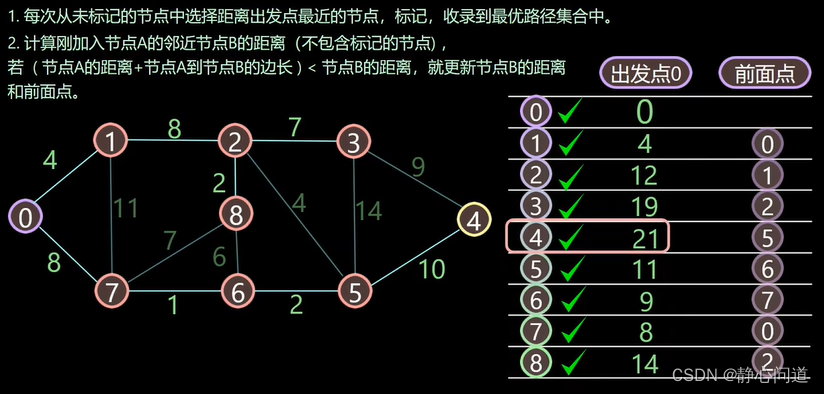
1.4 计算最短路径

节点0到节点4的最短距离为21，节点4的前面节点为节点5， $\rightarrow 4$ ，节点5前面的节点是节点6, $\rightarrow5$ ，节点6前面是节点7， $7\rightarrow6$ ，节点7前面是节点0， $0\rightarrow7$ ，综上所述，最短路径为： $\rightarrow 7 \rightarrow6 \rightarrow 5 \rightarrow 4$ ，距离为21。

1.5 Leetcode例子

https://leetcode.cn/problems/network-delay-time/solutions/909575/wang-luo-yan-chi-shi-jian-by-leetcode-so-6phc/

#include <iostream>
#include <vector>
#include <queue>
#include <limits>

using namespace std;

const int INF = numeric_limits<int>::max();

vector<int> dijkstra(const vector<vector<pair<int, int>>>& graph, int source) {
    int n = graph.size();
    vector<int> dist(n, INF);
    vector<bool> visited(n, false);
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
    
    dist[source] = 0;
    pq.push({0, source});
    
    while (!pq.empty()) {
        int u = pq.top().second;
        pq.pop();
        
        if (visited[u]) continue;
        visited[u] = true;
        
        for (auto& edge : graph[u]) {
            int v = edge.first;
            int weight = edge.second;
            if (dist[u] + weight < dist[v]) {
                dist[v] = dist[u] + weight;
                pq.push({dist[v], v});
            }
        }
    }
    
    return dist;
}

int main() {
    vector<vector<pair<int, int>>> graph = {
        {{1, 4}, {2, 2}},
        {{3, 3}},
        {{1, 1}, {3, 5}},
        {}
    };

    int source = 0;
    vector<int> distances = dijkstra(graph, source);

    cout << "Shortest distances from node " << source << ":" << endl;
    for (int i = 0; i < distances.size(); ++i) {
        cout << "Node " << i << ": " << distances[i] << endl;
    }

    return 0;
}

在这个示例中，我们定义了一个 dijkstra() 函数来执行 Dijkstra 算法。该函数接受一个邻接表表示的图和源节点作为输入，并返回从源节点到每个节点的最短路径距离。

1.6 输出最短路径

如果存在多条最短路径就输出多条最短路径

import heapq
from collections import defaultdict

def dijkstra(graph, start, end):
    # 优先队列，存储 (距离, 当前节点, 路径)
    pq = [(0, start, [start])]
    # 记录每个节点的最短距离
    shortest_distances = {start: 0}
    # 记录所有最短路径
    shortest_paths = defaultdict(list)

    while pq:
        current_dist, current_node, path = heapq.heappop(pq)

        # 如果当前节点是终点，记录路径
        if current_node == end:
            shortest_paths[current_dist].append(path)
            continue

        # 如果当前距离大于已知的最短距离，跳过
        if current_dist > shortest_distances.get(current_node, float('inf')):
            continue

        # 遍历邻居节点
        for neighbor, weight in graph[current_node].items():
            distance = current_dist + weight
            # 如果找到更短的路径
            if distance < shortest_distances.get(neighbor, float('inf')):
                shortest_distances[neighbor] = distance
                heapq.heappush(pq, (distance, neighbor, path + [neighbor]))
            # 如果找到等长的路径
            elif distance == shortest_distances.get(neighbor, float('inf')):
                heapq.heappush(pq, (distance, neighbor, path + [neighbor]))

    # 如果没有找到路径
    if not shortest_paths:
        return None, None

    # 获取最短距离
    min_distance = min(shortest_paths.keys())
    # 获取所有最短路径
    all_shortest_paths = shortest_paths[min_distance]

    return min_distance, all_shortest_paths

# 示例图
graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}

start = 'A'
end = 'D'

# 运行算法
distance, paths = dijkstra(graph, start, end)

# 输出结果
if distance is not None:
    print(f"最短距离: {distance}")
    print("所有最短路径:")
    for path in paths:
        print(" -> ".join(path))
else:
    print("没有找到路径")

2. Bellman-Ford算法

Bellman-ford算法适用于单源最短路径，图中边的权重可为负数即负权边，但不可以出现负权环。

2.1 适用场景

单源最短路径
边的权重可为负数即负权边
不可以出现负权环

2.2 伪代码

在这里插入图片描述

2.3 示例

step1: 初始图如下，箭头上的数字表示权重，括号内容含义为：（前面节点，距离），除去源点，其他点的初始距离为 $\infty$ 。 $\textcircled{1}-\textcircled{7}$ 表示边的编号。接下来，从节点0到节点n-1开始遍历。
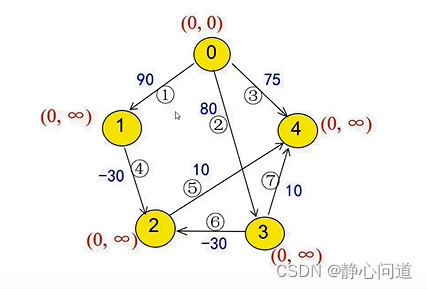
在这里插入图片描述
step2: 从节点0出发：更新所有节点的权重，节点 $\rightarrow 1$ 为90， $\rightarrow 4$ 为75， $\rightarrow 3$ 为80，它们的距离都小于 $\infty$ ，到达节点的上一个节点都是节点0，更新为（0，距离）。

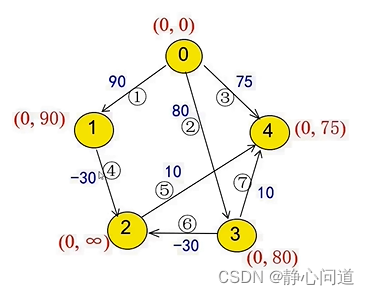
step3: 从节点1出发， $\rightarrow 1 \rightarrow 2$ 为 $90-30=60<\infty$ ，由于节点2上一个节点是节点1，所以标记为（1，60）。
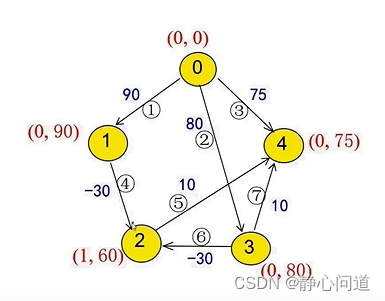
在这里插入图片描述
step3: 从节点2出发，60+10<75，节点4更新为（2，70）

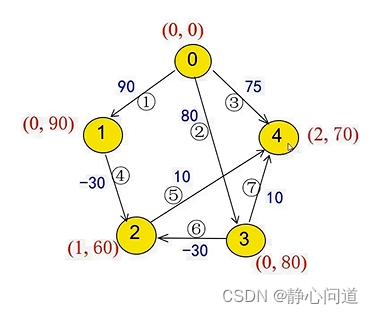
step4: 从节点3出发，80-30=50<60，更新节点2为（3，50）。80+10=90>70，无需更新节点4。

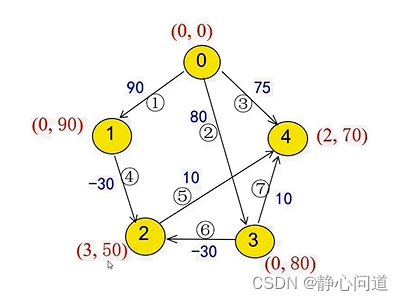
step4: 从节点4出发，不存在边，无需更新，完成第一遍所有的松弛操作。

step5: 进行第二轮遍历，由于节点 $\rightarrow 4$ 的和50+10=60<70，更新节点4为（2，60）。
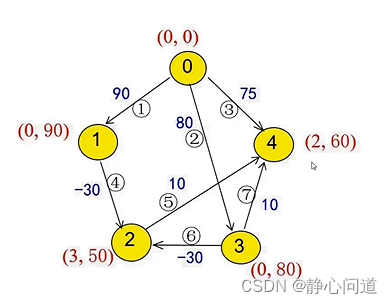
在这里插入图片描述

step6: 第三遍遍历没有任何松弛操作，且3<=n-1=4，说明不存在负权重的环，可以直接返回节点0到其他节点的距离。如果存在松弛操作，最多进行n-1轮遍历，如果第n轮还存在松弛操作，说明存在负权重的环。
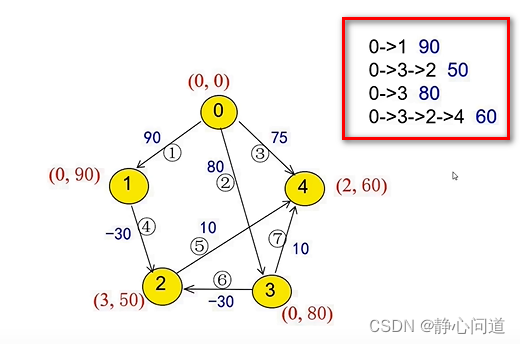
最短路径如下图红框所示：

2.4 计算最短路径

在这里插入图片描述

2.5 补充

如果存在负环，示例如下：
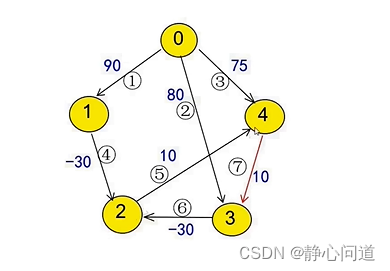
在这里插入图片描述
节点2、3、4存在负环，负环会导致无穷迭代。
第1遍遍历结果

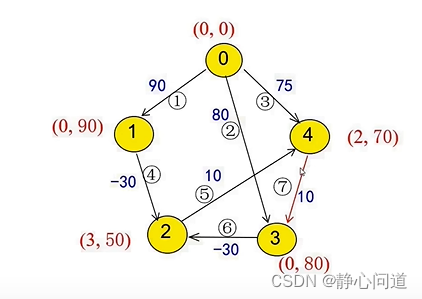
更新节点4为（2，60）

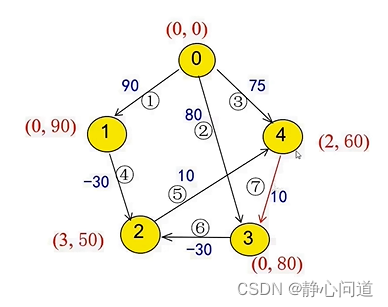
更新节点3为（4，70）

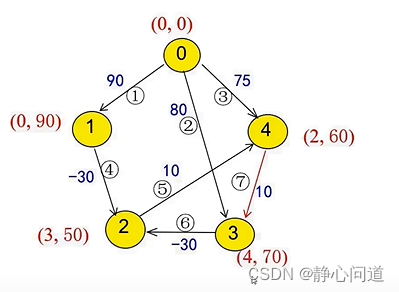
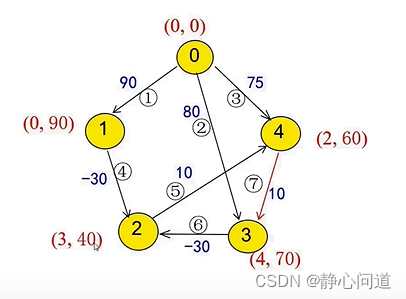
更新节点2为（3，40），以此类推，导致无穷迭代。

2.6 参考资料

Bellman-ford算法无向图

3 Floyd算法

Floyd算法是也称为弗洛伊德算法或插点法，是一种动态规划算法，求解多源最短路（多对多）的算法，即确定每个节点（起点）到其他节点（终点）的最短路。

3.1 适用场景

求解多源最短路(多对多)的算法
算法适用于有向图、无向图，允许边的权重为负，但是负边构成的回路（环）的权重之和不能为负（负环）

3.2 伪代码

在这里插入图片描述

//Floyd
//多源最短路
static int[][] g=new int[n+1][n+1];//邻接矩阵存图
static int[][][] dp=new int[n+1][n+1][n+1];
static void Floyed(){
	for(int k=0;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if(k==0){
					dp[k][i][j]=g[i][j];
				}else{
					dp[k][i][j]=Math.min(dp[k-1][i][j],dp[k-1][i][k]+dp[k-1][k][j]);
				}
				
			}
		}
	}
}

3.3 示例

step 1: 初始化邻接矩阵，节点编号从1开始
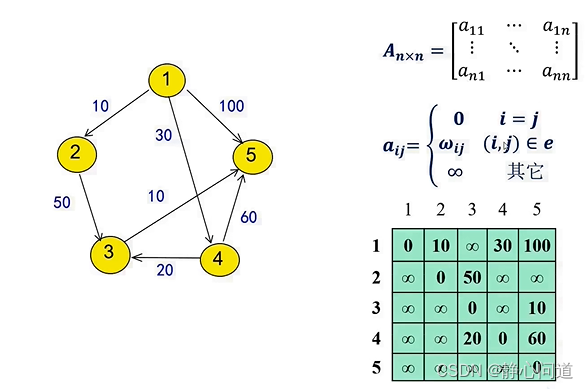
在这里插入图片描述
step 2: 每一轮选取中间节点，比较 $a_{ij}$ 和 $a_{ik}+a_{kj}$ 大小

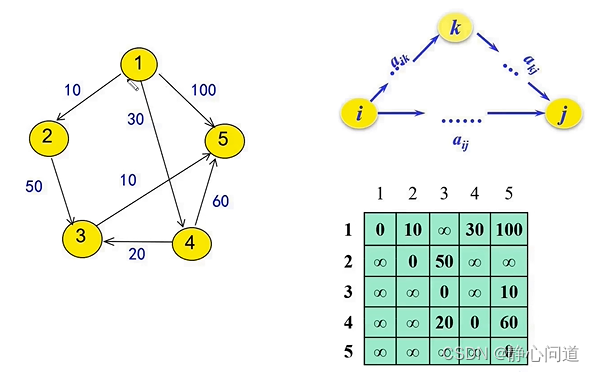
step 3: 采用两个矩阵存储，绿色矩阵存储源节点（src）和目标节点（dst）之间的距离，黄色矩阵存储dst节点前面的节点。0表示节点直达，不存在中间节点。注意：节点的编号是从1开始的，0标号不存在冲突。
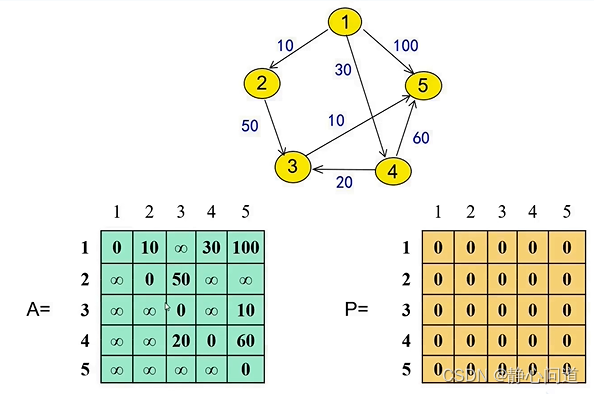
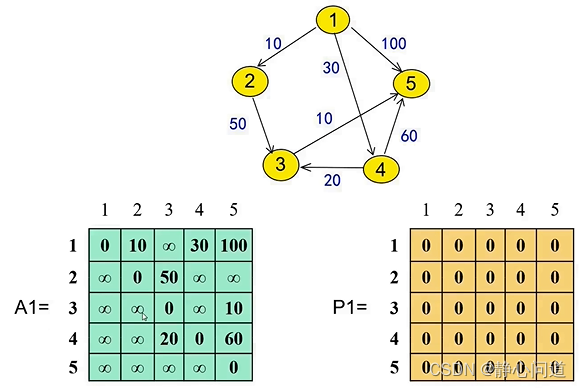
在这里插入图片描述
step 4: 从节点1作为中间节点开始遍历，主要关注 $a_{i1}$ 和 $a_{1j}$ 矩阵更新结果如下：

step 5: 从节点2作为中间节点开始遍历，主要关注 $a_{i2}$ 和 $a_{2j}$ 矩阵更新结果如下：

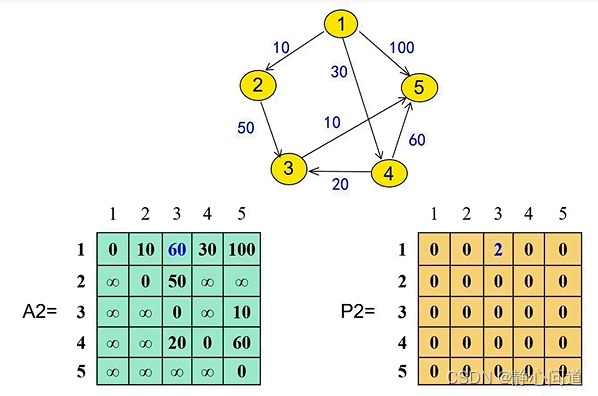
由于 $\lt \infty$ ，所以更新A2矩阵 $A [1] [3] = 60$ ，经过的节点为2，更新P2矩阵为 $P 2 [1] [3] = 2$ 。
step 6: 从节点3作为中间节点开始遍历，主要关注 $a_{i3}$ 和 $a_{3j}$ 矩阵更新结果如下：
在这里插入图片描述
由于 $A2[3][5]=60<\infty, A2[4][3] + A[3][5]=30<60$ , 所以在A3中更新 $A 3 [1] [5], A 3 [2] [5], A 3 [4] [5]$ , 在P3中更新对应的前置节点为3。
step 7: 从节点4作为中间节点开始遍历，主要关注 $a_{i4}$ 和 $a_{4j}$ 矩阵更新结果如下：
在这里插入图片描述
step 8: 从节点5作为中间节点开始遍历，主要关注 $a_{i5}$ 和 $a_{5j}$ 矩阵更新结果如下：

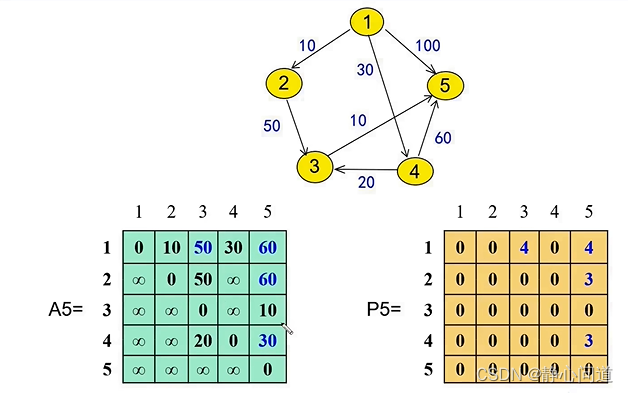
3.4 计算最短路径

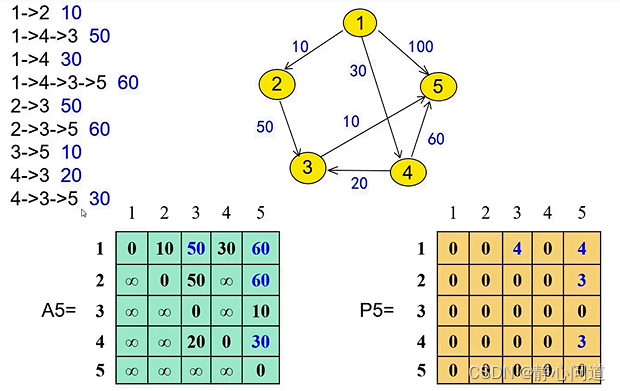
在这里插入图片描述

分析1： $1\rightarrow 2$
- 距离为 $A 5 [1] [2] = 10$
- 由于 $P 5 [1] [2] = 0$ , 表示节点2前面没有中间节点，属于直连的情况。
分析2： $1\rightarrow 5$
- 距离为 $A 5 [1] [5] = 60$ ,
- 由于 $P 5 [1] [5] = 4$ ，表示需要经过中间节点4， $1\rightarrow 4\rightarrow5$ 。
- 递归分析 $1\rightarrow 4$ ， $P 5 [1] [4] = 0$ , 表示节点4前面没有中间节点，属于直连的情况。
- 递归分析 $4\rightarrow 5$ ， $P 5 [4] [5] = 3$ ，表示需要经过中间节点3， $4\rightarrow 3\rightarrow5$ 。
- 递归分析 $4\rightarrow 3$ ， $P 5 [4] [3] = 0$ , 表示节点3前面没有中间节点，属于直连的情况。
- 递归分析 $3\rightarrow 5$ ， $P 5 [3] [5] = 0$ , 表示节点5前面没有中间节点，属于直连的情况。
- 回溯结果，最短路径最终为 $1\rightarrow4\rightarrow 3\rightarrow 5$ 。

4 SPFA 算法

SPFA 算法是 Bellman-Ford算法的队列优化算法的别称，通常用于求含负权边的单源最短路径，以及判负权环。SPFA 最坏情况下时间复杂度和朴素 Bellman-Ford 相同，为 O(VE)。

4.1 适用场景

单源最短路径
边的权重可为负数即负权边
不可以出现负权环

4.2 伪代码

在这里插入图片描述

4.3 示例

https://zhuanlan.zhihu.com/p/353019102

5 算法特点对比

5.1 Dijkstra 与Bellman-ford

（1）Dijkstra为贪心算法，Bellmon-Ford算法不是贪心算法
（2）Dijkstra在有负权的情况下无法工作，Bellmon-Ford算法允许有负权。
（3）Bellmon-Ford算法可以用来判定是否有负权环。
（4）从计算复杂度角度分析，单节点算法首选Dijkstra算法的，它的计算复杂度为 $O(n^2)$ ，Bellman-ford时间复杂度为O(m*n)，n表示有n个点，m表示有m条边。

Bellman-ford算法的时间复杂度是O(N*M)，这个时间复杂度貌似比Dijkstra算法还要高，我们还可以对其进行优化。在实际操作中，Bellman-ford算法经常会未达到n-1轮松弛前就已经算出最短路，因此我们可以判断第k轮是否进行更新,如果不进行更新了，则可以提前跳出循环。
Bellman-ford算法的另一种优化在文中已经有所提示：在每实施一次松弛操作后，就会有一些顶点已经求其最短路。此后这些顶点的最短路的估计值就会一直保持不变，不在受后序松弛操作的影响，但是每次还需要判断是否需要松弛。这就启发我们：每次仅对最短路估计值发生变化了的顶点的所有出边执行松弛操作。详情请看Bellman-ford的队列优化-SPAF。

5.2 Floyd与Dijkstra

Floyd算法和Dijkstra算法都是用于解决图论中最短路径问题的算法，但它们在适用范围、计算复杂度、算法原理等方面存在差异：

（1）适用范围：
Floyd算法：适用于求解图中任意两个顶点之间的最短路径，可以处理带负权边的图。
Dijkstra算法：适用于求解图中一个源点到其他所有点的最短路径，不能处理负权边的图。
（2）计算复杂度：
Floyd算法：时间复杂度为 $O(n^3)$ ，适用于边数较少的稠密图。
Dijkstra算法：时间复杂度为 $O(n^2)$ ，适用于边数较多的稀疏图。
（3）算法原理：
Floyd算法：是一种动态规划算法，通过定义一个距离矩阵，并更新这个矩阵，逐步找到图中任意两点之间的最短路径。
Dijkstra算法：是一种贪心算法，每次找到距离源点最近的顶点，并更新与之相连的顶点的最短路径，直到所有顶点都被遍历过一次或找到终点。
（4）算法特点：
Floyd算法：可以处理负权边，但时间复杂度较高。
Dijkstra算法：只适用于无负权边的图，时间复杂度较低。
SPFA 算法：与bfs算法比较，复杂度相对稳定。但在稠密图中复杂度比迪杰斯特拉算法差。

参考资料：
https://blog.youkuaiyun.com/weixin_41806489/article/details/126852955
https://www.bilibili.com/video/BV1zz4y1m7Nq
https://www.bilibili.com/video/BV18a4y1A7gv
https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247488007&idx=1&sn=9d0dcfdf475168d26a5a4bd6fcd3505d&chksm=fd9cb918caeb300e1c8844583db5c5318a89e60d8d552747ff8c2256910d32acd9013c93058f&token=754098973&lang=zh_CN#rd

您可能感兴趣的与本文相关的镜像