高级0-1背包问题——动态规划

最新推荐文章于 2024-09-17 23:07:02 发布

jacob2359

最新推荐文章于 2024-09-17 23:07:02 发布

阅读量422

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构与算法

本文链接：https://blog.youkuaiyun.com/jacob__lei/article/details/89503679

高级0-1背包问题：已知n个物品，每种物品对应有重量weight和价值value两个属性，给定一个背包可以装入物品的最大重量为maxWeight，求满足最大重量限制的情况下，背包中装入物品的总价值最大是多少？
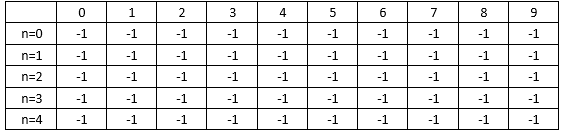
实例：总共有5种物品，即n=5，每个物品的重量为weights=[ 2，2，4，6，3]，对应价值为values=[3, 4, 8, 9, 6]，最大重量maxWeight=9，求背包中可装如物品的总价值最大是多少？
- 如下表所示，表中行表示的第几个物品，表中的列表示物品的重量，由于背包的最大重量maxWeight=9，因此，该背包总共有0~9种重量的可能，表中的数据项表示价值，记为curValue，初始状态下curValue=-1。初始状态如下表所示:
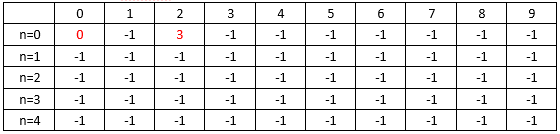
- 当第0号物品决策完之后，即不放入背包或放入背包，如果不放入背包，则在curWeight=0的列curValue=0，如果放入背包，即在curWeight=2的列curValue=3，改变表中的对应状态：
- 对于第1号物品：
  - 将物品(curWeight=2, curValue=4)不放入背包时：根据n=0的状态集合可以得到n=1的状态集合，如下所示：