简单0-1背包问题——动态规划_请利用动态规划求解0-1背包问题。0-1背包问题是说,已知n个物品,每个物品的重量和-优快云博客

本文链接：https://blog.youkuaiyun.com/jacob__lei/article/details/89480931

动态规划最经典问题：0-1背包问题，但是经典的0-1背包问题给每个物品赋予两种属性（重量、价值），往往初次看此问题时难度较大。为了便于理解，先从经典的0-1背包问题提取一种属性进行分析（重量），题目如下：

简单0-1背包问题：已知n个物品，每种物品对应有一个重量weight，给定一个背包可以装入物品的最大重量为maxWeight，求满足最大重量限制的情况下，背包中物品总重量的最大值是多少？
首先通过一个例子来分析简单0-1背包问题。假设总共有5种物品，即n=5，每个物品的重量为weights=[ 2，2，4，6，3]，最大重量maxWeight=9。如下表所示，表中的行表示第几个物品，表中的列表示物品的重量，记为curWeight，由于背包的最大重量maxWeight=9，因此，该背包总共有0~9种重量的可能。
- 初始状态如下表所示：
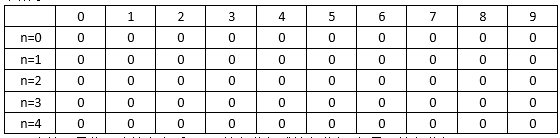
- 当第0号物品决策完之后，即将0号物品不放入背包或将0号物品放入背包，如果不放入背包，即curWeight=0，如果放入背包，即curWeight=2，改变表中的对应状态：
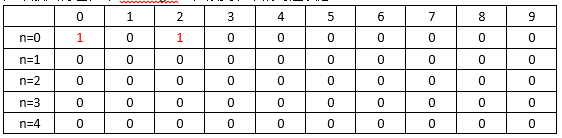
- 当第1号物品决策完之后，即将1号物品不放入背包或将1号物品放入背包，如果不放入背包，基于n=0时的状态集合，该背包中的重量有两种可能，即curWeight=0或curWeight=2，如果放入背包，基于n=0时的状态集合，该背包中的重量有两种可能，即curWeight=2或curWight=4，综上，1号物品决策完之后，背包中的重量总共有三种可能，即curWeight=0、curWeight=2或curWight=4。改变表中的对应状态：
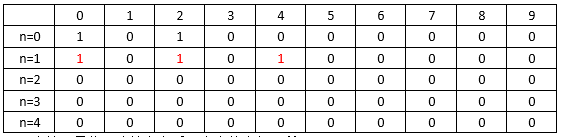
- 当第2号物品决策完之后，表中状态如下所示：
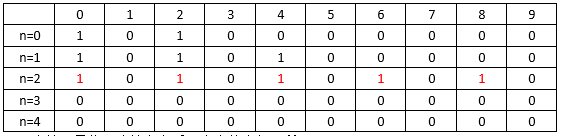
- 当第3号物品决策完之后，表中状态如下所示：
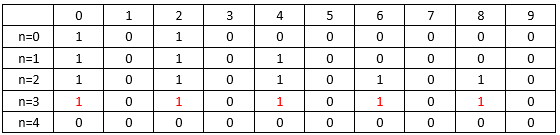
- 当第4号物品决策完之后，表中状态如下所示：
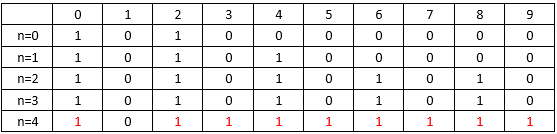
- 根据上表可知，当前背包下物品总重量的最大值为9.

将上述过程转化为代码为：

/**
 * 背包中物品总重量的最大值
 * @param weight 每个物品的重量数组
 * @param n 物品的个数
 * @param maxWight 背包可承受的最大重量
 * @return 背包中物品总重量的最大值
 */
public int getMaxWeightInPackage(int[] weight, int n, int maxWight){
    int res = 0;
    Boolean[][] state = new Boolean[n][maxWight+1]; // 先申请状态数组，即上面的表格的初始化状态
    
    // 对第0行进行特殊处理，手动标记
    state[0][0] = true;             //  将第0号物品不放入背包
    state[0][weight[0]] = true;     // 将第0号物品放入背包

    // 依次对剩下的物品进行决策
    for (int i=1; i<n; i++){
        // 将第i号物品不放入背包
        for (int j=0; j<=maxWight; j++){
            if ( state[i-1][j] != null && state[i-1][j] == true){
                state[i][j] = state[i-1][j];
            }
        }

        // 将第i号物品放入背包
        for (int j=0; j<= (maxWight-weight[i]); j++){
            if(state[i-1][j] != null && state[i-1][j] == true)
                state[i][j+weight[i]] = true;
        }
    }

    // 在最后一行从后向前遍历
    for (int i=maxWight; i>=0; i--){
        if(state[n-1][i] != null && state[n-1][i] == true){
            res = i;
            break;
        }
    }
    return res;
}

从上述实例可知，对于每个物品都有两种决策方案，要么放入背包，要么不放入背包。将整个过程分解成n个部分，对于每个部分都有两种决策方案，当每个物品决策完之后（放入背包或不放入背包）背包中的重量有多种情况，也就是说达到多种不同的情况。把每一层重复的状态合并，只记录不同的状态，然后基于上一层的状态集合，来推导下一层的状态集合。当所有部分决策完之后，即可得到最终的状态集合，从状态集合中可以得到该背包中最大的重量。
实际上，这就是动态规划解决问题的基本思路。将问题分解为多个阶段，每个阶段对应一个决策。我们记录每一个阶段可达的状态集合（去掉重复的部分），然后通过当前的状态集合来推到下一阶段的状态集合，动态地往前推进。
从上述代码可知，该问题的时间复杂度为O(n*weight)，其中n为物品的个数，maxWeight为背包可承载的最大重量，该问题的空间复杂度为O(n*weight)，其中n为物品的个数，maxWeight为背包可承载的最大重量

优化：事实上，只需要申请weight+1的一维数组即可解决这个问题。代码如下：

public int getMaxWeightInPackage2(int[] weight, int n, int maxWight) {
    int res = 0;
    Boolean[] state = new Boolean[maxWight+1]; // 先申请状态数组

    // 对第0行进行特殊处理，手动标记
    state[0] = true;             //  将第0号物品不放入背包
    state[weight[0]] = true;     // 将第0号武平放入背包

    // 依次对剩下的物品进行决策
    for (int i = 1; i < n; i++) {
        for (int j=maxWight-weight[i]; j>=0; j--){  // 把第i个物品放入背包中
            if (state[j] != null && state[j] == true)
                state[j+weight[i]] = true;
        }
    }

    // 在最后一行从后向前遍历
    for (int i=maxWight; i>=0; i--){
        if(state[i] != null && state[i] == true){
            res = i;
            break;
        }
    }

    return res;
}