Wikipedia 上关于Ford-Fulkerson算法的描述如下
Algorithm Ford-Fulkerson
-
Inputs
Graph
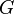 with flow capacity
with flow capacity  , a source node
, a source node  , and a sink node
, and a sink node 
-
Output
A flow
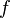 from
from  to
to  which is a maximum
which is a maximum
-
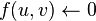 for all edges
for all edges 
- While there is a path
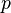 from
from  to
to  in
in 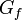 , such that
, such that 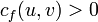 for all edges
for all edges 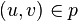 :
:
- Find
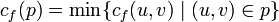
- For each edge
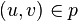
-
 (Send flow along the path
)
(Send flow along the path
) -
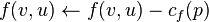 (The flow might be "returned" later
)
(The flow might be "returned" later
)
-
- Find
-
虽然算法貌似很简单,但是算法正确性的证明过程确实比较困难,由于本人才疏学浅,所以证明过程虽然看了好多便,现在仍然不甚明了,今天太晚了,明天继续搞,先把今晚用残量图实现的Ford-Fulkerson算法贴出来,注释比较详细。
package com.FeeLang; public class FordFulkerson { public static void main(String[] args){ // int[][] net = new int[4][4]; // net[0][1] = 1000; // net[0][2] = 1000; // net[1][2] = 1; // net[1][3] = 1000; // net[2][3] = 1000; int nodes = 6; int[][] capacity = new int[nodes][nodes]; capacity[0][1] = 7; capacity[0][2] = 6; capacity[1][3] = 4; capacity[1][4] = 2; capacity[2][3] = 2; capacity[2][4] = 3; capacity[3][5] = 9; capacity[4][5] = 5; FordFulkerson maxFlow = new FordFulkerson(capacity, nodes); int max = maxFlow.getMaxFlow(0, 5); System.out.println(max); } public FordFulkerson(int[][] net, int nodes){ this.net = net; this.nodes = nodes; pre = new int[nodes]; visited = new boolean[nodes]; } public int getMaxFlow(int s, int t){ //initial the residual capacities residual = net; int maxFlow = 0; while (true){ for (int i = 0; i < nodes; i++) visited[i] = false; //initial residual capacities getPath(s, t); if (!visited[t]){ // not find a path from s to t break; } //get the min capacity of the path int min = Integer.MAX_VALUE; for (int i = t; i > s; i = pre[i]){ min = Math.min(min, residual[pre[i]][i]); } //send min units of flow to the path. //Update residual capacities for (int i = t; i > s; i = pre[i]){ residual[pre[i]][i] -= min; residual[i][pre[i]] += min; } maxFlow += min; } return maxFlow; } //search a path from s to t public void getPath(int s, int t){ visited[s] = true; for (int i = 0; i < nodes; i++){ if (!visited[i] && residual[s][i] > 0){ visited[i] = true; pre[i] = s; getPath(i, t); } } } private boolean[] visited; private int[][] net; private int[][] residual; private int[] pre; private int nodes;






 本文介绍了一种基于残量图实现的最大流算法——Ford-Fulkerson算法,并提供了一个具体的Java实现示例。该算法通过不断寻找源节点到汇节点的增广路径来逐步增加流值,直至无法找到新的增广路径为止。
本文介绍了一种基于残量图实现的最大流算法——Ford-Fulkerson算法,并提供了一个具体的Java实现示例。该算法通过不断寻找源节点到汇节点的增广路径来逐步增加流值,直至无法找到新的增广路径为止。
















 184
184

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








