数学中,重心坐标是由单形(如三角形或四面体等)顶点定义的坐标。重心坐标是齐次坐标的一种。
设 v1, ..., vn 是向量空间 V 中一个单形的顶点,如果 V 中某点 p 满足,
那么我们称系数 (λ1, ..., λn) 是 p 关于 v1, ..., vn 的重心坐标。这些顶点自己的坐标分别是 (1, 0, 0, ..., 0), (0, 1, 0, ..., 0), ..., (0, 0, 0, ..., 1)。重心坐标不是惟一的:对任何不等于零的 k,(k λ1, ..., k λn) 也是 p 的重心坐标。但总可以取坐标满足 λ1 + ...+ λn = 1,称为正规化坐标。注意到定义式在仿射变换下不变,故重心坐标具有仿射不变性。
如果坐标分量都非负,则 p 在 v1, ..., vn 的凸包内部,即由这些顶点组成的单形包含 p。我们设想如果有质量 λ1, ..., λn 分别位于单形的顶点,那么质量中心就是 p。这是术语“重心”的起源,1827年由奥古斯特·费迪南德·莫比乌斯最初引入。
三角形的重心坐标
在三角形情形,重心坐标也叫面积坐AP:PC 标,因为 P 点关于三角形 ABC 的重心坐标和三角形 PBC, PCA 及 PAB 的(有向)面积成比例,证明如下(图如右)。
我们用黑体小写字母表示对应点的向量,比如三角形 ABC 顶点为  和
和  ,P 点为
,P 点为  等。设 PBC, PCA 及 PAB 面积之比为
等。设 PBC, PCA 及 PAB 面积之比为 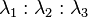 且 λ1 + λ2 + λ3 = 1,设射线 AP 与 BC 交于 D,则
且 λ1 + λ2 + λ3 = 1,设射线 AP 与 BC 交于 D,则
-
BD:DC = λ2:λ3, 从而

- AP:PD = (λ2 + λ3):λ1,故
-
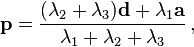
-

所以,(λ1,λ2,λ3) 就是 P 的重心坐标。
坐标变换
给定三角形平面一点 P,我们将这一点的面积坐标 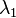 ,
, 和
和 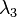 用笛卡尔坐标表示出来。
用笛卡尔坐标表示出来。
利用笛卡尔坐标中的三角形面积公式:
我们可得:
类似地有 λ2,λ3,注意 ABC 构成一个三角形,上式的分母不可能为 0。
反过来则简单得多:
-
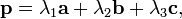 故
故
- xp = λ1xa + λ2xb + λ3xc, 和
- yp = λ1ya + λ2yb + λ3yc.
判断一点的位置
因重心坐标是笛卡尔坐标的一个线性变换,从而它们在边和三角形区域之间的变化是线性的。如果点在三角形内部,那么所有重心坐标属于开区间 (0,1);如果一点在三角形的边上,至少有一个面积坐标 λ1...3 为 0,其余分量位于闭区间 [0,1]。如果有某个坐标小于 0,则位于三角形外部,具体分布可参考上图。
应用
面积坐标在涉及到三角形子区域的工程学问题时特别有用,经常可以化简解析积分求值,高斯积分法表也常以面积坐标的形式给出。
考虑由顶点  ,
,  和
和  定义的三角形 T,任何在三角形内部的点
定义的三角形 T,任何在三角形内部的点  都能写成顶点的加权和:
都能写成顶点的加权和:
这里 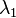 、
、 和
和 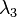 是面积坐标。注意到
是面积坐标。注意到 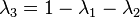 。 从而,函数 f 在 T 上的积分为:
。 从而,函数 f 在 T 上的积分为:
这里 S 是三角形 T 的面积。注意上式具有线性插值的形式。
重心坐标提供了一种非结构网格上函数插值的方法,假设函数值在所有网格的顶点上已知。如果 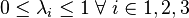 ,则点
,则点  位于三角形内部或边界上。我们取 f 的插值为
位于三角形内部或边界上。我们取 f 的插值为
这个线性插值是自动正规的因为 λ1 + λ2 + λ3 = 1。
四面体的重心坐标
重心坐标容易推广到三维空间。3 维单形即四面体,具有四个三角形面和四个顶点。
完全类似于三角形,四面体  的顶点
的顶点  的重心坐标为 (1,0,0,0),
的重心坐标为 (1,0,0,0),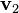 为 (0,1,0,0),如是等等。
为 (0,1,0,0),如是等等。
点  的笛卡尔坐标和为关于四面体
的笛卡尔坐标和为关于四面体  的重心坐标的关系:
的重心坐标的关系:
这里 Vol(V1V2V3V4) 为  组成的四面体的体积,类似于三角形也可以用笛卡尔坐标的一个行列式表示出来。
组成的四面体的体积,类似于三角形也可以用笛卡尔坐标的一个行列式表示出来。
3 维重心坐标和 2 维一样,可以确定一点是否位于四面体内部,也能对四面体网格上函数插值。因为利用重心坐标可以极大地简化 3 维插值,四面体网格经常用于有限元分析。
参考文献
- Bradley, Christopher J.(2007年).The Algebra of Geometry: Cartesian, Areal and Projective Co-ordinates.Bath:Highperception.ISBN 978-1-906338-00-8.
- Eric W. Weisstein, Areal Coordinates, MathWorld.
外部链接
- 重心坐标:一个奇怪的运用(解“三杯子问题”)位于 cut-the-knot
- 齐次重心坐标在平面欧几里得几何中的运用




 本文介绍了数学中的重心坐标概念,包括其定义、性质及其在三角形和四面体中的应用。通过具体的坐标变换公式,展示了如何使用重心坐标进行点位置判断和函数插值。
本文介绍了数学中的重心坐标概念,包括其定义、性质及其在三角形和四面体中的应用。通过具体的坐标变换公式,展示了如何使用重心坐标进行点位置判断和函数插值。




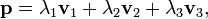


















 1192
1192

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








