科普 | 三分钟看懂「Sinc效应」

数模转换器（DAC）作为数字信号到模拟信号转换的必备环节,广泛应用于信号产生、仪器仪表、无线通信中。由于 DAC 器件在实现上采用了零阶保持器,使其幅频特性上固有的存在 Sinc效应。

在窄带系统中，Sinc效应的影响可忽略，但在宽带调制信号生成或是雷达对抗应用中，DAC器件的Sinc效应已成为设计者不得不面对的一个问题。

1.Sinc效应的产生机理

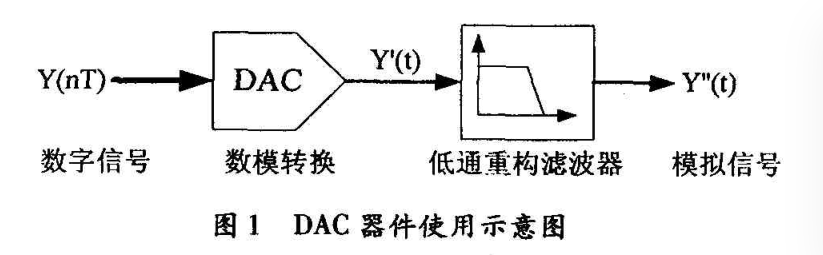
图中是DAC器件使用示意图，Y(nT)为转换前的数字信号、Y(t)为经DAC转换后的模拟信号、(t)为低通滤波后的模拟信号。下图对信号的时域波形变化情况和对应的频谱特性进行了分析。

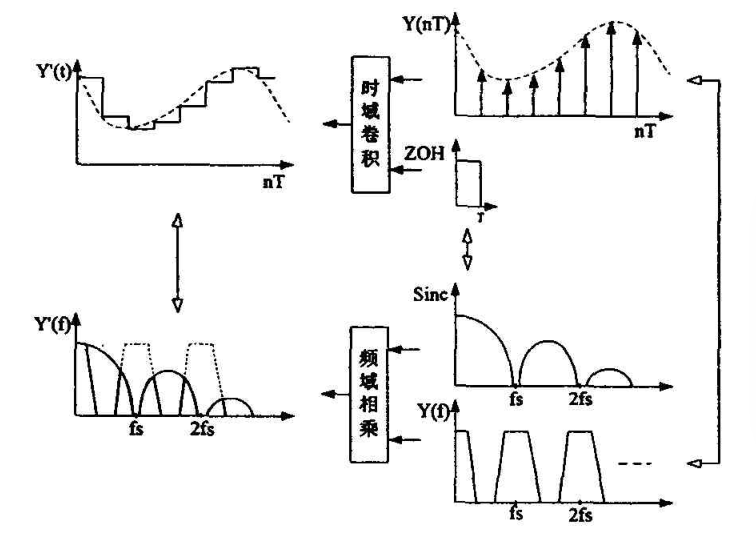
可以看出，由于DAC器件中采用了零阶保持器，当数字信号转换为模拟信号时会对其频谱产生Sinc镜像和衰落。

其中，数字信号频谱会以采样频率fs为周期无限重复，这些重复的频谱称为“镜像频率”或“混叠频率”。

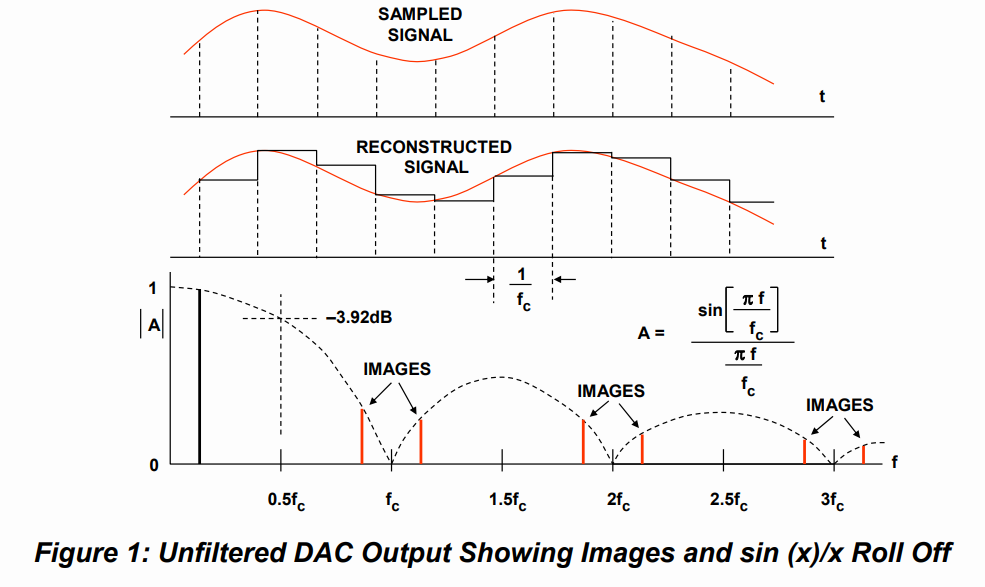
虽然Sinc函数的主瓣集中在奈奎斯特频率范围内，但其旁瓣仍然会包含镜像频率，尤其是在第二奈奎斯特区域的镜像。这些镜像频率会随着频率的增加而逐渐衰减，但无法完全消除。

2.Sinc效应的影响

镜像频率（或称为混叠频率）是采样和重建过程中不可避免的现象，它们会对信号处理系统产生多种不利影响。

1）信号失真

镜像频率会干扰原始信号的频谱，导致信号失真。具体表现为：

频谱污染：镜像频率会出现在原始信号频带内（尤其是当采样频率不足时），与原始信号的频谱重叠，从而掩盖或改变信号的真实特征。

幅度和相位失真：镜像频率的存在会导致信号的幅度和相位特性发生变化，影响信号的完整性。例如，在音频信号中，这可能导致声音失真或出现额外的噪声。

2. 降低信号质量

镜像频率的存在会降低信号的整体质量，尤其是在对信号质量要求较高的应用中。例如在无线通信或有线传输中，镜像频率可能会干扰相邻信道，降低信号的传输效率和可靠性。

3. 对后续处理的影响

镜像频率的存在会对后续的信号处理步骤产生负面影响。例如：

数字信号处理：在数字滤波或信号分析中，镜像频率可能会被误认为是信号的一部分，导致错误的分析结果。

4.限制系统性能

镜像频率的存在会限制系统的性能，尤其是在以下方面：

采样频率要求：为了避免镜像频率的干扰，采样频率必须足够高（根据奈奎斯特准则，至少是信号最高频率的两倍）。这可能增加系统的功耗和处理负担。

动态范围受限：镜像频率的干扰会降低系统的动态范围，影响信号的信噪比（SNR）和总谐波失真（THD）。

3.总结

Sinc效应作为DAC中不可忽视的非理想因素，既是信号保真的挑战，也是系统优化的突破口。

立思方基于软件综合射频理念开发IC8723综合射频系统，充分考虑了Sinc效应的影响，利用多种技术保证了信号的高真实性与高平坦度。

获取完整产品资料或预约真机演示，可扫描上方二维码直达产品专员⬇⬇⬇