干货 | 一文厘清信号分析中FFT频谱泄漏与加窗（文末附知识测验，快来挑战）

在数字信号处理领域，傅里叶变换在分析日常信号和排查信号问题中具有重要作用，其核心是将信号分解为不同幅度和频率的正弦波。

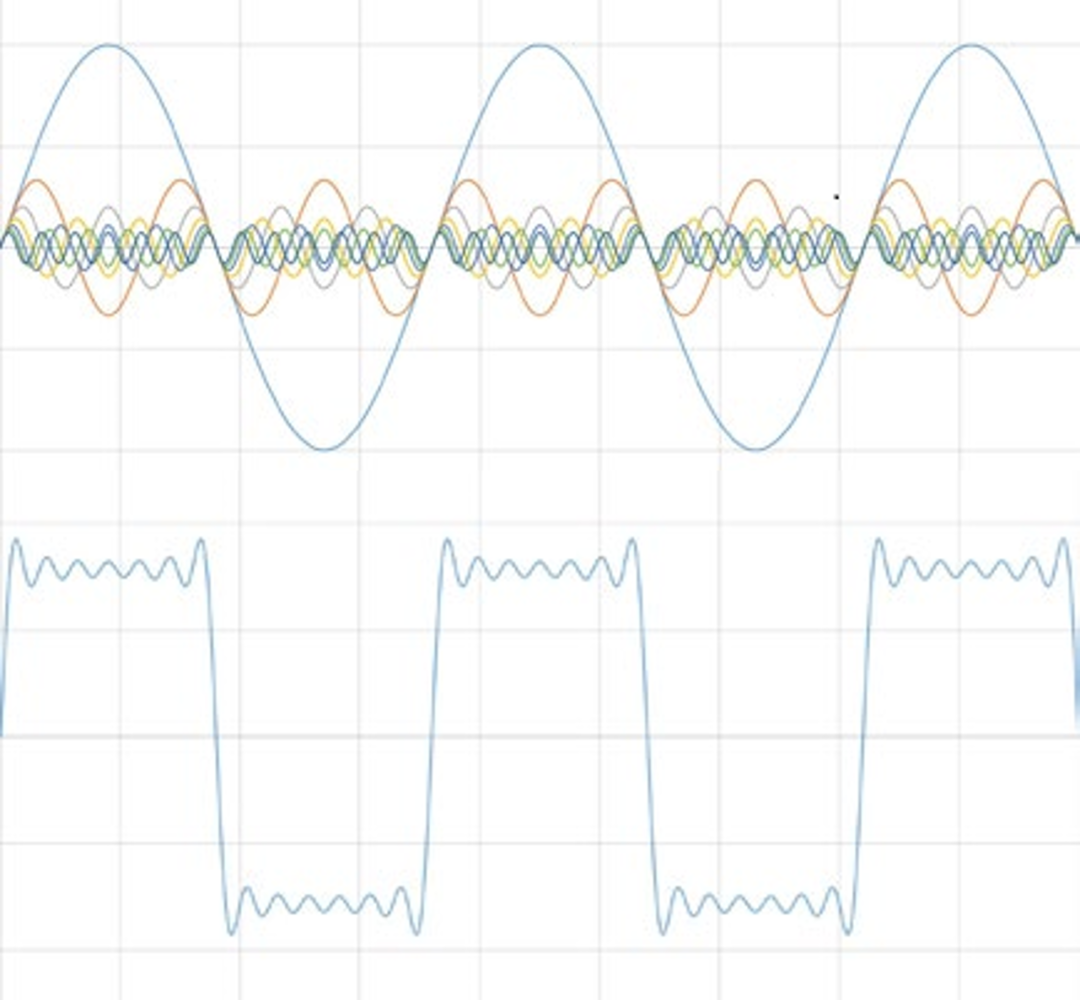
图：方波是正弦波的叠加

01

FFT：频谱泄漏

FFT默认假设被分析的信号在采样窗口内是周期性重复的，但在实际情况中，常常并不能测量到整数个周期，这时被测量信号就会被从周期中间切断，有限数据采样会使测量信号产生突变即产生信号的不连续性，这些不连续片段在FFT中显示为高频成分，这些频率可能远高于麦奎斯特频率，在0～采样率一半的频率区间内产生混叠，因此利用FFT获得的频率是一个被改变过的频率。如下图中可以看到，FFT变换后，其频谱在真实频点周围存在大量的杂散成分，且频点最大值有一定幅度的下降。

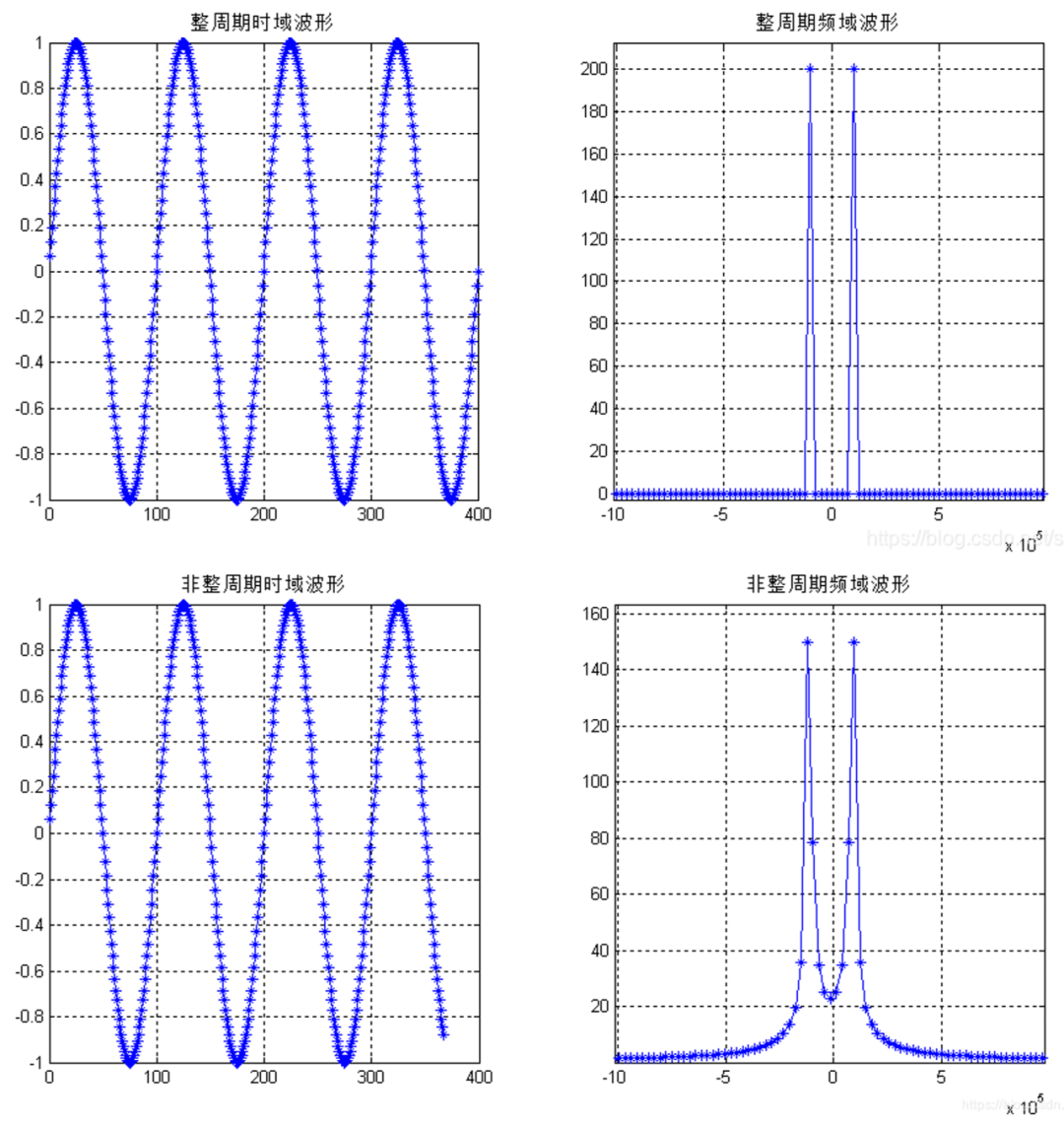
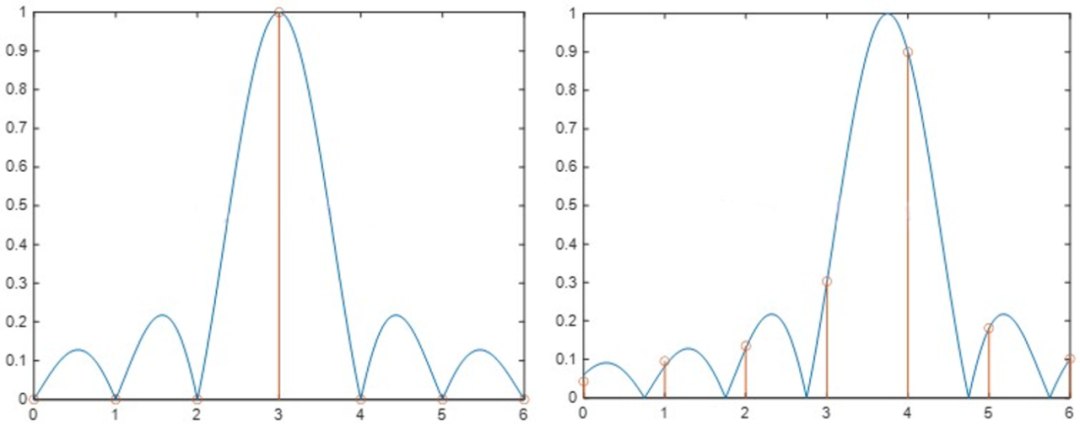
加之FFT本质上是对连续频域sinc函数在离散频率点上的等间隔采样，如果信号频率未精确对齐频率仓（非整周期截断）即采样频率与信号频率不同步，sinc函数的旁瓣也会在这些离散点上被采样，这就导致能量通过旁瓣泄漏到非目标频率，进而引发频谱泄漏。在数学中，时域信号的截断就相当于乘以一个突变的矩形函数，这种操作在频域中表现为与sinc函数（主瓣+旁瓣）的卷积。

02

加窗：降低旁瓣泄漏

综上可知，频谱泄漏与窗函数频谱的两侧旁瓣有关，如果两侧旁瓣的高度趋于零，而使能量相对集中在主瓣，就可以较为接近于真实的频谱。因此，为了减少频谱能量泄漏，可采用不同的截取函数对信号进行截断，截断函数称为窗函数，简称为窗。

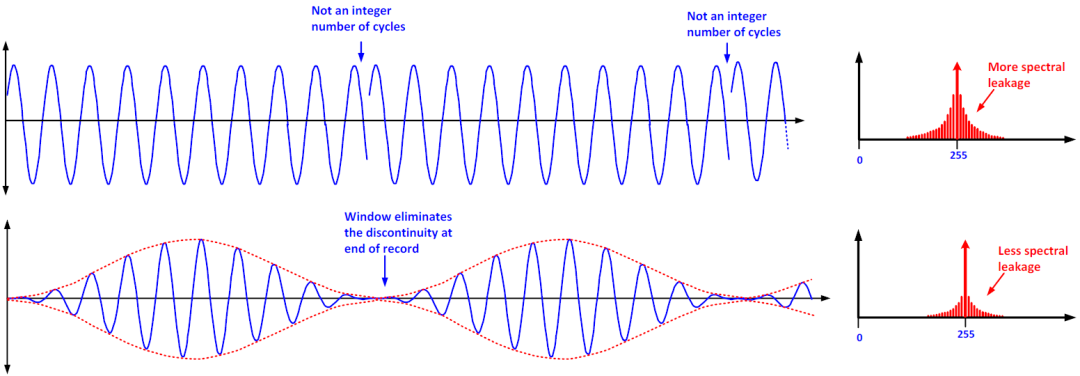
图：加窗后，消除采样波形中的不连续性

1）时域加窗

通常时域上加窗更为普遍，时域截断效应带来频谱泄漏，窗函数为了减小这个截断效应，被设计成一组加权系数w(n)。加窗在时域上表现的是点乘，因此在频域上则表现为卷积。卷积可以被看成是一个平滑的过程，相当于一组具有特定函数形状的滤波器，因此，原始信号中在某一频率点上的能量会结合滤波器的形状表现出来，从而减小泄漏。

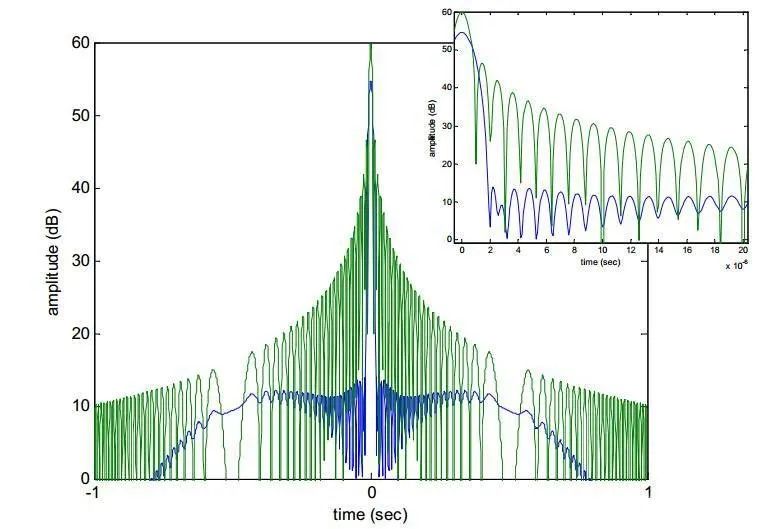
图：对LFM的时域加窗会导致主瓣变宽而旁瓣得到明显降低，并且最大幅值也有所降低。

  2）频域加窗

频域加窗在频域上表现为点乘，这是为了减小脉冲压缩后时域的距离向旁瓣，而对匹配滤波器的频率响应加窗。我们知道线性调频脉冲的频率响应近似为矩形，对其乘以窗函数可得到修正后的频率响应。

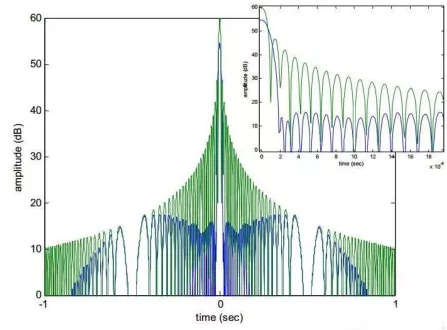
图：修正后的频率响应不再与发射的LFM信号匹配，输出峰值和信噪比都会有一定减小

03

窗函数：有何不同？如何选择？

不同的窗函数对信号频谱的影响是不一样的，这主要是因为不同的窗函数产生泄漏的大小不一样，频率分辨能力也不一样。为了不影响截短序列的相位响应，通常需要窗函数保持线性相位，以下是几种常用的窗函数及频率响应：

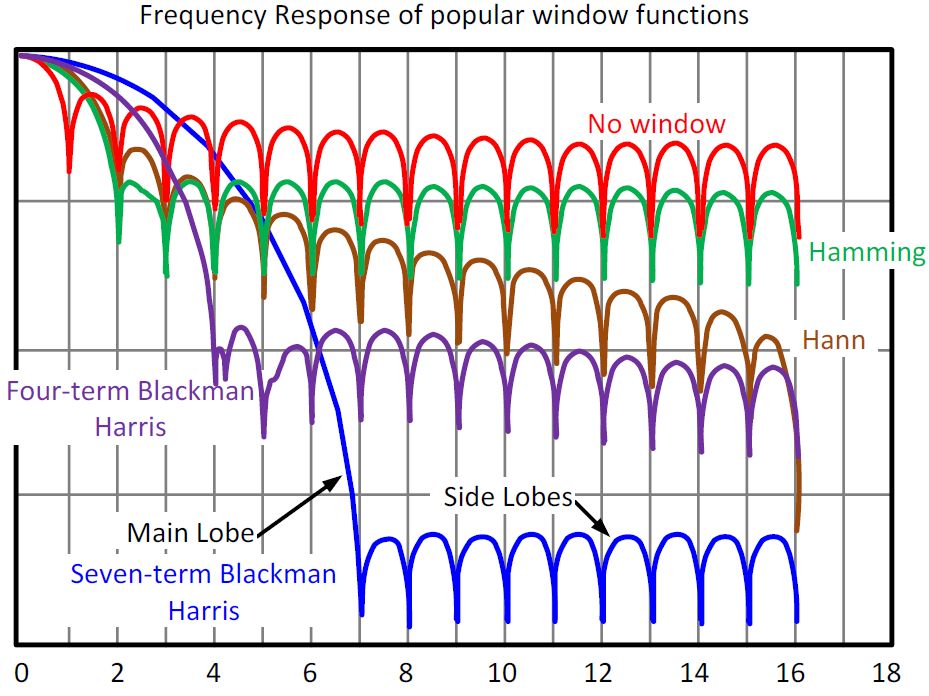
图：不同窗函数的频率响应比较

选择合适的窗函数可有效抑制泄漏，但需权衡频率分辨率、幅度精度和泄漏抑制效果（仅供参考）：

窗函数	适用信号类型	频率分辨率	频谱泄漏抑制	幅度精度
巴特利特窗	随机信号	良好	一般	一般
布莱克曼窗	随机或混合信号	较差	最佳	良好
平顶窗	正弦信号	较差	良好	最佳
汉宁窗	随机信号	良好	良好	一般
凯泽贝塞尔窗	随机信号	一般	良好	良好
无窗（矩形窗）	瞬态信号 & 同步采样	最佳	较差	较差

04

立思方RTSA

立思方推出了SURF系列产品，搭配立思方自研的荟谱实时频谱分析软件，针对复杂信号场景，集成多种窗函数，可根据信号类型自动匹配最佳窗：

获取完整产品资料或预约演示，可扫描下方二维码直达产品专员⬇⬇⬇