nowcoder刷题错题总结（6）

最新推荐文章于 2024-10-20 21:52:55 发布

inferno devil

最新推荐文章于 2024-10-20 21:52:55 发布

阅读量3.2k

点赞数 1

CC 4.0 BY-SA版权

分类专栏： nowcoder刷题

本文链接：https://blog.youkuaiyun.com/inferno_devil/article/details/91904824

nowcoder刷题专栏收录该内容

8 篇文章

订阅专栏

这篇博客总结了nowcoder上的数道经典数据结构与算法题目，涉及矩阵存储、循环队列、线性结构、二维数组访问、快速排序等概念。通过详细解析，帮助读者理解并掌握相关知识。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

01.设有一个10阶的对称矩阵A，采用压缩存储方式，以行序为主存储，a11为第一元素，其存储地址为1，每个元素占一个地址空间，则a85的地址为( )。
在这里插入图片描述解析:

由于是对称矩阵，因此压缩存储可以认为只要存储下三角矩阵。
(1,1)                                        1
(2,1) (2,2)                                  2
(3,1) (3,2) (3,3)                            3
(4,1) (4,2) (4,3) (4,4)                      4
(5,1) (5,2) (5,3) (5,4) (5,5)                5 
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)          6
(7,1) (7,2) (7,3) (7,4) (7,5) (7,6) (7,7)    7 
(8,1) (8,2) (8,3) (8,4) (8,5)                5
1+2+3+4+5+6+7+5=33
答案选B

对称矩阵的压缩矩阵表达式为：k=(i*(i-1)/2)+j。代入即可。

02.一个5*4的矩阵，有多少个长方形？（正方形也算是长方形）
在这里插入图片描述
解析：

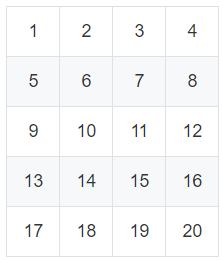
就像上面的表格，每一个格子可以说成是一个长方形，算的时候就是求这些边的组合：
竖着取两条边，C(6,2)。横着取两条边C(5,2)
所以结果就是：C(6,2)*C(5,2)=15*10=150

03.若用一个大小为 6 的数组来实现循环队列，且当 rear 和 front 的值分别为 0 和 3 。当从队列中删除一个元素，再加入两个元素后， rear 和 front 的值分别为。

解析：
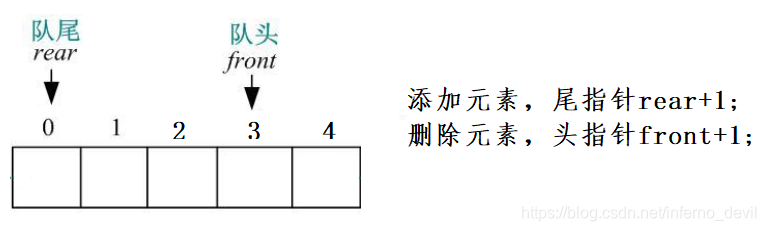
在这里插入图片描述

1、队列添加元素是在对尾，删除元素是在对头；
2、添加元素，尾指针rear+1;删除元素，头指针front+1;
3、本题中，删除一个元素，front+1,也就是3+1=4；添加2个元素，rear+2,也就是0+2=2；
4、选 B’

04.线性结构的是（）
在这里插入图片描述
解析：

串即为字符串，是一种特殊的线性表。串(String)是由零个或多个字符组成的有限序列，又称字符串。

 线性是线性，顺序是顺序，线性是逻辑结构，顺序是存储结构，两者不是一个概念。
 线性是指一个元素后继只有唯一的一个元素或节点，非线性是一个元素后面可以有多个后继或前继节点。
 顺序是指存储结构连续，例如数组是顺序的，链表不是顺序的，但他们都是线性的。当然顺序也可以是非线性的，例如顺序结构存储非线性结构的二叉树！！！

常用的线性结构有：线性表，堆栈，队列，双队列，数组，串。
常见的非线性结构有：二维数组，多维数组，广义表，树(二叉树等)，图。

05.以下是一个二维数组求和函数：

{
    int i, j, sum=0;
    for ( i=0; i< M; i++)
        for (j=0; j < N; j++)
            sum + =V[i] [j];
    return sum;
}

假设M=2、N=3，则数组V的访问顺序是( )时, 其访问局部性达到最好。（说明：二维数组存放时，一般同一行元素连续存放。）
在这里插入图片描述
解析：

 因为数组是顺序存储的，同一行的连续存放，A中首先是遍历第0行，然后是第1行，跳跃
只有1次。内存访问都在附近，叫程序的局部性。

06.设一组初始关键字记录关键字为(20，15，14，18，21，36，40，10)，则以20为基准记录的一趟快速排序结束后的结果为( )。
在这里插入图片描述
解析：

快速排序的算法是：

1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；
2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；
3）从j开始向前搜索，即由后开始向前搜索(j--)，找到第一个小于key的值A[j]，将A[j]和A[i]互换；
4）从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]互换；
5）重复第3、4步，直到i=j；

07.稀疏矩阵压缩存储后,必会失去随机存取功能()
在这里插入图片描述
解析：

 稀疏矩阵在采用压缩存储后将会失去随机存储的功能。因为在这种矩阵中，非零元素的分
布是没有规律的，为了压缩存储，就将每一个非零元素的值和它所在的行、列号做为一个
结点存放在一起，这样的结点组成的线性表中叫三元组表，它已不是简单的向量，所以无
法用下标直接存取矩阵中的元素。

 三元组表示法就是在存储非零元的同时，存储该元素所对应的行下标和列下标。稀疏矩阵
中的每一个非零元素由一个三元组(i,j,aij)唯一确定。矩阵中所有非零元素存放在由三元组组成的数组中。

在这里插入图片描述
08.设有一个n阶的下三角矩阵A，如果按照行的顺序将下三角矩阵中的元素（包括对角线上元素）存放在n(n+1)个连续的存储单元中，则A[i][j]与 A[0][0]之间有[ $KaTeX parse error: Expected 'EOF', got '#' at position 1: #̲#$ ]个数据元素（即不算A[i][j]和A[0][0]）。
在这里插入图片描述
解析：

09.一个非空广义表的表尾()
在这里插入图片描述
解析：

非空广义表的表头可以是原子或子表，表尾一定是子表。

10.数组A[0…4,-1…-3,5…7]中含有元素的个数()
在这里插入图片描述
解析：

三维数组：
长的边 个数 ：4-0+1=5
宽的边 个数 ：（-1）-（-3）+1=3
高的边 个数 ：7-5+1=3
总个数：5*3*3