Day 2 (前缀和 差分 二分 快速幂 逆元）

原创 已于 2025-01-16 15:21:02 修改 · 805 阅读 · 5 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #学习方法 #笔记 #c++ #数据结构

于 2025-01-15 22:02:54 首次发布

一.前缀和（一维，二维，三维）

模板

/*
一维前缀和
s[i] = s[i-1] + a[i];
查询 l - r 的和
s[r] - s[l-1] 
*/
/*
二维前缀和
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
查询 (x1,y1) - （x2,y2) 的和
s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]
*/

/*
三维前缀和
s[i][j][k] = s[i-1][j][k] + s[i][j-1][k] + s[i][j][k-1]
           - s[i-1][j-1][k] - s[i-1][j][k-1] - s[i][j-1][k-1]
           + s[i-1][j-1][k-1] + a[i][j][k];

查询（x1,y1,z1) - (x2,y2,z2) 的和
s[x2][y2][z2] - s[x1-1][y1-1][z1-1] - s[x1-1][y2][z2] - s[x2][y1-1][z2] - s[x2][y2][z1-1] 
              + s[x1-1][y1-1][z2] + s[x1-1][y2][z1-1] + s[x2][y1-1][z1-1];
*/

例题

Kobolds and Catacombs

思路：能够分开的点 前面的所有数一定小于后面所有数 可以利用前缀和来判断 s表示原数组的前缀和 presum 表示 排成升序的前缀和 当s[i] == presum[i] 时 ans++

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;
const int N = 1000010;
LL a[N];
LL presum[N];
LL s[N];
int ans;

int main()
{
    int n;
    cin >> n;
    for(int i = 1;i <= n;i++)
    {
        cin >> a[i];
        s[i] += s[i-1] + (LL)a[i];
    }
    sort(a + 1,a + n + 1);
    for(int i = 1;i <= n;i++) presum[i] += presum[i-1] + (LL)a[i];
    bool flag = true;
    for(int i = 1;i <= n;i++)
    {
        if(s[i] == presum[i]) ans++;
        else flag = false;
    }
    
    cout << ans << endl;
}

Cuboid Sum Query（三维前缀和 模板）

#include<bits/stdc++.h>
using namespace std;

const int N = 110;
typedef long long LL;
int a[N][N][N];
LL s[N][N][N];

int main()
{
    int n;
    cin >> n;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= n;j++)
            for(int k = 1;k <= n;k++)
                cin >> a[i][j][k];

    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= n;j++)
            for(int k = 1;k <= n;k++)
                s[i][j][k] = s[i-1][j][k] + s[i][j-1][k] + s[i][j][k-1] 
                - s[i-1][j-1][k] - s[i-1][j][k-1] - s[i][j-1][k-1] 
                + s[i-1][j-1][k-1] + (LL)a[i][j][k];
                
        
    int Q;
    cin >> Q;
    while(Q--)
    {
        int x1,x2,y1,y2,z1,z2;
        cin >> x1 >> x2 >> y1 >> y2 >> z1 >> z2;
        LL sum = s[x2][y2][z2] - s[x1-1][y1-1][z1-1] 
        - s[x1-1][y2][z2] - s[x2][y1-1][z2] - s[x2][y2][z1-1] 
        + s[x1-1][y1-1][z2] + s[x1-1][y2][z1-1] + s[x2][y1-1][z1-1] ;
        cout << sum << endl;
    } 
}

二.二分(二分查找，二分答案)

模板

/*
二分模板一

int l = 1,r = le9;
while(l <= r)
{
    int mid = l + r >> 1;
    if(check(mid)) r = mid;
    else l = mid + 1;
}
return r;
*/

/*
二分模板二

int l = 1,r = le9;
while(l <= r)
{
    int mid = l + r + 1 >> 1;
    if(check(mid)) l = mid;
    else r = mid - 1;
}
return l;
*/

例题

MaratonIME gets candies（交互题 猜数字）

#include<bits/stdc++.h>

using namespace std;

char ask(int x)
{
    cout << "Q" << " " << x << endl;
    char res;
    cin >> res;
    return res;
}

int main()
{
    int l = 1,r = 1e9;
    while(l <= r)
    {
        int mid = l + r >> 1;
        char op = ask(mid);
        if(op == '=') break;
        else if( op == '<') r = mid - 1;
        else l = mid + 1;
    }
}

Counting Pairs(二分边界范围)

 

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const LL N = 200010;
 
LL a[N];
LL n;
LL findl(LL x)//找到大于等于x的最左边的数的下标
{
    LL l = 0,r = n-1;
    while(l < r)
    {
        LL mid = l + r >> 1;
        if(a[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r;
}
 
LL findr(LL x)//找到小于等于x的最右边的数的下标
{
    LL l = 0,r = n - 1;
    while(l < r)
    {
        LL mid = l + r + 1>> 1;
        if(a[mid] <= x) l = mid;
        else r = mid - 1;
    }
    return l;
}
 
void solve()
{
    memset(a,0,sizeof a);//每次初始化一下a数组
    LL x,y;
    cin >> n >> x >> y;
    LL sum = 0;
    for(LL i = 0;i < n;i++)
    {
        cin >> a[i];
        sum += a[i];//求一下总和
    }
    /*
        要求的是 x <= sum - a[i] - a[j] <= y
        那么我们可以枚举每一个a[i] 那么对应的a[j] 就有范围
        sum - a[i] - y <= a[j] <= sum - a[i] - x
        因为我们对元素组排序 所以可以二分数俩个端点
    */
 
 
    sort(a,a+n);//可以发现选的数其实跟位置没关系 因为俩个数 总是前后关系
    LL ans = 0;
    for(LL i = 0;i < n;i++)
    {
        LL res = 0;
        LL left = sum - (LL)a[i] - y;//求出左端点大小
        LL right = sum - (LL)a[i] - x;//求出右端点大小
        LL l = findl(left);//找一下大于等于左端点的最右端的位置
        if(a[l] < left) continue;//如果左端点（也就是a[l] 已经为 数组当中最大值）找不到 跳过
        LL r = findr(right);
 
        if(r <= i) break;//如果右端点下标是小于i的 那么不用再找了 因为右端点值只会越来越小
                        //后面的条件越苛刻 当前条件都满足不了 就不用再继续了
 
        if(l <= i) l = i + 1;//我们只计算在i右边的区间 这样避免了重复计算
        res = r - l + 1;
        ans += res;//累加一下答案
    }
    
    cout << ans << endl;
}
 
int main()
{
    LL T;
    cin >> T;
    while(T--)
    {
        solve();
    }
    return 0;
}

 Largest Allowed Area（二分答案 + 二维前缀和）

#include<bits/stdc++.h>
using namespace std;

const int N = 2020;
int g[N][N];
int s[N][N];
int n,m;
// 不使用快读会TLE
#define Temp template<typename T>
Temp inline void read(T &x)
{
    x=0;T w=1,ch=getchar();
    while(!std::isdigit(ch)&&ch!='-')ch=getchar();
    if(ch=='-')w=-1,ch=getchar();
    while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
    x=x*w;
}

bool check(int x)
{
    //枚举左上横坐标 对应得到右下横坐标
    for(int x1 = 1;x1 + x - 1 <= n;x1 ++)
    {
        int x2 = x1 + x - 1;
        //枚举左上纵坐标 对应得到右下纵坐标
        for(int y1 = 1;y1 + x - 1 <= m ;y1 ++)
        {
            int y2 = y1 + x - 1;
            int cnt = s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1 - 1][y1 - 1];
            if(cnt <= 1) return true;
        }
    }
    return false;
}

void solve()
{
    cin >> n >> m;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
        {
            read(g[i][j]);
        }

    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + g[i][j];

    int l = 1,r = min(n,m);//边长最长为min(n,m);
    int ans = 1;
    while(l <= r)
    {
        int mid = l + r >> 1;
        if(check(mid))
        {
            ans = mid;
            l = mid + 1;
        }
        else r = mid - 1;
    }
    cout << ans << endl;

    
}

int main()
{
    int T;
    read(T);
    while(T--)
    {
        memset(g,0,sizeof g);
        memset(s,0,sizeof s);
        solve();
    }
    return 0;
}

Max Median（二分答案）

#include<bits/stdc++.h>
using namespace std;

const int N = 200010;
int a[N],tmp[N];
int n,k;
int cnt[N];


bool check(int mid)
{
    for(int i = 1;i <= n;i++)
    {
        if(a[i] >= mid) cnt[i] = 1;
        else cnt[i] = -1;
    }

    for(int i = 1;i <= n;i++) cnt[i] += cnt[i-1];
    int minv = 0;
    for(int i = k;i <= n;i++)
    {
        if(cnt[i] - minv > 0) return true;
        minv = min(cnt[i - k + 1],minv);
    }
    return false;
}


int main()
{
    cin >> n >> k;
    for(int i = 1;i <= n;i++)
        cin >> a[i],tmp[i] = a[i];
    //将元素组升序排序 二分最大中位数
    sort(tmp + 1,tmp + n + 1);

    int l = 1,r = n;
    while(l < r)
    {
        int mid = l + r + 1 >> 1;
        if(check(tmp[mid])) l = mid;
        else r = mid - 1;
    }
    cout << tmp[l] << endl;
    return 0;
}

三.快速读写

模板

#include<bits/stdc++.h>
#define Temp template<typename T>
//避免为不同的数据类型重复编写相同逻辑的函数或类
using namespace std;
//这样，对于任何类型 T，只要支持拷贝构造和赋值操作，该函数都可以使用，无需为每种类型单独编写函数。
Temp inline int read(T & x)
{
    x = 0;
    T w = 1,ch = getchar();
    while(ch <= '0' && ch >= '9')
    {
        if(ch == '-') w *= -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
    x = x * w;
}

四.差分

例题

 Karen and Coffee

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 200010;
int d[N];
int cnt[N];
int n,q,k;
int main()
{
    cin >> n >> k >> q;
    for(int i = 0;i < n;i++)
    {
        int l,r;
        cin >> l >> r;
        d[l] ++;
        d[r+1] --;
    }
    for(int i = 1;i <= N;i++) d[i] += d[i-1];
    for(int i = 1;i <= N;i++)
    {
        if(d[i] >= k) cnt[i] = 1;
        cnt[i] += cnt[i-1];
    }
    while(q--)
    {
        int l,r;
        cin >> l >> r;
        cout << cnt[r] - cnt[l-1] << endl;
    }
}

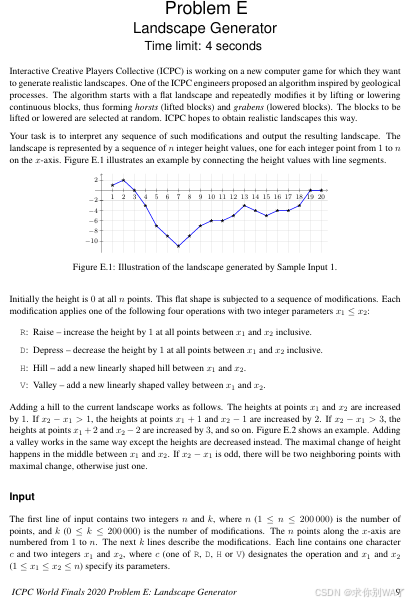
Landscape Generator

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200010;
LL d[N];//对于前俩个操作 的差分数组
LL tmpd[N];//对于后俩个操作的差分数组 （二次差分）
int n,k;

int main()
{
    cin >> n >> k;
    while(k--)
    {
        char op;
        int l,r;
        cin >> op >> l >> r;
        if(op == 'R') d[l] ++,d[r + 1] --;
        else if(op == 'D') d[l] --,d[r + 1] ++;
        else if(op == 'H')
        {
            int mid = l + r >> 1;
            int len = r - l + 1;
            if(len % 2 == 0)//分奇偶讨论
            {
                tmpd[l] ++,tmpd[mid + 1] --;
                tmpd[mid + 2] --,tmpd[r + 2] ++;
            }
            else
            {
                tmpd[l] ++,tmpd[mid + 1] -= 2;
                tmpd[r + 2] ++;
            }
        }
        else if(op == 'V')
        {
            int mid = l + r >> 1;
            int len = r - l + 1;
            if(len % 2 == 0)
            {
                tmpd[l] --,tmpd[mid + 1] ++;
                tmpd[mid + 2] ++,tmpd[r + 2] --;
            }
            else
            {
                tmpd[l] --,tmpd[mid + 1] += 2;
                tmpd[r + 2] --;
            }
        }
    }
    for(int i = 1;i <= n;i++)
    {
        tmpd[i] += tmpd[i-1];
        d[i] += d[i-1] + tmpd[i];
    }

    for(int i = 1;i <= n;i++) cout << d[i] << endl;

}

五.快速幂（模板以及求逆元）

模板

LL qmi(LL a,LL k,LL p)
{
    LL res = 1;
    while(k)
    {
        if(k & 1) res = res * a % p;
        k >>= 1;
        a = a * a % mod;
    }
    retrun res;
}

//求逆元
LL vni(LL x)
{
    return qmi(x,p-2);
}

例题

Plant（快速幂+数学推导）

up为an down 为bn

可以发现 an - bn = 2^(n-1)

an + bn = 4^(n-1)

可以求出an 注意题目的第一项跟这里第一项不太一样

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
typedef long long LL;

const int mod =  1000000007;
LL qmi(LL a,LL k)
{
    a %= mod;
    LL res = 1;
    while(k)
    {
        if(k & 1)
        {
            res = (res * a) % mod;
        }
        k >>= 1;
        a = (a * a) % mod;
    }
    return res;
}
LL up,down;
int main()
{
    LL n;
    cin >> n;
    if(n == 0) puts("1");
    else cout << (qmi(2,n * 2 - 1) + qmi(2,n-1)) % mod << endl;
    
}

Hamsters Training(逆元求组合数)

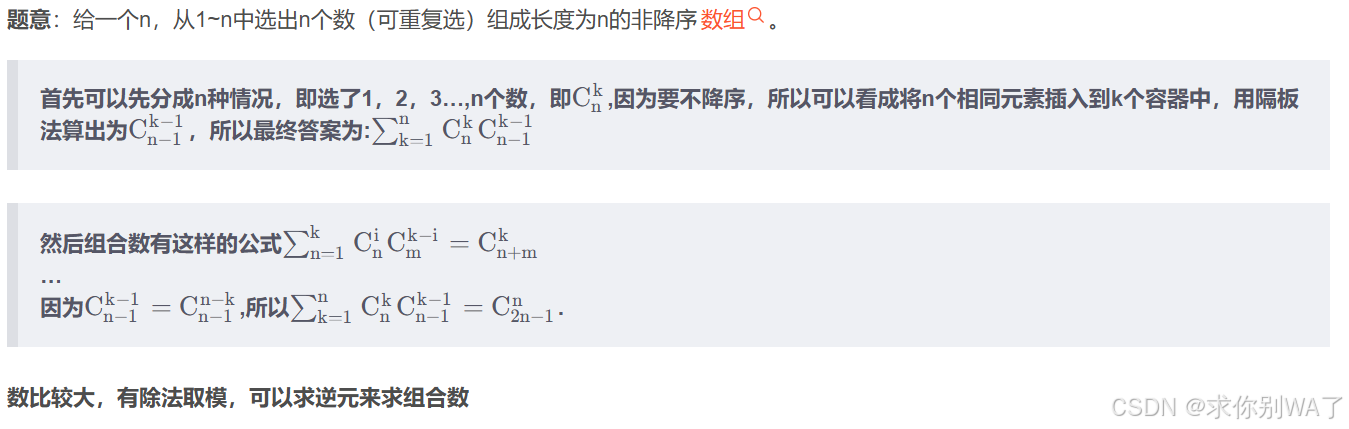
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1e9+7;

LL fa[N],fb[N];

LL qmi(LL a,LL b)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}

LL C(LL n,LL k)
{
    return fa[n] * fb[k] % mod * fb[n - k] % mod;
}

void init()
{
    fa[0] = fb[0] = 1;
    for(int i = 1;i < N;i++)
    {
        fa[i] = fa[i-1] * i % mod;
        fb[i] = qmi(fa[i],mod - 2) % mod;
    }
}

void solve()
{
    int n;
    cin >> n;
    cout << C(2 * n - 1,n)   << endl;
}

int main()
{
    init();
    int T;
    cin >> T;
    while(T--)
    {
        solve();
    }
}

夜深人静写算法（三十）- 二分快速幂
英雄哪里出来
02-08 6888
开启数论的征程
7月清北学堂培训 Day 2
weixin_30595035的博客
07-14 271
今天是林永迪老师的讲授~ 继续昨日的贪心内容。 我们继续看例题： 分析样例的过河方法： 首先1和2先过河，总时间为2； 然后1回来，总时间为3； 然后5和10过河，总时间为13； 然后2回来，总时间为15； 然后1和2过河，总时间为17； 一个很强烈的贪心思路：最慢和次慢的两个人一定要一起过河； 证明： 假设我们有四个人 A B C D，他们过河时间是依次增大的。 ...
矩阵快速幂 快速求解递推公式
牛牛博士博客
05-05 1026
矩阵快速幂 快速求解递推公式
22牛客多校day9 B - Chiitoitsu 概论dp 线性逆元 + 差分优化
Szyang
08-15 250
22牛客多校day9 B - Chiitoitsu 概论dp 线性逆元 + 差分优化
Python·算法分类题库
欢迎关注Blog：https://www.cnblogs.com/Chiaki17/category/2410756.html
08-06 1556
欢迎关注【Python·算法分类题库】，持续更新中……
noip2011 day2
Bluelanzhan的博客
04-14 320
1．计算系数 (factor.cpp/c/pas) 【问题描述】 给定一个多项式(ax + by)k，请求出多项式展开后xn ym项的系数。 【输入】 输入文件名为 factor.in。 共一行，包含 5 个整数，分别为a，b，k，n，m，每两个整数之间用一个空格隔开。 【输出】 输出文件名为 factor.out。 输出共 1 行，包含一个整数，表示所求的系数，这个系数可能很大，输出对10007...
NOIP2011提高组day2
weixin_30408309的博客
04-18 139
NOIP 2011 提高组 Day 2 T1 ： 题意： 这道题题意很显然，方法就是利用数学中的二项式定理 ： ( x + y ) ^ n = C ( i , n ) * x ^ i * y ^ ( n - i )，i ∈ [ 0 , n ]，所以求x ^ n * y ^ m的系数，就是求C( n , k ) * a ^ n * b ^ m再模上10007，注意求C( n ...
2019 CCPC-Wannafly Winter Camp Day3(Div2, onsite)
weixin_30631587的博客
01-22 143
solve 4/11 补题：5/11 A二十四点* Code：pai爷 zz Thinking ：pai爷 打表找规律，1张牌 10个不可能的 2张牌有 43 种不可能的 3张牌 有74 种不可能的 4 张牌有 5 种不可能的 #include<iostream> #include<cstring> #include<cmath&...
【刷题计划1】【poj分类转载】
loving coding
08-19 1387
----------------2018.4.10更新-----------------------原本这只是暑假刷题计划，后来因为某些原因，自己就不是很努力的刷题，现在情况有变，so，重新继续咯~下个月26号省赛，扣去中间实训的一周时间和几次校赛，大概只有一个月时间。目前计划是，每天基础算法题+cf上3题，专业课也先停了，自己这段时间只想认真写题。昨天晚上又失眠了，虽然我知道保证训练效率的关键是...
快速幂+逆元求组合数
mathematicians的博客
12-08 498
快速幂是一种高效计算的方法。它利用指数的二进制表示，巧妙地减少了乘法次数，把原本复杂的幂运算大幅加速。通过快速幂的指数分解和模逆元的逆运算，我们轻松解决了组合数计算中的「模运算」难题。无论是科普练习还是竞赛题目，这套方法都是高效又实用的工具！快来试试，解锁你的数学超能力吧！🎉a%5Eb。
精选资源
组合计数 （四）1.递归 2. 快速幂求逆元 3.卢卡斯定理 4.阶乘分解加大数据乘法运算
01-03
a,b较小时 2000 #include using namespace std; const int N = 2010, mod = 1e9 + 7; int c[N][N]; int n; int main() { cin >> n;...a,b较大时 利用乘法逆元求 a,b为10^5 #include #include #inclu
快速幂求逆元-C语言
AlanKSorata的博客
03-15 950
记下求逆元的方法，以后补上别的语言
欧几里得距离算法-相似度
weixin_45609702的博客
12-04 196
本文介绍了一个计算欧几里得距离的Java方法。该方法接收两个Double数组作为输入，通过计算对应元素差值的平方和再开方，返回两个数组之间的欧几里得距离值。当输入数组长度不一致时，方法会返回0作为默认值。欧几里得距离算法常用于比较两个数组之间的相似度，是数据分析和机器学习中的基础距离度量方法。
练题100天——DAY21：统计奇数个数+合并有序数组
最新发布
2301_81099859的博客
12-07 252
今天写了两道题，难度，并更新了之前的DAY13的冒泡排序+二进制求和、DAY14全排列的思路。
Leetcode 68 搜索插入位置 | 寻找比目标字母大的最小字母
im_AMBER的博客
12-04 1036
你的错误逻辑正确逻辑找到 target 时返回 mid-1找到 target 时，继续向右查找（因为需要「大于」target 的最小字符）target <letters [mid] 时，mid 是候选，需保留，right=mid（左闭右开）或不立即排除 mid循环结束直接返回 letters [0]循环结束后，先判断 left 是否越界：越界则返回 letters [0]，否则返回 letters [left]初始right的取值与「越界判断」不匹配；
C++ ⼀级 2024 年 03 ⽉
weixin_46669997的博客
12-05 35
当 N 为9, 6, 3, 0时，满足条件 N % 3 == 0，因此它们被输出并跟随一个 #。要注意的是，字符串“a+1= ”最后有一个空格，因而输出的内容是：a+1= 2，答案为A。输入21，21%3的结果为0，进入if的分支，因而第4行代码可以被执行。19.【判断题】C++表达式 “10”*2 执行时将报错，因为 “10” 是字符串类型而2是整数类型，它们数据类型不同，不能在一起运算。Cout后面有两个<<，第1个输出字符串5%2=，第2个输出算术运算“5%2”的结果，为1，答案为D。
浅谈：快递物流与算法的相关性（五）
Duoya1105的博客
12-05 164
NP-C 的英文全称是 Non-deterministic Polynomial Complete，即多项式复杂程度的非确定性问题。简单的写法是NP=P？，问题就在这个问号上，到底有没有让NP=P的算法，或是如何证明NP≠P。启发式算法的思想是：在不断解决问题的过程中寻找解决问题的最优方案。再举一个通俗的例子：当我们用数字密码解锁手机时，如果我们不知道密码是多少，必须将所有的数字组合依次尝试。这听起来像是一句废话，如果将它抽象一点的表述，就是：能用电脑快速验证一个解的问题，是否也能够用电脑快速地求出解。
[优选算法专题十.哈希表 ——NO.55~57 两数之和、判定是否互为字符重排、存在重复元素]
2401_83386596的博客
12-03 689
两数之和问题的最优解法采用哈希表实现O(n)时间复杂度，通过存储元素值与下标的映射关系，快速查找互补值。字符重排判定问题通过单哈希数组统计字符出现次数，先加后减并实时校验，确保字符种类和数量完全一致。存在重复元素问题使用哈希集合检测重复元素，遍历数组时检查元素是否已存在于集合中。三种解法均利用哈希结构优化查找效率，将时间复杂度从暴力解法的O(n²)降至O(n)，是典型空间换时间策略的工业级实现。
简单多源BFS问题
MiauwYuki的博客
12-03 192
简单多源BFS问题
C语言快速幂和快速幂求逆元
11-21
以下是C语言实现快速幂和快速幂求逆元的代码： 1. 快速幂 ```c #include typedef long long LL; // a^k % p int qmi(int a, int k, int p) { int res = 1; while (k) { if (k & 1) res = (LL)res * a % p; ...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值