1 单选题（每题 2 分，共 30 分）
第1题 下列哪一项不是面向对象编程（OOP）的基本特征？（ ）
A. 继承 (Inheritance) B. 封装 (Encapsulation)
C. 多态 (Polymorphism) D. 链接 (Linking)
解析：答案D。面向对象编程的基本特征包含封装、继承、多态和抽象四大核心要素，这四大特征共同构成了代码组织的核心范式，有效提升了程序的可维护性、扩展性和复用性。所以D.不是。故选D。
第2题 为了让 Dog 类的构造函数能正确地调用其父类 Animal 的构造方法，横线线处应填入（ ）。
- class Animal:
- def __init__(self, name: str):
- self.name = name
- print("Animal created")
- def speak(self) -> None:
- print("Animal speaks")
- class Dog(Animal):
- ______________________________
- print("Dog created")
- def speak(self) -> None:
- print("Dog barks")
- if __name__ == "__main__":
- animal: Animal = Dog("Rex", "Labrador")
- animal.speak()
|
A. |
|
|
B. |
|
|
C. |
|
|
D. |
|
解析：答案A。继承父类构造函数：子类 Dog 需要通过 super().__init__(name) 显式调用父类 Animal 的构造函数，以确保执行父类构造函数（如 self.name = name 和打印 "Animal created"）被执行。扩展子类属性：Dog 类新增了 breed 属性，需要在子类构造函数中初始化 self.breed = breed。所以A.的代码完全符合上述逻辑，而其他选项（B.、C.、D.）要么遗漏了 super().__init__()，要么语法不完整。故选A。
第3题 代码同上一题，代码animal.speak()执行后输出结果是（ ）。
A. 输出 Animal speaks B. 输出 Dog barks C. 编译错误 D. 程序崩溃
解析：答案B。Dog 实例化时，通过 super().__init__("Rex") 调用父类 Animal 的构造函数，执行 print("Animal created") 并初始化 name 属性。Dog 的构造函数继续执行 print("Dog created")。最后调用 animal.speak()，由于 Dog 重写了 speak 方法，输出 "Dog barks"，所以输出 Dog barks。故选B。
第4题 以下Python代码执行后其输出是（ ）。
- from collections import deque
- stack = []
- queue = deque()
- # 元素入栈/入队（1, 2, 3）
- for i in range(1, 4):
- stack.append(i)
- queue.append(i)
- print(f"{stack[-1]} {queue[0]}")
A. 1 3 B. 3 1 C. 3 3 D. 1 1
解析：答案B。栈和队列的操作：栈（stack）是先进后出（FILO）结构，本题用列表模拟，append(i) 依次添加 1, 2, 3，因此 stack[-1]（栈顶元素，列表最后的元素）为 3。队列（deque）是先进先出（FIFO）结构， append(i) 依次添加 1, 2, 3，因此 queue[0]（队首元素）为 1。所以输出结果为f"{stack[-1]} {queue[0]}"的结果为 "3 1"。故选B。
第5题 在一个使用列表实现的循环队列中，front 表示队头元素的位置（索引），rear 表示队尾元素的下一个插入位置（索引），队列的最大容量为 maxSize。那么判断队列已满的条件是（ ）
A. rear == front B. (rear + 1) % maxSize == front
C. (rear - 1 + maxSize) % maxSize == front D. (rear - 1) == front
解析：答案B。在循环队列中，判断队列已满的条件需要满足以下两点：队尾指针（rear）的下一个位置是队头指针（front），即 rear 即将追上 front。为了避免rear == front时出现歧义（此时队列可能为空也可能为满），通常使用 (rear + 1) % maxSize == front 来判断是否已满。rear == front用于判断空队列，所以A.错误。(rear - 1 + maxSize) % maxSize == front：
等价于 rear - 1 == front，C.、D.相同，所以两者都错。故选B。
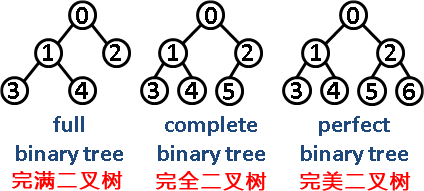
第6题 在二叉树中，只有最底层的节点未被填满，且最底层节点尽量靠左填充的是（ ）。
A. 完美二叉树 B. 完全二叉树 C. 完满二叉树 D. 平衡二叉树
解析：答案B。完美二叉树(Perfect Binary Tree)：一个深度为k(>=1)且有2^(k-1) - 1个结点的二叉树称为完美二叉树。(注：国内的数据结构教材大多翻译为"满二叉树")。完全二叉树(Complete Binary Tree)：完全二叉树从根结点到倒数第二层满足完美二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐。完满二叉树(Full Binary Tree)：所有非叶子结点的度都是2。（只要你有孩子，你就必然是有两个孩子。）所以B.正确。故选B。
第7题 在使用数组(列表)表示完全二叉树时，如果一个节点的索引为𝑖（从0开始计数），那么其左子节点的索引通常是（ ）。
A.(i-1)/2 B.i+1 C.i+2 D.2*i+1
解析：答案D。在使用数组表示完全二叉树时，节点的索引从0开始，其子节点的索引计算规则为：左子节点的索引为2*i + 1，右子节点的索引为2*i + 2。例如：根节点 i = 2：左子节点 i = 2*2 + 1 = 5，右子节点 i = 2*2 + 2 = 6，D.正确。故选D。
第8题 已知一棵二叉树的前序遍历序列为GDAFEMHZ，中序遍历序列为ADFGEHMZ，则其后序遍历序列为（ ）。
A. ADFGEHMZ B. ADFGHMEZ C. AFDGEMZH D. AFDHZMEG
解析：答案D。由前序遍历序列可知根节点为G，由中序遍历序列可知左树为AFD，右树为EHMZ，后序遍历序列左树、右树、根节点，只有D.的结构符合。具体：前序遍历（根-左-右）的第一个元素 G 是根节点。中序遍历（左-根-右）中，G 左侧 ADF 是左子树，右侧 EMHZ 是右子树。前序遍历左子树 DAF ，中序遍历左树 ADF，D子树根，左节点A，右节点F。前序遍历右子树EMHZ，中序遍历右子树EHMZ，E为子树根，只有右子树。前序遍历E右子树MHZ，中序遍历E右子树HMZ，M为子树根，左节点为H，右节点为Z。构成二叉树为：
所以后序遍历序列为AFDHZMEG，D.正确。故选D。
第9题 设有字符集 {a, b, c, d, e}，其出现频率分别为 {5, 8, 12, 15, 20}，得到的哈夫曼编码为（ ）。
|
A. |
|
B. |
|
C. |
|
D. |
|
解析：答案A。哈夫曼编码的特点，频率低的用长编码，频率高的用短编码。a最低，b次之，d次高，e最高，e短编码、a长编码，d短编码，b长编码，只有A.符合。具体：a合并b为13，c合并13(ab)为25，d合并e为35，25合并35为60。
A.正确。故选A。
第10题 3位格雷编码中，编码101之后的下一个编码是（ ）。
A. 100 B. 111 C. 110 D. 001
解析：答案C。格力雷编码中，相邻两处码只有一位变化。编码 101 在标准序列中的下一个编码应为 100（仅最低位变化），次序与高位为0的次序相反，A.正确。111是110 的下一个编码，非 101 的相邻码。110 和 001 与 101 的汉明距离大于1，不符合格雷码规则。故选A。
第11题 请将下列Python实现的深度优先搜索（DFS）代码补充完整，横线处应填入（ ）。
- from typing import List, Optional
- class TreeNode:
- def __init__(self, val=0, left=None, right=None):
- self.val = val
- self.left = left
- self.right = right
- def dfs_preorder(root: Optional[TreeNode], result: List[int]) -> None:
- if root is None:
- return
- _____________________________
|
A. |
|
|
B. |
|
|
C. |
|
|
D. |
|
解析：答案A。题目要求补充一个深度优先搜索（DFS）的代码片段，二叉树的深度优先分为:先序遍历、中序遍历、后序遍历。观察选项可以发现，除D.外result.append()都在第1行，属前序遍历，属前序遍历顺序是：根节点 → 左子树 → 右子树，因此应 result.append(root.val)，再递归遍历左、右子树，所以A.正确。B.缺少右子树的遍历，C.缺少左子树的遍历，D.没有访问根节点，所以B.、C.、D.错误。故选A。
第 12 题 给定一个二叉树，返回每一层中最大的节点值，结果以数组形式返回，横线处应填入（ ）。
- from collections import deque
- import math
- from typing import List, Optional
- class TreeNode:
- def __init__(self, val=0, left=None, right=None):
- self.val = val
- self.left = left
- self.right = right
- def largestValues(root: Optional[TreeNode]) -> List[int]:
- result = []
- if not root:
- return result
- queue = deque([root])
- while queue:
- level_size = len(queue)
- max_val = -math.inf
- for _ in range(level_size):
- ________________________
- if node.left:
- queue.append(node.left)
- if node.right:
- queue.append(node.right)
- result.append(max_val)
- return result
|
A. |
|
B. |
|
|
C. |
|
D. |
|
解析：答案D。题目要求实现按层遍历二叉树并返回每层最大值，使用广度优先搜索（BFS），编程使用队列。使用队列 deque 逐层处理节点。每层开始时，用 level_size 记录当前层节点数，遍历当前层所有节点，记录最大值 max_val。queue.popleft() 是BFS的标准操作（先进先出），确保按层顺序处理节点，max_val = max(max_val, node.val) 动态更新当前层的最大值，所以D.正确。popright() 不是 deque 的有效方法，且逻辑错误，所以A.错误。B.缺少更新 max_val 的步骤，无法记录最大值、C.缺少 node = queue.popleft()，无法获取节点值进行比较，所以B.、C.错误。故选D。
第13题 下面代码实现一个二叉排序树的插入函数（没有相同的数值），横线处应填入（ ）。
- class TreeNode:
- def __init__(self, val=0, left=None, right=None):
- self.val = val
- self.left = left
- self.right = right
- def insert(root, key):
- if root is None:
- return TreeNode(key)
- ___________________________
- return root
|
A. |
|
|
B. |
|
|
C. |
|
|
D. |
|
解析：答案A。题目要求实现二叉排序树（BST）的插入操作，且不允许重复值。BST的插入规则是：(1)如果当前节点为null，创建新节点。(2)如果 key 小于当前节点值，递归插入左子树。(3)如果 key 大于当前节点值，递归插入右子树。因不允许重复值，所以相等不处理。A.正确实现BST插入逻辑（左小右大），所以正确。B.左小，但否则条件永不成立，所以错误。C. elif key >= root.val 会导致重复值（题目不允许）且全部插入到左子树，所以错误。D. 左右子树插入逻辑完全颠倒（左子树插入右子树，右子树插入左子树），所以错误。故选A。
第14题 以下关于动态规划算法特性的描述，正确的是（ ）。
A. 子问题相互独立，不重叠 B. 问题包含重叠子问题和最优子结构
C. 只能从底至顶迭代求解 D. 必须使用递归实现，不能使用迭代
解析：答案B。动态规划（Dynamic Programming, DP）的核心特性包括：1)重叠子问题：问题可以被分解为重复出现的子问题，通过记忆化或表存储避免重复计算；2)最优子结构：问题的最优解包含其子问题的最优解，从而能够递推求解。 B. 问题包含重叠子问题和最优子结构，正确。A.动态规划的子问题通常是重叠的（否则可直接用分治法解决），错误。C.动态规划可以从顶至底（递归+记忆化）或底至顶（迭代）两种方式求解，错误。D.动态规划的实现既支持递归，也支持迭代，错误。故选B。
第15题 给定𝑛个物品和一个最大承重为𝑊的背包，每个物品有一个重量𝑤𝑡[𝑖]和价值𝑣𝑎𝑙[𝑖]，每个物品只能选择放或不放。目标是选择若干个物品放入背包，使得总价值最大，且总重量不超过𝑊。关于下面代码，说法正确的是（ ）。
- def knapsack1D(W: int, wt: list[int], val: list[int], n: int) -> int:
- dp = [0] * (W + 1)
- for i in range(n):
- for w in range(W, wt[i] - 1, -1):
- dp[w] = max(dp[w], dp[w - wt[i]] + val[i])
- return dp[W]
A. 该算法不能处理背包容量为 0 的情况
B. 外层循环 i 遍历背包容量，内层遍历物品
C. 从大到小遍历 w 是为了避免重复使用同一物品
D. 这段代码计算的是最小重量而非最大价值
正确答案：C. 从大到小遍历 w 是为了避免重复使用同一物品
解析：答案C。本题代码实现的是0/1背包问题的经典动态规划解法，使用一维数组 dp[w] 表示容量为 w 时的最大价值。外层循环遍历物品（i），内层循环从大到小遍历背包容量（w），目的是确保每个物品仅被使用一次。当 W=0 时，dp[0] 初始化为 0，直接返回 0，能正确处理，所以A.错误。外层循环遍历物品（i），内层循环遍历背包容量（w），B.反了，所以错误。从大到小遍历 w 是为了避免覆盖 dp[w - wt[i]]，从而防止同一物品被重复使用，C.正确。代码明确计算的是最大价值（max(dp[w], dp[w - wt[i]] + val[i])），D.错误。故选C。
2 判断题（每题 2 分，共 20 分）
第1题 构造函数只能自动不可以被手动调用。（ ）
解析：答案错误。Python的构造函数（__init__）可以通过特定方式手动调用。故错误。
第2题 给定一组字符及其出现的频率，构造出的哈夫曼树是唯一的。（ ）
解析：答案错误。当存在多个相同权值的节点时，合并顺序不同会导致不同的树形结构。例如，频率集合{2,2,3,3}，因同频次序调整，可能生成多种不同形态的哈夫曼树，但他们的带权路径长度（WPL）是相同的。故错误。
第3题 为了实现一个队列，使其出队操作（ pop ）的时间复杂度为O(1)并且避免数组删除首元素的O(n)问题，一种常见且有效的方法是使用环形数组，通过调整队首和队尾指针来实现。（ ）
解析：答案正确。题目描述的实现队列的方式是环形数组（列表）组成循环队列，其核心思路确实是通过调整队首（front）和队尾（rear）指针来高效进行出入队操作，避免移动数组元素的开销。环形数组的：当队尾指针到达数组末尾时，可以绕回到数组开头（环形结构），避免频繁扩容或移动元素。入队（push）：rear = (rear + 1) % capacity（O(1)）；出队（pop）：front = (front + 1) % capacity（O(1)）。传统数组队列删除首元素需要移动后续所有元素（O(n)），而环形队列仅需移动指针（O(1)）。故正确。
第4题 对一棵从小到大的二叉排序树进行中序遍历，可以得到一个递增的有序序列。（ ）
解析：答案正确。二叉排序树的定义：
左子树的所有节点值 小于 当前节点值。右子树的所有节点值 大于 当前节点值。
中序遍历（左-根-右）的特性：先遍历左子树（所有值更小），再访问根节点，最后遍历右子树（所有值更大）。因此，中序遍历结果必然按升序排列。故正确。
第5题 如果二叉搜索树在连续的插入和删除操作后，所有节点都偏向一侧，导致其退化为类似于链表的结构，这时 其查找、插入、删除操作的时间复杂度会从理想情况下的O(log n)退化到O(n log n)。（ ）
解析：答案错误。二叉搜索树（BST）又称二叉查找树或二叉排序树。题目考察二叉搜索树（BST）退化后的时间复杂度，判断其查找、插入、删除操作是否会从 O(log n) 退化为 O(n log n)。理想情况（平衡BST）查找、插入、删除的时间复杂度为O(log n)。退化情况（退化为链表）：树高度变为n，操作需遍历所有节点，时间复杂度退化为 O(n)。
退化原因：若插入或删除的序列有序（如连续递增或递减），BST会退化为单侧链表，树高度从 log n 变为 n。如上图所示。查找：需遍历整条“链”，时间复杂度 O(n)。插入/删除：同样需遍历到末端或目标位置，时间复杂度O(n)，而不是O(n log n)，所以错误。
第6题 执行下列代码， my_dog.name 的最终值是 Charlie 。（ ）
- class Dog:
- def __init__(self, name):
- self.name = name
- if __name__ == "__main__":
- my_dog = Dog("Buddy")
- my_dog.name = "Charlie"
解析：答案正确。构造函数初始化（第2行）：def __init__(self, name):为传入的name字符串。第6行用Dog类建my_dog对象my_dog=Dog("Buddy") 会调用构造函数，将 name 初始化为 "Buddy"。第7行给对象成员赋值，修改成员变量，my_dog.name = "Charlie" 显式修改name的值为"Charlie"，my_dog.name 的最终值为 "Charlie"，所以正确。
第7题 下列 python 代码可以成功执行，并且子类 Child 的实例能通过其成员函数访问父类 Parent 的属性 _value 。（ ）
- class Parent:
- def __init__(self):
- self._value = 100
- class Child(Parent):
- def get_protected_val(self):
- return self._value
解析：答案：正确。Child 继承自 Parent，因此 Child 的实例会调用 Parent.__init__() 并初始化 self._value（值为100）。_value 是单下划线前缀的“受保护”属性（约定俗成，非语法强制），子类可通过 self._value 直接访问。get_protected_val() 方法返回 self._value，逻辑正确。故正确。
第8题 下列代码中的 tree 列表，表示的是一棵完全二叉树 ( -1 代表空节点)按照层序遍历的结果。（ ）
- tree = [1, 2, 3, 4, -1, 6, 7]
解析：答案错误。完全二叉树的定义：除最后一层外，其他层节点必须完全填充（无空缺）。最后一层节点从左到右连续排列（不能有中间空缺）。层序遍历结果：[1, 2, 3, 4, -1, 6, 7]（-1 表示空节点）。
第3层（节点索引4）：值为 -1（空节点，参考上图），但后续仍有 6 和 7 节点。违反完全二叉树“最后一层节点从左到右连续排列（不能有中间空缺）”的规则，该树不是完全二叉树，所以错误。
第9题 在树的深度优先搜索（DFS）中，可以使用栈作为辅助数据结构以实现“先进后出”的访问顺序。（ ）
解析：答案正确。树的深度优先搜索（DFS）确实使用栈作为辅助数据结构，其“先进后出”（FILO）特性确保优先深入探索分支，符合DFS的核心逻辑。故正确。
第10题 下面代码采用动态规划求解零钱兑换问题：给定 𝑛 种硬币，第 𝑖 种硬币的面值为 𝑐𝑜𝑖𝑛𝑠[𝑖 − 1] ，目标金额为 𝑎𝑚𝑡 ，每种硬币可以重复选取，求能够凑出目标金额的最少硬币数量；如果不能凑出目标金额，返回 -1 。（ ）
- def coinChangeDPComp(coins: list[int], amt: int) -> int:
- n = len(coins)
- MAX = amt + 1
- dp = [MAX] * (amt + 1)
- dp[0] = 0
- for i in range(1, n + 1):
- for a in range(1, amt + 1):
- if coins[i - 1] > a:
- dp[a] = dp[a]
- else:
- dp[a] = min(dp[a], dp[a - coins[i - 1]] + 1)
- return dp[amt] if dp[amt] != MAX else -1
解析：答案正确。动态规划状态定义：dp[a]表示凑出金额a所需的最少硬币数，初始化时设为MAX不可达状态）。dp[0] = 0是边界条件，表示金额为0时不需要硬币。状态转移方程：对于每种硬币coins[i-1]，若其面值小于等于当前金额a，则更新dp[a]为min(dp[a], dp[a - coins[i-1]] + 1)。若硬币面值大于 a，则保持dp[a]不变（代码第12-16行）。遍历顺序：外层循环遍历硬币种类（i），内层循环遍历金额（a），确保每种硬币可重复使用（完全背包问题）。若 dp[amt] 未被更新（仍为 MAX），说明无法凑出目标金额，返回 -1；否则返回 dp[amt]。所以代码逻辑正确，符合动态规划解决零钱兑换问题的标准实现。故正确。
3 编程题（每题 25 分，共 50 分）
3.1 编程题1
- 试题名称：学习小组
- 时间限制：3.0 s
- 内存限制：512.0 MB
3.1.1 题目描述
班主任计划将班级里的𝑛名同学划分为若干个学习小组，每名同学都需要分入某一个学习小组中。观察发现，如果一个学习小组中恰好包含𝑘名同学，则该学习小组的讨论积极度为aₖ。
给定讨论积极度a₁, a₂,...,aₙ，请你计算将这𝑛名同学划分为学习小组的所有可能方案中，讨论积极度之和的最大值。
3.1.2 输入格式
第一行，一个正整数𝑛，表示班级人数。
第二行，𝑛个非负整数a₁, a₂,...,aₙ，表示不同人数学习小组的讨论积极度。
3.1.3 输出格式
输出共一行，一个整数，表示所有划分方案中，学习小组讨论积极度之和的最大值。
3.1.4 样例
3.1.4.1 输入样例1
- 4
- 1 5 6 3
3.1.4.2 输出样例1
- 10
3.1.4.3 输入样例2
- 8
- 0 2 5 6 4 3 3 4
3.1.4.4 输出样例2
- 12
3.1.5 数据范围
对于40%的测试点，保证1≤𝑛≤10。
对于所有测试点，保证1≤𝑛≤1000，0≤aᵢ≤10⁴。
3.1.6 编写程序思路
分析：题目是分组优化问题：给定 n 名同学和一组讨论讨论积极度a₁,a₂,...,aₙ（其中aₖ表示一个小组恰好有k名同学时的讨论积极度），目标是将所有同学划分为若干个学习小组（每个小组至少包含 1 名同学），使得所有小组的讨论讨论积极度之和最大。每个同学必须被分配到恰好一个小组中，小组大小k可以是1到n之间的任意整数，且小组大小k对应的讨论积极度aₖ由输入给出（非负整数）。目标函数：最大化所有小组的讨论积极度之和。该问题可以建模为一个完全背包问题："物品" 对应于小组大小k（k=1,2,...,n），每种物品可以无限次使用（即可以创建多个相同大小的小组）；"物品重量" 为小组大小k；"物品价值" 为讨论积极度aₖ。"背包容量" 为总人数n，要求恰好装满背包（所有同学都被分配）。可以使用动态规划（DP）求解，状态定义为：dp[i] 表示分配i 名同学时能获得的最大讨论积极度之和。初始状态：dp[0]=0（0名同学时讨论积极度为0）。状态转移：对于i名同学，枚举最后一个小组的大小k（1≤k≤i），则剩余i−k名同学的最优解为dp[i−k]，因此：
。最终答案为dp[n]。完整参考实现代码如下：
n = int(input()) #同学总数
a = [0] + [int(i) for i in input().split()] #n个不同人数学习小组的讨论积极度。
dp = [0] * (n + 1) #初始化讨论度为0
for i in range(1, n+1): #对每一个同学
for k in range(1, i+1):
dp[i] = max(dp[i], dp[i - k] + a[k]) #状态转移公式
print(dp[n])
3.2 编程题2
- 试题名称：最大因数
- 时间限制：6.0 s
- 内存限制：512.0 MB
3.2.1 题目描述
给定一棵有10⁹个结点的有根树，这些结点依次以1,2,...,10⁹编号，根结点的编号为1。对于编号为k（2≤k≤10⁹）的结点，其父结点的编号为k的因数中除k以外最大的因数。 现在有q组询问，第i（1≤k≤q）组询问给定xᵢ,yᵢ，请你求出编号分别为xᵢ,yᵢ的两个结点在这棵树上的距离。 两个结点之间的距离是连接这两个结点的简单路径所包含的边数。
3.2.2 输入格式
第一行，一个正整数q，表示询问组数。
接下来q行，每行两个正整数xᵢ,yᵢ，表示询问结点的编号。
3.2.3 输出格式
输出共q行，每行一个整数，表示结点xᵢ,yᵢ之间的距离。
3.2.4 样例
3.2.4.1 输入样例1
- 3
- 1 3
- 2 5
- 4 8
3.2.4.2 输出样例1
- 1
- 2
- 1
3.2.4.3 输入样例2
- 1
- 120 650
3.2.4.4 输出样例2
- 9
3.2.5 数据范围
对于60% 的测试点，保证1≤xᵢ,yᵢ≤1000。
对于所有测试点，保证1≤q≤1000，1≤xᵢ,yᵢ≤10⁹。
3.2.6 编写程序思路
分析：题目给出了一棵特殊的树，其节点编号从1到10⁹，根节点为1。对于编号为k（k ≥ 2）的节点，其父节点是k的除k以外最大的因数。例如：节点2的父节点是1（2的因数有1和2，除2外最大是1）；节点3的父节点是1（3的因数有1和3）；节点4的父节点是2（4的因数有1、2、4，除4外最大是2）；节点6的父节点是3（6的因数有1、2、3、6，除6外最大是3）。特点是质数全连在根结点上，质数与根1的距离为1，质数间距离为2。路径长度：如果两个节点x和y在树上的距离是d，那么它们的最近公共祖先（LCA）会出现在路径中。因此，我们可以先找到x和y的LCA，然后计算从x到LCA的距离和从y到LCA的距离，最后相加。如预先计算LCA，则时间复杂度为O(n log n)，对后40%数据会超时。
解决方案：由于树高不超过O(log n)，对n=10⁹树高不超过30。对于每个查询(x, y)，先分别求x、y的节点序列直到根节点，再从分别从x、y开始边计算距离边找它们的LCA，两距离和即为结果。如120：节点序列为120,60,30,15,5,1(最小因素2,2,2,3,5)，650：节点序列为650,325,65,13,1(最小因素2,5,5,13)，LCA为1，120到1的边数为5，650到1的边数为4，故距离为9。
找因素的时间复杂度为O(n¹ᐟ²)，找LCA求距离的时间复杂度O(log n)。总时间复杂度为O(q*n¹ᐟ²*log n))。对60%的数据n≤1000，O(q*n¹ᐟ²*log n))<600*31.63* 9.966=<189135，可忽略；对40%的数据n≤10⁹时O(q*n¹ᐟ²*log n)) <400*32000*30=384000000，10⁸级，基本不会超时。完整参考代码如下：
q = int(input()) #节点组数
def factor(x):
c = [x] #c[0]为初始节点为x，索引大于0为前一个节点的父节点
for i in range(2, int(x**0.5+1e-7)+1): #整数唯一分解定理，因子为不下降序列
while c[-1] % i == 0: #求最小因数i。
c.append(c[-1] // i) #i为最小因素(除以i为最大)，添加前一个节点的父节点
if c[-1] > 1: #最后一个质因素
c.append(1) #添加根节点
return c #节点序列
for i in range(q): #q组节点对
x, y = [int(i) for i in input().split()] #输入两个节点
a = factor(x) #返回a[0]为x节点，其他为其上的父节点直到根节点1
b = factor(y) #返回b[0]为y节点，其他为其上的父节点直到根节点1
px, py = 0, 0
while a[px] != b[py]: #求x、y到最近公共祖先(a[px]==b[py])距离px、py
if a[px] > b[py]:
px += 1
else:
py += 1
print(px + py)
扫一扫
293
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
