四、实现方式
实现方式主要有逐比特计算法、并行计算法和查表法,逐比特计算法有2种方法,第一种是按照标准除法流程进行计算,第二种是按照标准除法等效的移位寄存器进行计算;并行计算法是一次进行多位bit的CRC计算,通过多位bit串联的CRC计算公式得到整个发送序列的CRC;查表法把整个发送序列的CRC值存在一张表中,通过查询即可得到CRC,发送序列太大时需要巨大的存储空间,所以这种方法只适用于发送序列较短的情况,或者可以作为并行计算算法的一部分,在进行多位bit的CRC计算时使用查表法,查表法不再叙述。
a)逐比特计算法
按照标准除法流程进行计算时的算法如下:
(1)在待传输的k比特数据后面加入(n-k)个0,即x^(n-k)M(x)
(2)取x^(n-k)M(x)的前(n-k+1)个数作余式r(x)的初始值
(3)While (数据未处理完),次数为k次
Begin
If (r(x)首位是1)
r(x)= r(x)XOR g(x)
else
r(x)= r(x)
end
r(x)寄存器左移一位,按顺序读入一个新的x^(n-k)M(x)数据于r(x)寄存器的0 bit的位置。
End
(4) r(x)寄存器就是我们所要求的余数。
MATLAB脚本程序如下:
function crc_out = CRC_direct(g,din,InitialState,FinalXOR) %%% g:生成多项式,din:数据输入
lg = length(g); %%%%% g(x)的长度,为n-k+1
ld = length(din); %%%%%%M(x)的长度,为k
din_addzeros = [din;zeros(lg,1)]; %%%%%在待传输的k比特数据后面加入(n-k+1)
%%个0,多加一个是为了为后一步时,r(x)的长度保持为n-k+1
r = din_addzeros(1:lg); %%%%%取x^(n-k)M(x)的前(n-k+1)个数作余式r(x)的初始值
r(1:lg-1) = mod(din_addzeros(1:lg-1) +InitialState.',2) ;%%% r(x)的初始值和输入初始值异或
for ii=1:ld %%%%次数为k次
if r(1) ==0 %%%If (r(x)首位是0)
r(1:lg-1) = r(2:lg); %%% r(x)寄存器左移一位
r(lg)=din_addzeros(ii+lg); %%%%读入一个新的x^(n-k)M(x)数据
else %%%If (r(x)首位是1)
r(1:lg-1) = mod(r(2:lg) + g(2:lg).',2); %%% r(x)= r(x)XOR g(x),首位为0,移除
r(lg)=din_addzeros(ii+lg); %%%%读入一个新的x^(n-k)M(x)数据
end
end
r(1:lg-1) =mod(r(1:lg-1) + FinalXOR.',2); %%%与“结果异或值”进行异或
crc_out = [din;r(1:lg-1)]; %%%组成信息序列和CRC值
按照标准除法等效的移位寄存器进行计算的算法结构如下图所示:
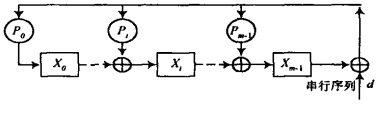

算法流程如下:
(1) 设置CRC寄存器,如果有初值,并给其赋值为“余数初始值”;
(2) 将M(x)的第一个bit 与CRC寄存器最高位进行异或,该结果与g(x)的最低位到次高位进行相乘(g(x)的阶数比CRC高一阶,所以长度与CRC相同),记为rd,CRC寄存器最低位添0,向高位移位,在和rd异或后成为新的CRC寄存器;
(3) M(x)下一个bit进行(2)操作;
(4) M(x)最后一个bit进行(2)操作后,CRC寄存器即为CRC值;
(5) 最终CRC寄存器的内容与“结果异或值”进行或非操作后即为最终的CRC值。





 本文详细介绍了无线通信系统物理层CRC校验的两种实现方式:逐比特计算法(包括标准除法流程和移位寄存器方法)和并行计算法。逐比特法通过逐位处理数据,而并行法则一次处理多位,如16位CRC计算。文中通过算法流程、MATLAB脚本和数学推导进行阐述。
本文详细介绍了无线通信系统物理层CRC校验的两种实现方式:逐比特计算法(包括标准除法流程和移位寄存器方法)和并行计算法。逐比特法通过逐位处理数据,而并行法则一次处理多位,如16位CRC计算。文中通过算法流程、MATLAB脚本和数学推导进行阐述。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 1972
1972

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








