基本可行解

最新推荐文章于 2025-03-19 21:25:46 发布

使君杭千秋

最新推荐文章于 2025-03-19 21:25:46 发布

阅读量5.5k

点赞数 3

分类专栏：凸优化

本文链接：https://blog.youkuaiyun.com/hyl1181/article/details/111970270

版权

凸优化专栏收录该内容

62 篇文章

订阅专栏

线性规划是寻找一组变量使得目标函数达到极小值的问题，其标准形式涉及线性目标函数和线性约束。解分为基本解、基本可行解和最优解，其中基本可行解是满足所有约束的解且变量非负。线性规划若有可行解，必定存在基可行解，最优解存在于这些解中。通过初等行变换，可以将线性规划问题转化为标准形式，进一步求解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

基本概念

线性规划问题的标准形式为：

$\begin{array}{ll} \operatorname{minimize} & c^{T} x \\ \text { subject to } & A x=b \\ & x \succeq 0 \end{array}$

式中： $\boldsymbol{x}=\left[x_{1}, x_{2}, \ldots, x_{n}\right]^{T}, \boldsymbol{c}=\left[c_{1}, c_{2}, \ldots, c_{n}\right]^{T}, \boldsymbol{b}=\left[b_{1}, b_{2}, \ldots, b_{m}\right]^{T}$

$\boldsymbol{A}=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m n} \end{array}\right]$

c^Tx 是目标化函数， Ax=b 称为约束方程， $x\succeq 0$ 为变量非负约束。一般情况下，应有m<n。此时约束方程有无穷多组解，线性规划就是从这无穷多组解中寻找一组使目标函数值最小的最优解。

线性规划问题的约束条件包括约束方程和变量非负约束两部分，对应的解也分基本解、基本可行解和最优解。其中基本解是只满足约束方程的解；基本可行解是同时满足约束方程和变量非负约束的解。基本可行解中能使目标函数值最小的称为最优解。

线性规划问题如果有可行解，则必有基可行解，可行解是基可行解的充分必要条件为：它的非零分量所对应的系数矩阵列向量是线性无关的。基本可行解与可行域中的极点相对应，为有限个。若存在有界最优解，则至少有一个基本可行解为最优解。

基本解的产生和转换

约束方程实际上是一个包含n个变量和m个方程的线性方程组，若令变量中的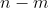 n-m 个等于零，求解方程组得到的解称为线性规划的基本解。

在一个基本解中，称这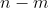 n-m 个为零的变量为非基本变量，称另外的m个变量为基本变量。

系数矩阵和常数向量合并组成增广矩阵：

$\left[\begin{array}{ccccc} a_{11} & a_{12} & \cdots & a_{1 n} & b_{1} \\ a_{21} & a_{22} & \cdots & a_{2 n} & b_{2} \\ \vdots & \vdots & & \vdots & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m n} & b_{m} \end{array}\right]$

对此增广矩阵进行一系列初等行变换，并进行m次消元，可将上述的增广矩阵和约束方程变为：

$\left[\begin{array}{cccccccc} 1 & 0 & \cdots & 0 & a_{1, m+1}^{m} & \cdots & a_{1, n}^{m} & b_{1}^{m} \\ 0 & 1 & \cdots & 0 & a_{2, m+1}^{m} & \cdots & a_{2, n}^{m} & b_{2}^{m} \\ \vdots & \vdots & & \vdots & \vdots & & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & a_{m, m+1}^{m} & \cdots & a_{m, n}^{m} & b_{m}^{m} \end{array}\right]$

故：

$\left[\begin{array}{ccccccc} 1 & 0 & \cdots & 0 & a_{1, m+1}^{m} & \cdots & a_{1, n}^{m} \\ 0 & 1 & \cdots & 0 & a_{2, m+1}^{m} & \cdots & a_{2, n}^{m} \\ \vdots & \vdots & & \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & 1 & a_{m, m+1}^{m} & \cdots & a_{m, n}^{m} \end{array}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right]=\left[\begin{array}{c} b_{1}^{m} \\ b_{2}^{m} \\ \vdots \\ b_{m}^{m} \end{array}\right]$