
作答如下:
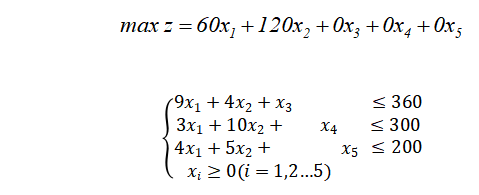
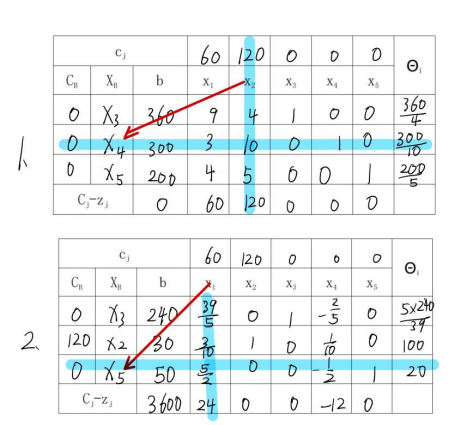
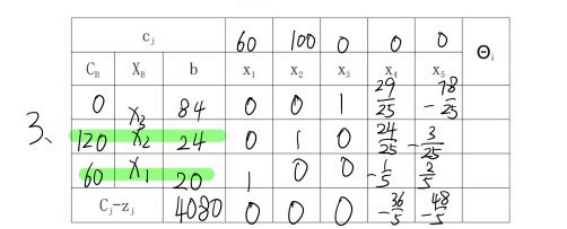
图解法验证:
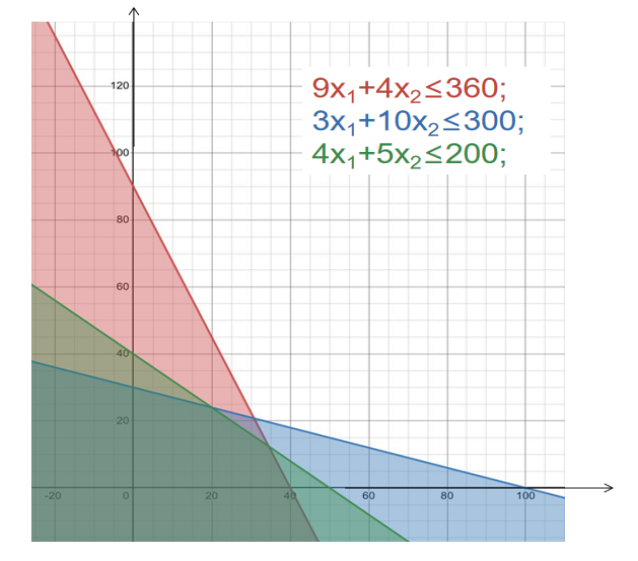
由图可得在点x1=20,x2=24取到最大值Z=4080;
作答如下:
解:
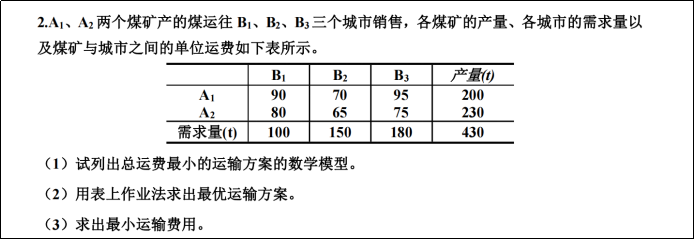
(1)设 xij 为从产地Ai运往销地Bj的运输量,得到下列运输量表设 xij 为从产地Ai运往销地Bj的运输量,得到下列运输量表
|
|
B1 |
B2 |
B3 |
产量 |
|
A1 |
x11 |
x12 |
x13 |
200 |
|
A2 |
x21 |
x22 |
x23 |
230 |
|
销量 |
100 |
150 |
180 |
430 |
模型如下:
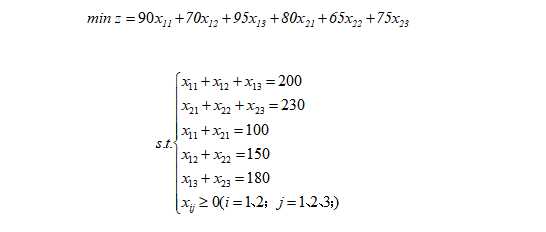
- 采用表上作业法:
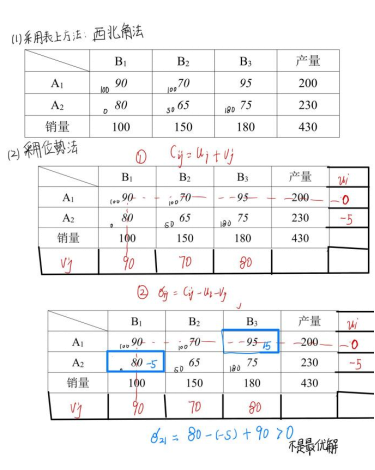
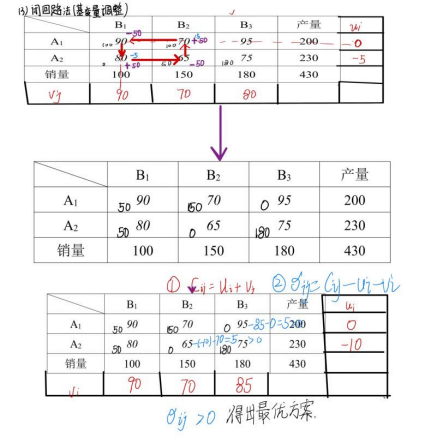
由表上作业法,得到最优方案:A1向B1城市运输50吨,向B2城市运输150吨;A2向B1城市运输50吨,向B3城市运输180吨;
(3)最小运输费用:
利用lingo求解:
运行代码:
min=90*x11+70*x12+95*x13+80*x21+65*x22+75*x23;
x11+x12+x13=200;
x21+x22+x23=230;
x11+x21=100;
x12+x22=150;
x13+x23=180;
x11>0;x12>0;x13>0;
x21>0;x22>0;x23>0;
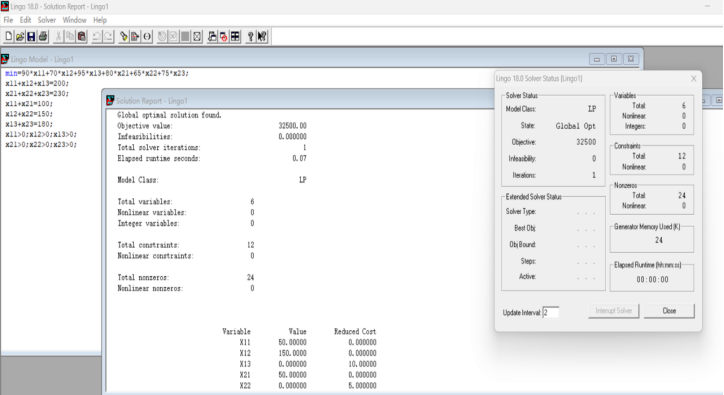
运行结果:
Global optimal solution found.
Objective value: 32500.00
Infeasibilities: 0.000000
Total solver iterations: 1
Elapsed runtime seconds: 0.10
Model Class: LP
Total variables: 6
Nonlinear variables: 0
Integer variables: 0
Total constraints: 12
Nonlinear constraints: 0
Total nonzeros: 24
Nonlinear nonzeros: 0
Variable Value Reduced Cost
X11 50.00000 0.000000
X12 150.0000 0.000000
X13 0.000000 10.00000
X21 50.00000 0.000000
X22 0.000000 5.000000
X23 180.0000 0.000000
Row Slack or Surplus Dual Price
1 32500.00 -1.000000
2 0.000000 0.000000
3 0.000000 10.00000
4 0.000000 -90.00000
5 0.000000 -70.00000
6 0.000000 -85.00000
7 50.00000 0.000000
8 150.0000 0.000000
9 0.000000 0.000000
10 50.00000 0.000000
11 0.000000 0.000000
12 180.0000 0.000000
答:采用以下方法,得到最小运输费用为32500元,即:
A1向B1城市运输50吨,向B2城市运输150吨;A2向B1城市运输50吨,向B3城市运输180吨;
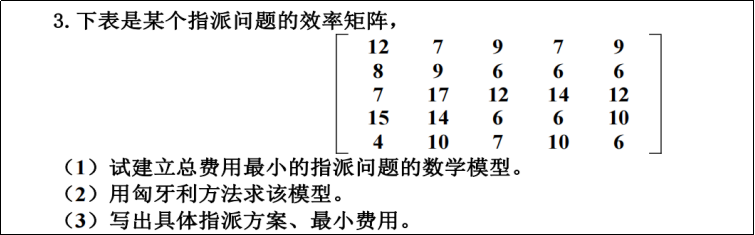
(1)
解:
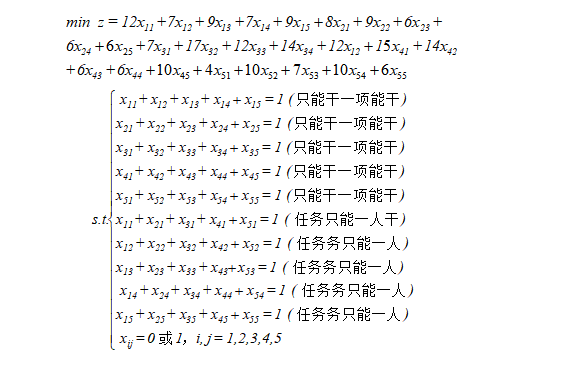
(2)采用匈牙利解法
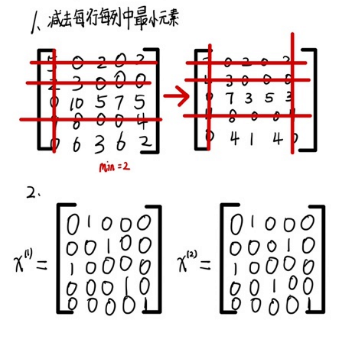
其次可以采用优化的匈牙利解法、具体步骤如下:
step 0:观察每行最小元素个数总和r(sum)和每列最小元素个数总和c(sum)。
step 1:当 r(sum)<=c(sum),则先从系数矩阵的每列减去该列的最小元素,再从所得系数矩阵的每行元素中减去该行的最小元素。反之如果当r(sum)c(sum),则先从系数矩阵的每行减去该行的最小元素,再从所得系数矩阵的每列元素中减去该列 的最小元素。其他步骤同匈牙利法。
- 具体的方案有如下两个,都可以达到最小费用32:
1.甲选择B任务,乙选择C任务,丙选择A任务,丁选择D任务,戊选择E任务;
2.甲选择B任务,乙选择D任务,丙选择A任务,丁选择C任务,戊选择E任务;用lingo进行验证答案一致。

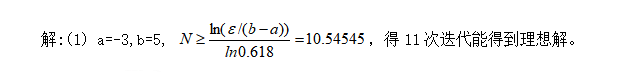




梯度下降法也叫最速下降法,基本思想是往函数下降最快的方向进行搜索,函数某个方向上的变化率可以用函数导数进行表征,因此搜索方向就可以根据函数导数确定,即以 f(x) 在点 xk 方向导数最小的方向作为搜索方向:
利用python程序求解、程序具体见附加:


得出:x1= 3.99996710374836,
x2=1.99997966899839 ,
f(x)极小值分别为 -7.99999999942876
在通过编写MATLAB进行计算,结果如下:x1=4,x2=2时,f(x)=−8,迭代次数为12,与python程序求解一致。
# -*- coding: utf-8 -*-
import sympy as sy
def cal_dffi(f, a, b):
# 声明变量
x1 = sy.symbols("x1")
x2 = sy.symbols("x2")
# 求偏导
f1 = sy.diff(f, x1)
y1 = f1.evalf(subs={x1: a, x2: b})
f2 = sy.diff(f, x2)
y2 = f2.evalf(subs={x1: a, x2: b})
return y1, y2
def gd(a, b, f, alpha, detal):
x1 = sy.symbols("x1") # 声明变量
x2 = sy.symbols("x2")
y0 = f.evalf(subs={x1: a, x2: b}) # 计算函数值
while True:
detalx, detaly = cal_dffi(f, a, b)
a = a - alpha * detalx
b = b - alpha * detaly
y1 = f.evalf(subs={x1: a, x2: b}) # 偏导
if abs(y1 - y0) < detal: # 函数值
break
else:
y0 = y1
return a, b, y1
if __name__ == '__main__':
# 定义函数
x1 = sy.symbols("x1") # 声明变量
x2 = sy.symbols("x2")
f = x1 ** 2 + 2 * x2 ** 2- 2 * x1 * x2 - 4 * x1 # 函数
a = 1 # 初始点
b = 1
alpha = 0.1
detal = 1e-10 # 精度
a, b, y = gd(a, b, f, alpha, detal)
print("x1,x2,f极小值分别为", a, b, y)
6.现有15米长的钢管若干,生产某产品需4米、5米、7米长的钢管各为100、150、120根,问如何截取才能使余料最省?(建立数学模型即可)
作答如下:
这是一个线性规划问题,首先要找出一共有多少中截法;
|
规格/根 序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
7米 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
120 |
|
5米 |
0 |
1 |
0 |
3 |
2 |
1 |
0 |
150 |
|
4米 |
0 |
0 |
2 |
0 |
1 |
2 |
3 |
100 |
|
余料/米 |
1 |
3 |
0 |
0 |
1 |
2 |
3 |
|
建立数学模型: 解:设按第i种方法截xi根(i=1,2,…7);
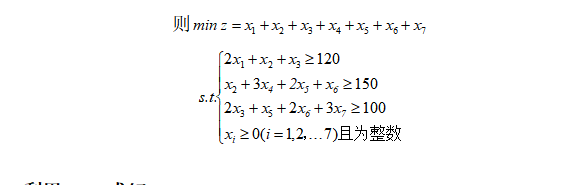
利用lingo求解:
运行代码:
min=x1+x2+x3+x4+x5+x6+x7;
2*x1+x2+x3>=120;
x2+3*x4+2*x5+x6>=150;
2*x3+x5+2*x6+3*x7>=100;
@gin(x1);@gin(x2);@gin(x3);@gin(x4);
@gin(x5);@gin(x6);@gin(x7);
结果:
Global optimal solution found.
Objective value: 135.0000
Objective bound: 135.0000
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 3
Elapsed runtime seconds: 0.11
Model Class: PILP
Total variables: 7
Nonlinear variables: 0
Integer variables: 7
Total constraints: 4
Nonlinear constraints: 0
Total nonzeros: 18
Nonlinear nonzeros: 0
Variable Value Reduced Cost
X1 35.00000 1.000000
X2 0.000000 1.000000
X3 50.00000 1.000000
X4 50.00000 1.000000
X5 0.000000 1.000000
X6 0.000000 1.000000
X7 0.000000 1.000000
Row Slack or Surplus Dual Price
1 135.0000 -1.000000
2 0.000000 0.000000
3 0.000000 0.000000
4 0.000000 0.000000
答:使用135根15米长的钢管,采用以下方案,余料最省:
取35根使用第一种法得到70根7米长的钢管,剩余余料35米;
取50根使用第四种法得到150根5米长的钢管,剩余余料0米;
取50根使用第三种法得到50根7米长、100根4米长的钢管,剩余余料0米;
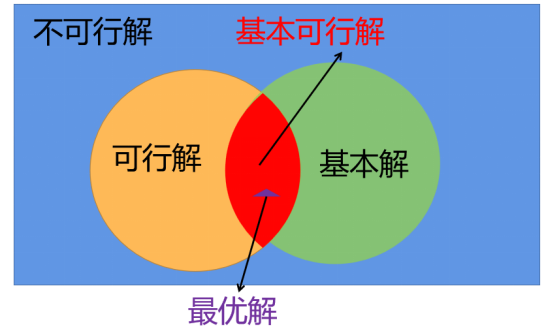
- 请结合实例解释线性规划问题的基本(不可行)解,基本可行解,可行解(不是基本解),并说明三者之间关系。
结合生产计划用一张图,来举例分析线性规划问题的三种解:
生产计划问题:结合下列表格,如何安排生产使利润最大?
|
|
Ⅰ |
Ⅱ |
资源 |
|
设备 |
5 |
2 |
170 |
|
原材料A |
2 |
3 |
100 |
|
原材料B |
1 |
5 |
150 |
|
利润 |
10 |
18 |
|
采用图解法:
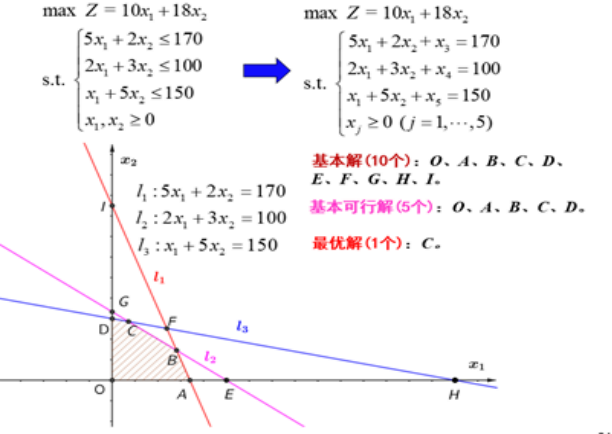
基本解:各个等式约束直线的交点,外加与坐标轴的交点
基本可行解:基本解里面在可行域范围的那些基本解,可行域的顶点
可行解:可行解只有一个要求:满足所有约束条件
最优解:基本可行解里面使目标函数最大(最小)的基本可行解
解之间的关系如下图:







 文章通过运输问题和生产计划展示了线性规划的解决过程,利用lingo软件求解最小运输费用和钢管截取问题,同时提到了梯度下降法在函数极小化中的应用。
文章通过运输问题和生产计划展示了线性规划的解决过程,利用lingo软件求解最小运输费用和钢管截取问题,同时提到了梯度下降法在函数极小化中的应用。


















 1618
1618

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










