凸优化第九章无约束优化 9.4 最速下降方法

最新推荐文章于 2024-01-02 00:02:09 发布

使君杭千秋

最新推荐文章于 2024-01-02 00:02:09 发布

阅读量576

点赞数 1

分类专栏：凸优化

原文链接：https://blog.youkuaiyun.com/wangchy29/article/details/88121255

版权

凸优化专栏收录该内容

62 篇文章

订阅专栏

9.4 最速下降方法

对f(x+v)在x处进行一阶Taylor展开：

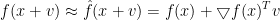
$f(x+v)\approx \hat{f}(x+v)=f(x)+\bigtriangledown f(x)^Tv$

其中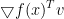 $\bigtriangledown f(x)^Tv$ 是f在x处沿方向v的方向导数

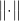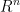令 $\begin{Vmatrix}\cdot \end{Vmatrix}$ 是 R^n 上的任意番薯，顶一个规范化的最速下降方向：

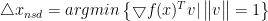
$\bigtriangleup x_{nsd}=argmin\left \{ \bigtriangledown f(x)^Tv|\begin{Vmatrix} v\end{Vmatrix} =1\right \}$

一个规范化的最速下降方向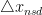 $\bigtriangleup x_{nsd}$ 是一个能使f的线性近似下降最多的具有单位范数的步径。

也可以将规范化的最速下降方向乘以一个特殊的比例因子，从而考虑下述非规范化的最速下降方向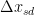 $\Delta x_{sd}$ ：

$\Delta x_{sd}=\begin{Vmatrix} \bigtriangledown f(x)\end{Vmatrix}_*\bigtriangleup x_{nsd}$

其中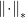 $\left \| \cdot \right \|_*$ 表示对偶范数。对于这种最速下降步径，有：

$\bigtriangledown f(x)^T\bigtriangle x_{sd}=\left \| \bigtriangledown f(x) \right \|_*\bigtriangle f(x)^T\bigtriangleup x_{nsd}=-\left \| \bigtriangledown f(x) \right \|_*^2$

不同范数下的最速下降方法

采用Euclid范数的最速下降方法

此时最速下降方向就负梯度方向，也就是梯度下降方法。

采用二次范数的最速下降方法

考虑二次范数

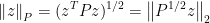
$\left \| z \right \|_P=(z^TPz)^{1/2}=\left \| P^{1/2} z \right \|_2$

其中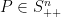 $P \in S_{++}^n$ 。此时规范化的最速下降方向：

$\bigtriangleup x_{nsd}=-(\bigtriangledown f(x)^TP^{-1}\bigtriangledown f(x))^{-1/2}P^{-1}\bigtriangledown f(x)$

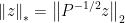对偶范数 $\left \| z \right \|_*=\left \| P^{-1/2}z \right \|_2$ 。因此在二次范数下的最速下降步径为：

$\Delta x_{sd}=-P^{-1}\bigtriangledown f(x)$

基于坐标变换的解释

对于最速下降方向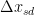 $\Delta x_{sd}$ ，还有另一种解释：即对原问题进行某种坐标变换后的梯度下降方向。

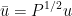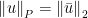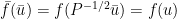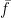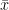定义 $\bar{u}=P^{1/2}u$ ，于是 $\left \| u \right \|_P=\left \| \bar{u} \right \|_2$ ，采用这种坐标变换，原目标函数f的极小化问题可以等价为极小化下式给出的目标函数 $\bar{f}(\bar{u})=f(P^{-1/2}\bar{u})=f(u)$ 。此时采用梯度下降方法优化 $\bar{f}$ ，在点 $\bar{x}$ 处的直线搜索方向为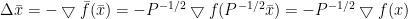： $\Delta \bar{x}=-\bigtriangledown \bar{f}(\bar{x})=-P^{-1/2}\bigtriangledown f(P^{-1/2}\bar{x})=-P^{-1/2}\bigtriangledown f(x)$

而对应于原变量x的直线搜索方向：

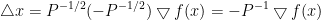
$\bigtriangleup x = P^{-1/2}(-P^{-1/2})\bigtriangledown f(x)=-P^{-1}\bigtriangledown f(x)$

也就是说在二次范数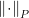 $\left \| \cdot \right \|_P$ 下的最速下降方向，可以理解为对原问题进行最标编号 $\bar{x}=P^{1/2}x$ 后的梯度方向。

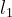范数下的最速下降方向

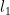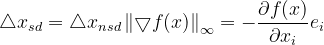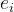l_1 范数下的最速下降方向： $\bigtriangleup x_{sd}=\bigtriangleup x_{nsd}\left \| \bigtriangledown f(x) \right \|_{\infty}=-\frac{\partial f(x)}{\partial x_i}e_i$ ，其中 e_i 表示第i个标准基向量。可以理解为每次得到一个梯度，这个梯度中有不同的分量，每个分量有不同的大小，每次都选择值最大的那个分量的方向来更新。

最速下降方向的范数选择

如上图是两个同一个问题不同的范数下的得到的迭代过程，可以看出左图范数下，收敛速度快，这是因为当考虑坐标变换的时候，最速下降法变成了梯度下降方法，而在这种变换下，下水平集的条件数被减小了，而梯度下降方法的收敛速度与下水平集的条件数有关，条件数减少了收敛速度也就快了，而右图收敛速度慢，是因为在这种坐标变换下，下水平集的条件数增多了。

来源：https://blog.youkuaiyun.com/wangchy29/article/details/88121255