树状数组基础

树状数组，又称二进制索引树，英文名Binary Indexed Tree。

树状数组用来求区间元素和，求一次区间元素和的时间效率为O(logn)。
有些同学会觉得很奇怪。
用一个数组S[i]保存序列A[]的前i个元素和，那么求区间i,j的元素和不就为S[j]-S[i-1]，那么时间效率为O(1)，岂不是更快？
但是，如果题目的A[]会改变呢？
例如：我们来定义下列问题：我们有n个盒子。
可能的操作为：
1.查询从盒子i到盒子j总的石块数
2.向盒子k添加石块
操作1为O(1)的复杂度，S[j]-S[i-1即可。
而对操作2为O(n)的时间复杂度，需要更新s[k]到s[n]。
但是用树状数组，对操作1和2的时间复杂度都为O(logn)。
先上图

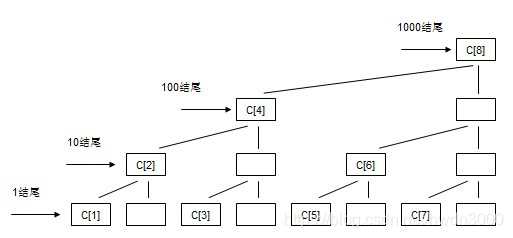
若区间的结尾为R，则区间长度就等于R的二进制分解下的最小二次幂，即lowbit（R）
例如x=7=2²+2¹+2⁰
lowbit(7)=1,也就是C[7]区间有一个数A[7]
右区间是7，区间长度是lowbit(7),那么左区间就是R-lowbit（R）+1

//lowbit：从右往左第一个1的位置
int lowbit(int x){	return x&-x;}

下面的代码可以计算出区间[1,x]分成几个小区间

while(x>0)
{
cout<<x-lowbit(x)+1<<" "<<x<<endl;
x-=lowbit(x);
}

对于给定的序列a，我们建立一个数组c，其中c[x]保存序列a的区间[x-lowbit(x)+1,x]中所有数的和。

例如a[1]~a[8]
c[8] 右区间为8， 8-lowbit（8）+1=1是左区间，也就是c[8]代表
a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]这8个数的和。
如果求前8个元素的前缀和，那么c[8]就是

树状数组求前缀和的代码

int ask(int x)//为右区间，左区间默认为1
{
int ans=0;
while(x>0)
{
ans+=c[x];
x-=lowbit(x);
}
return ans;
}

int ask(int x）函数就是求x的前缀和，当x=8，ans+=c[8]
执行x=x-lowbit（8）x=0，循环退出。c[8]这个区间长度为8（区间长度由lowbit（8）求出)，正好是a[1]~a[8]的和。

ask(7)表示求前7个数组元素的和
ans=ans+c[7];
执行x=7-lowbit(7) x=6
ans=ans+c[6] ;
执行x=6-lowbit（6) x=4
ans=ans+c[4];
执行x=4-lowbit（4） x=0
循环退出。
也就是前7个元素的前缀和就是c[7]+c[6]+c[4]这几个小区间的和

c[7]的区间长度为lowbit（7）=1, 右区间为7，左区间为7-lowbit(7)+1=7,也就是c[7]的区间是[7,7]只包含一个a[7]
c[6]的区间长度为lowbit(6)=2 ,右区间为6，左区间为6-lowbit(6)+1=5，也就是c[6]的区间为[5,6],它有a[5]、a[6]的和。
c[4]的区间长度为lowbit(4)=4, 右区间为4，左区间为4-lowbit(4)+1=1, 也就是c[4]的区间为[1,4]，它有a[1]、a[2]、a[3]、a[4]的和。

通过上面的分析，我们知道ask(7)有c[7]、c[6]、c[4]三个小区间的和组成。
c[7]=a[7]
c[6]=a[6]+a[5]
c[4]=c[4]+c[3]+c[2]+c[1]
我们已经知道树状数组c[]是这样构成的，我们怎么初始化一个树状数组
如果使用下面的代码

//树状数组初始化
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int n=8;
int a[n+1]={0,1,2,3,4,5,6,7,8};
int c[n+1];
int lowbit(int x)
{
 return x&-x;
 } 
int ask(int x)
{
 int ans=0;
 while(x>0)
 {
  ans+=c[x];
  x-=lowbit(x);
 }
 return ans;
 } 
 int main()
 {
   for(int x=1;x<=n;x++)
   {
    int r=x;
    int l=x-lowbit(x)+1;
    while(r>=l) //r-lowbit(r)+1 为左区间
     {
       c[x]+=a[r];
       r--;
     } 
   }
   for(int x=1;x<=n;x++)
   printf("%d ",c[x]);
   printf("\n");
   printf("%d\n",ask(4)); 
   return 0;
 }

上面的代码在初始化树状数组c[ ]时，用到了循化的嵌套O（n²)，这是不可取得，我们使用树状数组的目的就是为时间复杂度位O（log n）

用O（log n）的方法初始化树状数组

//用树状数组单点增加来初始化
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int n=8;
int a[n+1]={0,1,2,3,4,5,6,7,8};
int c[n+1];
int lowbit(int x)
{
 return x&-x;
 } 
void add(int x,int y)//单点增加
{
 for(;x<=n;x+=lowbit(x))
 c[x]+=y;
}
int ask(int x)//求前缀和
{
 int ans=0;
 for(;x;x-=lowbit(x))
 ans+=c[x];
 return ans;
}
 int main()
 {
   for(int x=1;x<=n;x++)
   {
    add(x,a[x]); 
   }
   for(int x=1;x<=n;x++)
   printf("%d ",c[x]);
   printf("\n");
   printf("%d\n",ask(4)); 
   return 0;
 }