树状数组基础篇

最新推荐文章于 2023-08-12 00:17:53 发布

laruat

最新推荐文章于 2023-08-12 00:17:53 发布

阅读量221

点赞数

CC 4.0 BY-SA版权

分类专栏：日常文章标签：算法 c++

本文链接：https://blog.youkuaiyun.com/SSL_hhw/article/details/112393532

日常专栏收录该内容

28 篇文章

订阅专栏

树状数组是一种数据结构，用于高效处理数列的动态修改和区间查询。它以二分方式构造，修改和查询复杂度均为O(logN)。与线段树相比，树状数组在空间和时间上更优，且代码简洁。文章介绍了树状数组的定义、区间划分、单点增加操作及前缀和查询，并提供了一个实际应用例子。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

树状数组基础篇

*大家可以先了解一下—>线段树

引入

数列操作:
给定一个初始值都为0的序列,动态地修改一些位置上的数字,加上一个数,减去一个数,或者乘上一个数,然后动态地提出问题,问题的形式是求出一段数字的和.

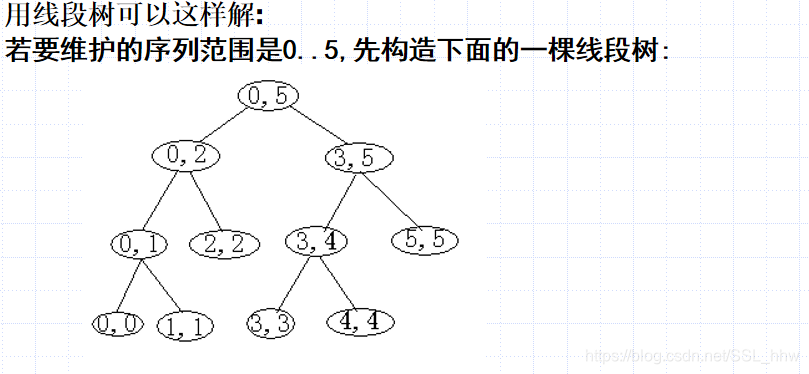
在这里插入图片描述

1.可以看出,这棵树的构造用二分便可以实现.复杂度是logN.
2.每个结点用数组a来表示该结点所表示范围内的数据之和.
3.修改一个位置上数字的值,就是修改一个叶子结点的值,而当程序由叶子结点返回根节点的同时顺便修改掉路径上的结点的a数组的值.
4.对于询问的回答,可以直接查找i…j范围内的值,遇到分叉时就兵分两路,最后再合起来.也可以先找出0…i-1的值和0…j的值,两个值减一减就行了.后者的实际操作次数比前者小一些.
5.这样修改与维护的复杂度是logN.询问的复杂度也是logN,对于M次询问,复杂度是MlogN.

这个东西，对于线段树来说是一个时间和空间上的飞跃，在空间上，最多只要开到原数组的2倍，而线段树要四倍，在时间上也略快于线段树。（最重要是代码短，懒人的福音）
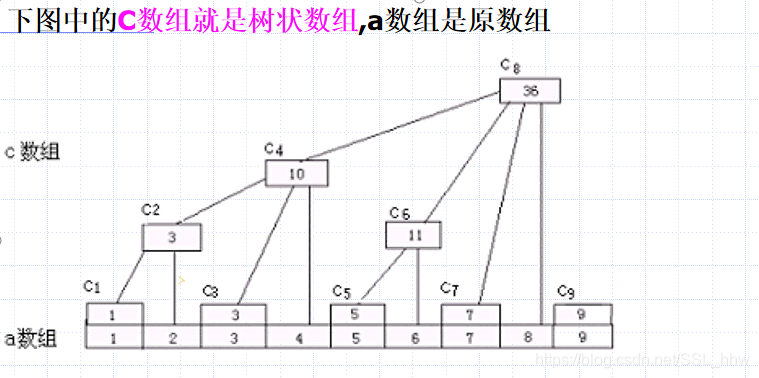
在这里插入图片描述
问题：区间是如何划分的

对于序列a，我们设一个数组C定义C[i] = a[i – 2^k + 1] + … + a[i]，k为i在二进制下末尾0的个数
K的计算可以这样: 2^k=x & (-x)
Examply 以6为例
(6)10=(0110)2
(-6)10=(1010)2
6 & -6=2

结构看上去要比线段树复杂，实际~~~~很短（相对于线段树）

敲重点它的原理

我们定义lowbit(n)=n&(-n)表示取出非负整数n在二进制表示下最低位的1以及它后边的0构成的数值
c[x]保存序列A的区间[x- lowbit(x)+1，x]中所有数的和。
该结构满足以下性质:
1.每个内部节点c[x]保存以它为根的子树中所有叶节点的和。
2.每个内部节点c[x]的子节点个数等于 lowbit(x)的大小。
3.除树根外，每个内部节点c[x]的父节点是c[x+ lowbit(x)]。
4.树的深度为O(logN)

运用

1.对某个元素进行加法操作

树状数组支持单点增加，意思是给序列中的某个数A[x]加上y，同时正确维护序列的前缀和。根据上面给出的树形结构和它的性质，只有节点c[x]及其所有祖先节点保存的“区间和”包含A[x]，而任意一个节点的祖先至多只有logN个，我们逐一对它们的c值进行更新即可。下面的代码在O(logN)时间内执行单点增加操作。

void update(int x, int y) 
{
	for (; x <= N; x += x & -x) c[x] += y;
}
///////////////////////////////////////////
void update(int x, int y) 
{
	while(x<=n)  c[x]=c[x]+y,x=x+x&-x;           
}

以上两种写法等效。

2.查询前缀和

树状数组支持查询前缀和，即序列A第1~x个数的和。按照我们刚才提出的方法，应该求出x的二进制表示中每个等于1的位，把[1，x]分成O(logN)个小区间，而每个小区间的区间和都已经保存在数组c中。下面的代码在O(logN)时间内查询前缀和:

int sum(int x) 
{
	int ans = 0;
	for (; x; x -= x & -x) ans += c[x];
	return ans;
}

大家可以尝试一下例题POJ P2352 Stars

Stream of thoughts

对于每个星星按y坐标从小到大排序，相同y坐标按x坐标从小到大排序。输入顺序已排好序，那么只要依次统计星星i之前x坐标小于等于i.x的星星有多少，即是星星i的级别。y坐标没用，显然是一维树状数组应用。
　　设数组a[x]初始为0，表示在x坐标处星星的个数，则求和a[0] ~ a[x]则为该星星的等级。
有一个地方尤其要注意，树状数组是以1号为起始的，而且只能用1号。x可能为0，为0会时陷入死循环，处理时要将所有的x+1。
还有就是x的范围不能事先确定，在update的时候直接加到x取值范围的最大值，即32001，或者在输入的时候找一个x的最大值。

以下是AC代码

#include<iostream>
#include<cstdio>
#define N 32001 
#define M 15001
using namespace std;
int n,m;
int x[M],y,tr[N],an[M];
inline int lt(int t){return t&(-t);}
void add(int x){ for(;x<=m;x+=lt(x)) tr[x]++; }
int sum(int x)
{
	int ans=0;
	for(;x;x-=lt(x)) ans+=tr[x];
	return ans;
}
int ma(int a,int b){return a>b?a:b;}
int main()
{
	scanf("%d",&n);
	for(register int i=1;i<=n;i++)
	 {
	 	scanf("%d%d",&x[i],&y);
	 	x[i]++;
	 	m=ma(m,x[i]);
	 }
	for(register int i=1;i<=n;i++) add(x[i]),an[sum(x[i])]++;
	for(register int i=1;i<=n;i++) printf("%d\n",an[i]);
    return 0;	
}