本文介绍马氏距离(Mahalanobis Distance),通过本文,你将了解到马氏距离的含义、马氏距离与欧式距离的比较以及一个通过马氏距离进行异常检测的例子(基于Python的sklearn包)。
目的
计算两个样本间的距离时,需要考虑样本所在的分布造成的影响。影响包括两个方面:
- 不同维度上的方差不同,进而不同维度在计算距离时的重要性不同;
- 不同维度间可能存在相关性,干扰距离计算。
当数据的分布已知时,我们通常会用马氏距离代替欧氏距离,或者选择另一种方法:对数据进行转换(如PCA)。
定义
- 度量样本到样本分布间的距离
d = ( x ⃗ − μ ⃗ ) T S − 1 ( x ⃗ − μ ⃗ ) d = \sqrt{(\vec x - \vec \mu)^T S^{-1} (\vec x - \vec \mu)} d=(x−μ)TS−1(x−μ)其中 μ ⃗ \vec \mu μ是样本分布的均值, S S S是样本分布的协方差矩阵 - 度量一个分布下,两个样本之间的距离
d = ( x ⃗ − y ⃗ ) T S − 1 ( x ⃗ − y ⃗ ) d = \sqrt{(\vec x - \vec y)^TS^{-1}(\vec x - \vec y)} d=(x−y)TS−1(x−y)
直观理解
下面是一个二维空间中距离度量的例子(戳这里查看实例来源)。
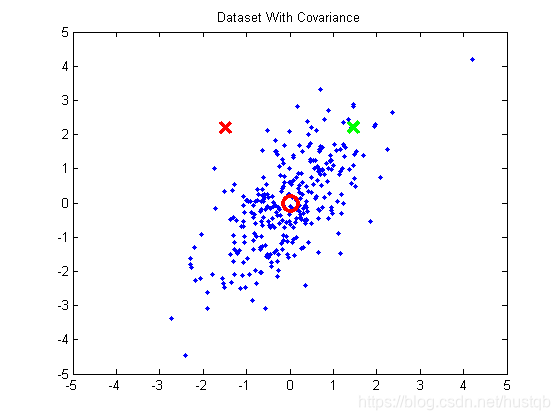
图中,圆圈表示样本分布的中心点 c c c,两个叉分别表示两个样本点 x , y x, y x,y,从图中可以看出,在二维空间中两个叉到样本分布的中心点间的欧氏距离相等。但是很明显,绿叉应该是分布内的点,红叉是分布外的点,所以绿叉距离分布中心点的距离应该更近才合理。
使用马氏距离,就等同于通过数据转换的方法,消除样本中不同特征维度间的相关性和量纲差异,使的欧式距离在新的分布上能有效度量样本到分布间的距离。
-
第一步,端详一下原始数据分布的特点。
这些样本的特征维度即为横坐标轴和纵坐标轴,且两个特征维度呈现明显的正相关性。 -
第二步,消除不同维度之间的相关性。
消除特征维度间的相关性后,样本分布图如下所示,还存在的一个问题是两个特征维度间的量纲不一致。
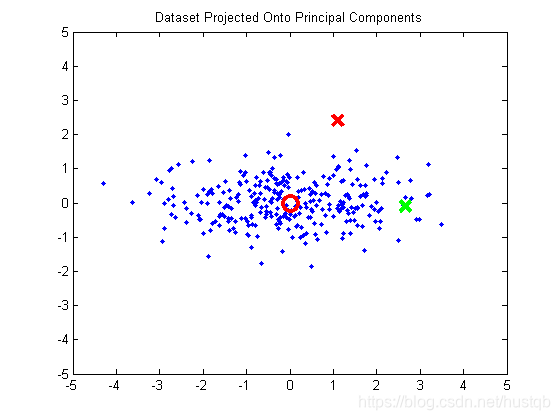
- 第三步,消除不同维度之间的量纲差异。
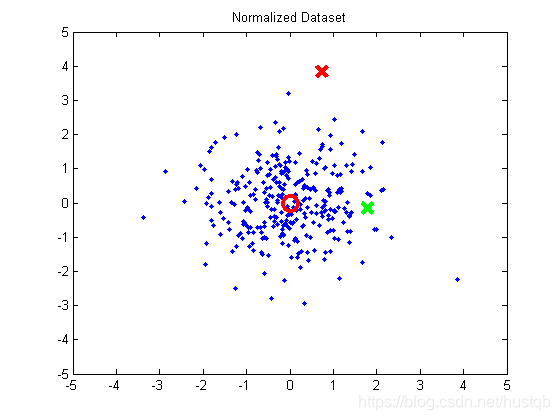
经过以上三步,现在的样本分布下,样本间的距离可以用欧氏距离来衡量。
性质
马氏距离消除了样本不同维度之间的方差差异和相关性,是一个无量纲的度量方式。
与欧式距离的关系
- 如果协方差矩阵是单位矩阵 → \rightarrow →样本的特征维度间相关性(协方差)为0,量纲一致 → \rightarrow →马氏距离等同于欧氏距离。
- 如果协方差矩阵是对角矩阵 → \rightarrow →样本的特征维度间的量纲一致 → \rightarrow →马氏距离等同于标准化后的欧氏距离。
实例——用马氏距离进行异常检测
实例来自sklearn官方文档
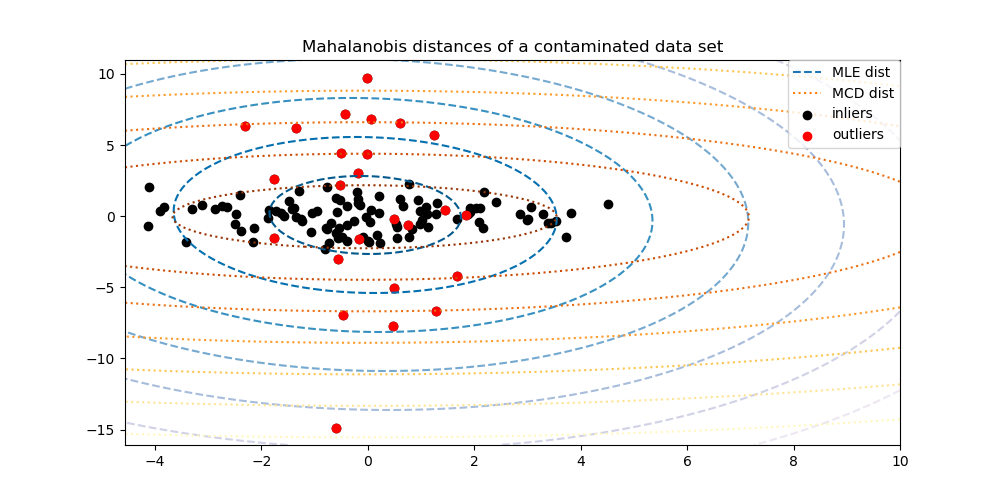





 本文深入探讨了马氏距离的概念,解释了为何在处理具有不同方差和相关性的数据时,它比欧式距离更具优势。通过一个具体的Python sklearn实现的异常检测例子,阐述了如何利用马氏距离来识别分布外的样本。
本文深入探讨了马氏距离的概念,解释了为何在处理具有不同方差和相关性的数据时,它比欧式距离更具优势。通过一个具体的Python sklearn实现的异常检测例子,阐述了如何利用马氏距离来识别分布外的样本。

















 2657
2657

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








