【关于通用六轴机械臂的动力学最小集参数】

原创已于 2022-09-28 08:30:03 修改 · 3.2k 阅读

49 ·

CC 4.0 BY-SA版权

于 2022-09-27 10:54:43 首次发布

机械臂动力学专栏收录该内容

2 篇文章

订阅专栏

本文详细介绍了使用牛顿欧拉公式、线性分离形式和最小参数集三种方法求解六轴通用机械臂的关节力矩，并通过MATLAB仿真验证了各方法的准确性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在我做动力学仿真来求解通用六轴机械臂的关节力矩时候，用牛顿欧拉公式以及线性分离形式都能求出关节力矩与matlab自带的仿真环境Simmechanics做对比，结果ok，但实际用最小参数集来求解关节力矩仿真时，遇到了前所未有的困难，在网上，我所能查得到的资料中，几乎很少有人能把所有的最小集参数写完整，或者说他们写的不对，也有些是莫名其妙的参数，但是结果是对的，也挺奇怪，这里我将写出通用六轴机械臂的最小集，这里的通用六轴机械臂指的是456轴轴线交于一点的六轴工业机械臂。关于理论的基础大家可以参考《机器人动力学与控制》这本书。书本上能写出4、5、6轴的最小参数集，但是1、2、3轴如果完全套用书上公式，那结果完全得到的会有问题。

这里先写出通用机械臂的修改dh模型，注意，这里最好是修改的dh模型，《机器人动力学与控制》这里面绝大多数最小集参数都是由修改dh模型写出来的。根据建立的坐标系可以得到修改dh参数表：

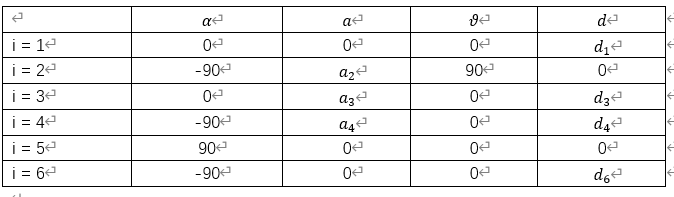
根据牛顿欧拉公式：

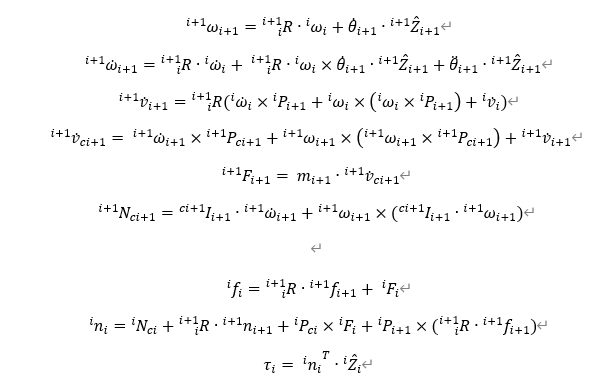
先根据牛顿欧拉方法可以验证出matlab与牛顿欧拉公式的正确性。Matlab程序如下：

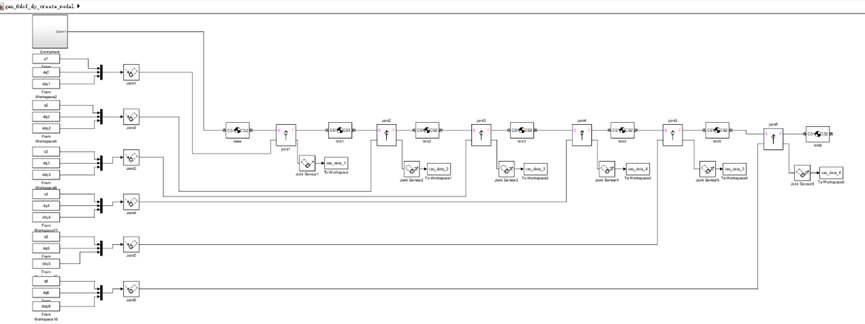
我这里用的是Simmechanics的第一代，Matlab版本是2015b，做的也比较简单，但是不影响结果，网上也有些朋友用的是admas，这里没有要求，笔者这里用matlab比较习惯，就用matlab了。

Matlab的牛顿欧拉公式如下：在求取力矩之前，需要先生成机器人本体参数及运动轨迹参数：

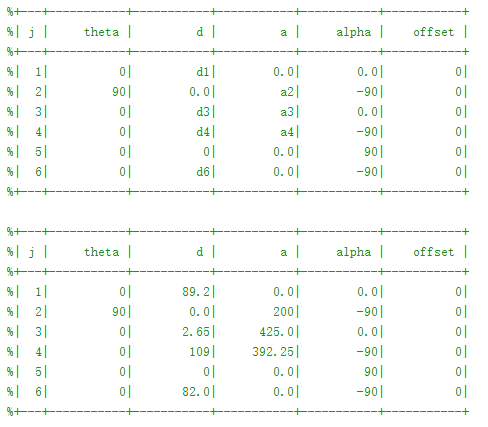
clc;
clear;
global Ts ;
Ts = 0.01;
total_time = 10.0;
t = 0:Ts:total_time;
le = length(t);
zero = zeros(1,le);
format long g;
pos1 = 0.4*sin(t)*180.0/pi; vel1 = 0.4*sin(t+pi/2)*180.0/pi; acc1 = 0.4*sin(t+pi)*180.0/pi;
pos2 = 1.2*pos1; vel2 = 1.2*vel1; acc2 = 1.2*acc1;
pos3 = 1.5*pos1; vel3 = 1.5*vel1; acc3 = 1.5*acc1;
pos4 = 2.0*pos1; vel4 = 2.0*vel1; acc4 = 2.0*acc1;
pos5 = -2.0*pos1; vel5 = -2.0*vel1; acc5 = -2.0*acc1;
pos6 = 2.5*pos1; vel6 = 2.5*vel1; acc6 = 2.5*acc1;
% 生成轨迹参数,给定每个轴为正弦曲线形式;
q1 = [t',pos1']; dq1 = [t',vel1']; ddq1 = [t',acc1'];
q2 = [t',pos2']; dq2 = [t',vel2']; ddq2 = [t',acc2'];
q3 = [t',pos3']; dq3 = [t',vel3']; ddq3 = [t',acc3'];
q4 = [t',pos4']; dq4 = [t',vel4']; ddq4 = [t',acc4'];
q5 = [t',pos5']; dq5 = [t',vel5']; ddq5 = [t',acc5'];
q6 = [t',pos6']; dq6 = [t',vel6']; ddq6 = [t',acc6'];
% 打开某个轴就可以让某些轴停转，验证simulink仿真里面的模型是否正确; 
% q1 = [zero',zero']; dq1 = [zero',zero']; ddq1 = [zero',zero'];
% q2 = [zero',zero']; dq2 = [zero',zero']; ddq2 = [zero',zero'];
% q3 = [zero',zero']; dq3 = [zero',zero']; ddq3 = [zero',zero'];
% q4 = [zero',zero']; dq4 = [zero',zero']; ddq4 = [zero',zero'];
% q5 = [zero',zero']; dq5 = [zero',zero']; ddq5 = [zero',zero'];
% % q6 = [zero',zero']; dq6 = [zero',zero']; ddq6 = [zero',zero'];
%
global g m1 m2 m3 m4 m5 m6;
global a2 a3 a4 d1 d3 d4 d6;
global ic1xx ic1xy ic1xz ic1yy ic1yz ic1zz ic2xx ic2xy ic2xz ic2yy ic2yz ic2zz ic3xx ic3xy ic3xz ic3yy ic3yz ic3zz;
global ic4xx ic4xy ic4xz ic4yy ic4yz ic4zz ic5xx ic5xy ic5xz ic5yy ic5yz ic5zz ic6xx ic6xy ic6xz ic6yy ic6yz ic6zz;
global pc1x pc1y pc1z pc2x pc2y pc2z pc3x pc3y pc3z pc4x pc4y pc4z pc5x pc5y pc5z pc6x pc6y pc6z;
global ic1 ic2 ic3 ic4 ic5 ic6;
global Pc111 Pc222 Pc333 Pc444 Pc555 Pc666;
global P001 P112 P223 P334 P445 P556 P667;
global ii1 ii2 ii3 ii4 ii5 ii6 U_r;
g = 9.8065;
a2 = 100.0/1000.0;
d4 = 425.0/1000.0;
a4 = 92.430/1000.0;
d1 = 89.2/1000.0;
d3 = 2.650/1000.0;
a3 = 409/1000.0;
d6 = 82.0/1000.0;
m1 = 4.43412756; m2 = 16.84660904; m3 = 4.60251258; m4 = 0.47079045;m5 = 0.07740646;m6 = 0.00343612;
 %这里的参数可以根据实际情况来写，我这里直接拿的别的机械手参数过来用的;
ic1xx = 27327.74254539/1e6; ic1xy = 0.01004954/1e6; ic1xz = -0.00779330/1e6; ic1yy = 13316.18396352/1e6; ic1yz = 278.53998863/1e6; ic1zz = 27164.17826539/1e6;
ic2xx = 97229.72023998/1e6; ic2xy = 7.88590602/1e6; ic2xz = 4347.46076297/1e6; ic2yy = 596573.36974102/1e6; ic2yz = 48.38291302/1e6; ic2zz = 659758.11150989/1e6;
ic3xx = 82615.26803540/1e6; ic3xy = -0.48370451/1e6; ic3xz = -0.36529045/1e6; ic3yy = 9191.62918392/1e6; ic3yz = -2.27394513/1e6; ic3zz = 87354.59533550/1e6;
ic4xx = 772.88609433/1e6; ic4xy = 0.0;  ic4xz = 0.0; ic4yy = 737.71865597/1e6; ic4yz = 0.0; ic4zz = 466.83449961/1e6;
ic5xx = 43.03191218/1e6; ic5xy = 0.00000113/1e6; ic5xz = -0.00001206/1e6; ic5yy = 16.96626524/1e6;  ic5yz = 0.0; ic5zz = 45.41353352/1e6;
ic6xx = 0.16156936/1e6; ic6xy = -0.00000078/1e6; ic6xz = 0.00002638/1e6; ic6yy = 0.16156919/1e6; ic6yz = -0.00003322/1e6; ic6zz = 0.13635579/1e6;
pc1x = 0.0;  pc1y = 22.50469351/1e3; pc1z = -2.79144309/1e3;
pc2x = 82.73652456/1e3; pc2y = -0.04677543/1e3; pc2z = 75.58039753/1e3;
pc3x = -0.00117880/1e3; pc3y = 88.77417776/1e3; pc3z = -10.15843771/1e3;
pc4x = 0.00;  pc4y = 0.0; pc4z = -32.40904555/1e3;
pc5x = 0.00; pc5y = 10.97413693/1e3; pc5z = 0.0;
pc6x = -0.00143273/1e3; pc6y = 0.00162829/1e3; pc6z = -1.68591556/1e3;
Pc111 = [pc1x pc1y pc1z]';Pc222 = [pc2x pc2y pc2z]';Pc333 = [pc3x pc3y pc3z]';Pc444 = [pc4x pc4y pc4z]';Pc555 = [pc5x pc5y pc5z]';Pc666 = [pc6x pc6y pc6z]';
P001 = [0 0 d1]';P112 = [a2 0 0]';P223 = [a3 0 d3]';P334 = [a4 d4 0]';P445 = [0 0 0]';P556 = [0 d6 0]'; P667 = [0 0 0]'; 
ic1=[ic1xx -ic1xy -ic1xz;
 -ic1xy ic1yy -ic1yz;
 -ic1xz -ic1yz ic1zz]; 
ic2=[ic2xx -ic2xy -ic2xz;
 -ic2xy ic2yy -ic2yz;
 -ic2xz -ic2yz ic2zz];
ic3=[ic3xx -ic3xy -ic3xz;
 -ic3xy ic3yy -ic3yz;
 -ic3xz -ic3yz ic3zz]; 
ic4=[ic4xx -ic4xy -ic4xz;
 -ic4xy ic4yy -ic4yz;
 -ic4xz -ic4yz ic4zz];
ic5=[ic5xx -ic5xy -ic5xz;
 -ic5xy ic5yy -ic5yz;
 -ic5xz -ic5yz ic5zz];
ic6=[ic6xx -ic6xy -ic6xz;
 -ic6xy ic6yy -ic6yz;
 -ic6xz -ic6yz ic6zz];
 % 这里提前写好线性分离形式的惯量，牛顿欧拉计算的时候用不到;
 ii1 = ic1+m1*(Pc111'*Pc111*eye(3)-Pc111*Pc111');
 ii2 = ic2+m2*(Pc222'*Pc222*eye(3)-Pc222*Pc222');
 ii3 = ic3+m3*(Pc333'*Pc333*eye(3)-Pc333*Pc333');
 ii4 = ic4+m4*(Pc444'*Pc444*eye(3)-Pc444*Pc444');
 ii5 = ic5+m5*(Pc555'*Pc555*eye(3)-Pc555*Pc555');
 ii6 = ic6+m6*(Pc666'*Pc666*eye(3)-Pc666*Pc666');

需要注意的是：上面有很多的global参数，这里可以直接在仿真以及后面的计算力矩的时候来用符号表示。完成上面的生成参数之后，我们再来用牛顿欧拉方程计算力矩.

function tao = gen_6dof_dy_cal_newton_dynamic(q,dq,ddq)
 global g m1 m2 m3 m4 m5 m6;
 global ic1 ic2 ic3 ic4 ic5 ic6;
 global Pc111 Pc222 Pc333 Pc444 Pc555 Pc666;
 global P001 P112 P223 P334 P445 P556 P667;
 qq1 = q(1); qq2 = q(2); qq3 = q(3);
 qq4 = q(4); qq5 = q(5); qq6 = q(6);
 dqq1 = dq(1)*pi/180.0; dqq2 = dq(2)*pi/180.0;
 dqq3 = dq(3)*pi/180.0; dqq4 = dq(4)*pi/180.0;
 dqq5 = dq(5)*pi/180.0; dqq6 = dq(6)*pi/180.0;
 ddqq1 = ddq(1)*pi/180.0; ddqq2 = ddq(2)*pi/180.0;
 ddqq3 = ddq(3)*pi/180.0; ddqq4 = ddq(4)*pi/180.0;
 ddqq5 = ddq(5)*pi/180.0; ddqq6 = ddq(6)*pi/180.0;
 R01 = splitT_R(hrotz(qq1)); R10 = R01';
 R12 = splitT_R(hrotx(-90)*hrotz(qq2-90)); R21 = R12';
 R23 = splitT_R(hrotz(qq3)); R32 = R23';
 R34 = splitT_R(hrotx(-90)*hrotz(qq4)); R43 = R34';
 R45 = splitT_R(hrotx(90)*hrotz(qq5)); R54 = R45';
 R56 = splitT_R(hrotx(-90)*hrotz(qq6)); R65 = R56';
 Z111 = [0 0 1]'; Z222 = [0 0 1]'; Z333 = [0 0 1]'; Z444 = [0 0 1]'; Z555 = [0 0 1]'; Z666 = [0 0 1]'; 
 w000 = [0 0 0]'; dw000 = [0 0 0]'; v000 = [0 0 0]'; dv000 = [0 0 g]';
 %1->6.c
 [w101, dw101 ,dv101 ,dvc101]=cal_single_motion(R10,w000,dw000,dqq1,Z111,ddqq1,P001,dv000,Pc111);
 [Fc101,Nc101] = cal_single_FN(m1,dvc101,ic1,dw101,w101);
 [w202, dw202 ,dv202 ,dvc202]=cal_single_motion(R21,w101,dw101,dqq2,Z222,ddqq2,P112,dv101,Pc222);
 [Fc202,Nc202] = cal_single_FN(m2,dvc202,ic2,dw202,w202);
 [w303, dw303 ,dv303 ,dvc303]=cal_single_motion(R32,w202,dw202,dqq3,Z333,ddqq3,P223,dv202,Pc333);
 [Fc303,Nc303] = cal_single_FN(m3,dvc303,ic3,dw303,w303);
 [w404, dw404 ,dv404 ,dvc404]=cal_single_motion(R43,w303,dw303,dqq4,Z444,ddqq4,P334,dv303,Pc444);
 [Fc404,Nc404] = cal_single_FN(m4,dvc404,ic4,dw404,w404);
  [w505, dw505 ,dv505 ,dvc505]=cal_single_motion(R54,w404,dw404,dqq5,Z555,ddqq5,P445,dv404,Pc555);
 [Fc505,Nc505] = cal_single_FN(m5,dvc505,ic5,dw505,w505);
 [w606, dw606 ,dv606 ,dvc606]=cal_single_motion(R65,w505,dw505,dqq6,Z666,ddqq6,P556,dv505,Pc666);
 [Fc606,Nc606] = cal_single_FN(m6,dvc606,ic6,dw606,w606);
 %6->1
 R67 = eye(3);n707 = [0 0 0]';f707 = [0 0 0]';
 [f606,n606] = cal_single_fn(R67,f707,Fc606,Nc606,n707,Pc666,P667);
 [f505,n505] = cal_single_fn(R56,f606,Fc505,Nc505,n606,Pc555,P556);
 [f404,n404] = cal_single_fn(R45,f505,Fc404,Nc404,n505,Pc444,P445);
 [f303,n303] = cal_single_fn(R34,f404,Fc303,Nc303,n404,Pc333,P334);
 [f202,n202] = cal_single_fn(R23,f303,Fc202,Nc202,n303,Pc222,P223);
 [f101,n101] = cal_single_fn(R12,f202,Fc101,Nc101,n202,Pc111,P112);
 tao(1) = n101(3); tao(2) = n202(3); tao(3) = n303(3); 
 tao(4) = n404(3); tao(5) = n505(3); tao(6) = n606(3);
end
 function [w, dw ,dv ,dvc]=cal_single_motion(R,w0,dw0,dq,Z,ddq,P01,dv0,Pc)
 w = R*w0+dq*Z;
 dw = R*dw0+cross(R*w0,dq*Z)+ddq*Z;
 dv = R*(cross(dw0,P01)+cross(w0,cross(w0,P01))+dv0);
 dvc = cross(dw,Pc)+cross(w,cross(w,Pc))+dv;
end
function [Fc,Nc] = cal_single_FN(m,dvc,ic,dw,w)
 Fc = m*dvc;
 Nc = ic*dw+cross(w,ic*w);
end
function [f,n] = cal_single_fn(R,f1,Fc1,Nc1,n2,Pc,P)
 f = R*f1 + Fc1 ;
 n = Nc1 + R*n2 + cross(Pc,Fc1) +cross (P,R*f1) ;
end

然后再运行仿真，执行仿真模块可以看到如下：

Video_2022-09-22_172433

通过仿真环境中的结果直接导入到matlab的工作空间，然后通过计算两者之间的误差，即可得到牛顿欧拉公式的正确性：

验算程序如下：

format long g;
sum = length(t);
tao1 = linspace(0,0,sum);
tao2 = linspace(0,0,sum);
tao3 = linspace(0,0,sum);
tao4 = linspace(0,0,sum);
tao5 = linspace(0,0,sum);
tao6 = linspace(0,0,sum);
for i = 1:sum 
 q(1) = q1(i,2); q(2) = q2(i,2); q(3) = q3(i,2); q(4) = q4(i,2); q(5) = q5(i,2); q(6) = q6(i,2); 
 dq(1) = dq1(i,2); dq(2) = dq2(i,2); dq(3) = dq3(i,2); dq(4) = dq4(i,2); dq(5) = dq5(i,2); dq(6) = dq6(i,2);
 ddq(1) = ddq1(i,2); ddq(2) = ddq2(i,2); ddq(3) = ddq3(i,2); ddq(4) = ddq4(i,2); ddq(5) = ddq5(i,2); ddq(6) = ddq6(i,2);
% 想用何种方式去求取都是可以的
 tao = gen_6dof_dy_cal_newton_dynamic(q,dq,ddq);%
 % tao = gen_6dof_dy_cal_data_linear_separate(q,dq,ddq);
  %tao = gen_6dof_dy_cal_data_min_param(q,dq,ddq);
 tao1(i) = tao(1); tao2(i) = tao(2); tao3(i) = tao(3); 
 tao4(i) = tao(4); tao5(i) = tao(5); tao6(i) = tao(6);
end
figure;
subplot(6,1,1);
plot(tao1,'r');hold on;plot(tao_data_1.Data,'b');
subplot(6,1,2);
plot(tao2,'r');hold on;plot(tao_data_2.Data,'b');
subplot(6,1,3);
plot(tao3,'r');hold on;plot(tao_data_3.Data,'b');
subplot(6,1,4);
plot(tao4,'r');hold on;plot(tao_data_4.Data,'b');
subplot(6,1,5);
plot(tao5,'r');hold on;plot(tao_data_5.Data,'b');
subplot(6,1,6);
plot(tao6,'r');hold on;plot(tao_data_6.Data,'b');
figure;
% tao_data_1.Data 是simulink所产生的，直接从工作空间中拿过来使用;
subplot(6,1,1);
plot(tao1'-tao_data_1.Data);
subplot(6,1,2);
plot(tao2'-tao_data_2.Data);
subplot(6,1,3);
plot(tao3'-tao_data_3.Data);
subplot(6,1,4);
plot(tao4'-tao_data_4.Data);
subplot(6,1,5);
plot(tao5'-tao_data_5.Data);
subplot(6,1,6);
plot(tao6'-tao_data_6.Data);

仿真结果如下：

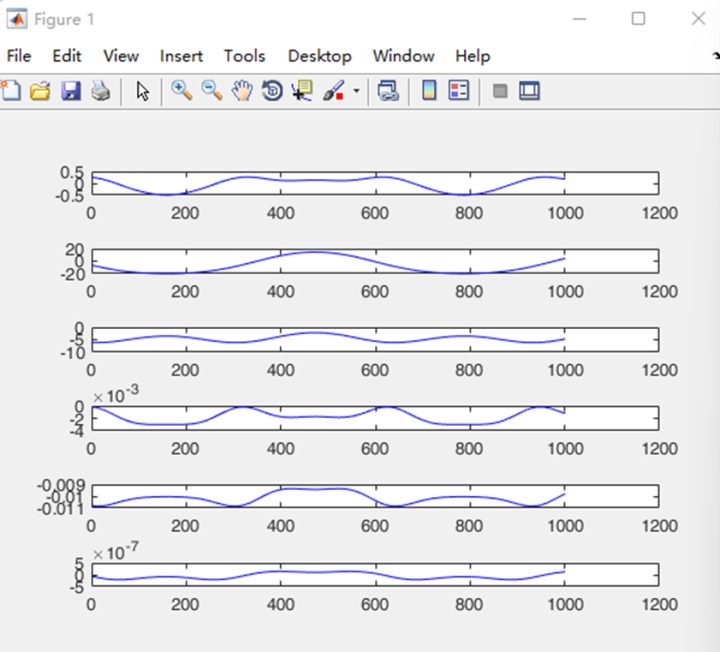
这张图其实有两条线，一条是simulink所生成的曲线，一条为牛顿欧拉公式所求得的力矩曲线，两者已经重合，所以看起来是一条线。

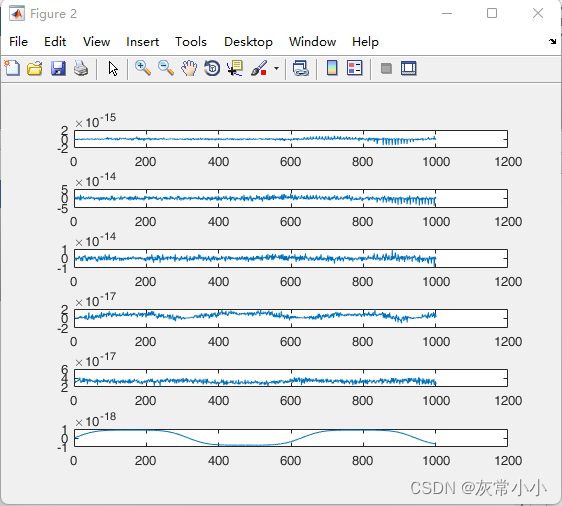
这张图是误差曲线图，也就是仿真结果与牛顿欧拉方程结果相做差得到的结果图。图中的误差只有数值上的误差，没有别的误差，如果误差在10e-10以内，那说明正确，只有在10e-10以外才不会被认为是数值上的误差，可以肯定在某些地方计算不正确。

二、线性分离形式的动力学

在前面写道了关于牛顿欧拉方程得到的动力学仿真模型的正确性，通过平行移轴惯性矩公式可以得出：

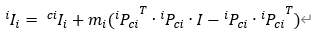
可以将物体质心处的惯量转移到关节处

同时将牛顿欧拉方程的最后修改成

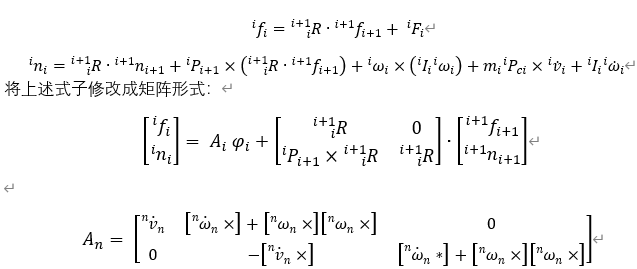
其中

将所有的力矩整合到一起：

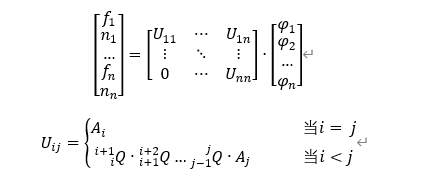
那么就能得到

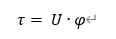
其中

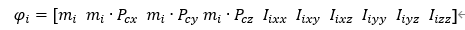
根据上面所述，写得线性分离形式的动力学为：

function tao = gen_6dof_dy_cal_data_linear_separate(q,dq,ddq)
 global g m1 m2 m3 m4 m5 m6;
 global ii1 ii2 ii3 ii4 ii5 ii6 U_r;
 global Pc111 Pc222 Pc333 Pc444 Pc555 Pc666;
 global P001 P112 P223 P334 P445 P556 ;
 Ii11xx = ii1(1,1);Ii11xy = ii1(1,2);Ii11xz = ii1(1,3);
 Ii11yy = ii1(2,2);Ii11yz = ii1(2,3);Ii11zz = ii1(3,3);
 Ii22xx = ii2(1,1);Ii22xy = ii2(1,2);Ii22xz = ii2(1,3);
 Ii22yy = ii2(2,2);Ii22yz = ii2(2,3);Ii22zz = ii2(3,3);
 Ii33xx = ii3(1,1);Ii33xy = ii3(1,2);Ii33xz = ii3(1,3);
 Ii33yy = ii3(2,2);Ii33yz = ii3(2,3);Ii33zz = ii3(3,3);
 Ii44xx = ii4(1,1);Ii44xy = ii4(1,2);Ii44xz = ii4(1,3);
 Ii44yy = ii4(2,2);Ii44yz = ii4(2,3);Ii44zz = ii4(3,3);
 Ii55xx = ii5(1,1);Ii55xy = ii5(1,2);Ii55xz = ii5(1,3);
 Ii55yy = ii5(2,2);Ii55yz = ii5(2,3);Ii55zz = ii5(3,3);
 Ii66xx = ii6(1,1);Ii66xy = ii6(1,2);Ii66xz = ii6(1,3);
 Ii66yy = ii6(2,2);Ii66yz = ii6(2,3);Ii66zz = ii6(3,3);
 fi1 = [m1 m1*Pc111(1) m1*Pc111(2) m1*Pc111(3) Ii11xx Ii11xy Ii11xz Ii11yy Ii11yz Ii11zz]';
 fi2 = [m2 m2*Pc222(1) m2*Pc222(2) m2*Pc222(3) Ii22xx Ii22xy Ii22xz Ii22yy Ii22yz Ii22zz]';
 fi3 = [m3 m3*Pc333(1) m3*Pc333(2) m3*Pc333(3) Ii33xx Ii33xy Ii33xz Ii33yy Ii33yz Ii33zz]';
 fi4 = [m4 m4*Pc444(1) m4*Pc444(2) m4*Pc444(3) Ii44xx Ii44xy Ii44xz Ii44yy Ii44yz Ii44zz]';
 fi5 = [m5 m5*Pc555(1) m5*Pc555(2) m5*Pc555(3) Ii55xx Ii55xy Ii55xz Ii55yy Ii55yz Ii55zz]';
 fi6 = [m6 m6*Pc666(1) m6*Pc666(2) m6*Pc666(3) Ii66xx Ii66xy Ii66xz Ii66yy Ii66yz Ii66zz]';
 fi = [fi1;fi2;fi3;fi4;fi5;fi6];
 qq1 = q(1); qq2 = q(2); qq3 = q(3);
 qq4 = q(4); qq5 = q(5); qq6 = q(6);
 dqq1 = dq(1)*pi/180.0; dqq2 = dq(2)*pi/180.0;
 dqq3 = dq(3)*pi/180.0; dqq4 = dq(4)*pi/180.0;
 dqq5 = dq(5)*pi/180.0; dqq6 = dq(6)*pi/180.0;
 ddqq1 = ddq(1)*pi/180.0; ddqq2 = ddq(2)*pi/180.0;
 ddqq3 = ddq(3)*pi/180.0; ddqq4 = ddq(4)*pi/180.0;
  ddqq5 = ddq(5)*pi/180.0; ddqq6 = ddq(6)*pi/180.0;
 R01 = splitT_R(hrotz(qq1)); R10 = R01';
 R12 = splitT_R(hrotx(-90)*hrotz(qq2-90)); R21 = R12';
 R23 = splitT_R(hrotz(qq3)); R32 = R23';
 R34 = splitT_R(hrotx(-90)*hrotz(qq4)); R43 = R34';
 R45 = splitT_R(hrotx(90)*hrotz(qq5)); R54 = R45';
 R56 = splitT_R(hrotx(-90)*hrotz(qq6)); R65 = R56';
 Z111 = [0 0 1]'; Z222 = [0 0 1]'; Z333 = [0 0 1]'; Z444 = [0 0 1]'; Z555 = [0 0 1]'; Z666 = [0 0 1]'; 
 w000 = [0 0 0]'; dw000 = [0 0 0]'; v000 = [0 0 0]'; dv000 = [0 0 g]';
 [w101, dw101 ,dv101 ,dvc101]=cal_single_motion(R10,w000,dw000,dqq1,Z111,ddqq1,P001,dv000,Pc111);
 [w202, dw202 ,dv202 ,dvc202]=cal_single_motion(R21,w101,dw101,dqq2,Z222,ddqq2,P112,dv101,Pc222);
 [w303, dw303 ,dv303 ,dvc303]=cal_single_motion(R32,w202,dw202,dqq3,Z333,ddqq3,P223,dv202,Pc333);
 [w404, dw404 ,dv404 ,dvc404]=cal_single_motion(R43,w303,dw303,dqq4,Z444,ddqq4,P334,dv303,Pc444);
 [w505, dw505 ,dv505 ,dvc505]=cal_single_motion(R54,w404,dw404,dqq5,Z555,ddqq5,P445,dv404,Pc555);
 [w606, dw606 ,dv606 ,dvc606]=cal_single_motion(R65,w505,dw505,dqq6,Z666,ddqq6,P556,dv505,Pc666);
 A1 = zeros(6,10);A2 = zeros(6,10);A3 = zeros(6,10);A4 = zeros(6,10);A5 = zeros(6,10);A6 = zeros(6,10);
 A1(1:3,1) = dv101;A1(1:3,2:4) = S_alg(dw101)+S_alg(w101)*S_alg(w101);
 A1(4:6,2:4) = -S_alg(dv101);A1(4:6,5:10) = K_alg(dw101)+S_alg(w101)*K_alg(w101);
 A2(1:3,1) = dv202;A2(1:3,2:4) = S_alg(dw202)+S_alg(w202)*S_alg(w202);
 A2(4:6,2:4) = -S_alg(dv202);A2(4:6,5:10) = K_alg(dw202)+S_alg(w202)*K_alg(w202);
 A3(1:3,1) = dv303;A3(1:3,2:4) = S_alg(dw303)+S_alg(w303)*S_alg(w303);
 A3(4:6,2:4) = -S_alg(dv303);A3(4:6,5:10) = K_alg(dw303)+S_alg(w303)*K_alg(w303);
 A4(1:3,1) = dv404;A4(1:3,2:4) = S_alg(dw404)+S_alg(w404)*S_alg(w404);
 A4(4:6,2:4) = -S_alg(dv404);A4(4:6,5:10) = K_alg(dw404)+S_alg(w404)*K_alg(w404);
 A5(1:3,1) = dv505;A5(1:3,2:4) = S_alg(dw505)+S_alg(w505)*S_alg(w505);
 A5(4:6,2:4) = -S_alg(dv505);A5(4:6,5:10) = K_alg(dw505)+S_alg(w505)*K_alg(w505);
 A6(1:3,1) = dv606;A6(1:3,2:4) = S_alg(dw606)+S_alg(w606)*S_alg(w606);
 A6(4:6,2:4) = -S_alg(dv606);A6(4:6,5:10) = K_alg(dw606)+S_alg(w606)*K_alg(w606);
 T12 = [R12 zeros(3,3);S_alg(P112)*R12 R12];
 T23 = [R23 zeros(3,3);S_alg(P223)*R23 R23];
 T34 = [R34 zeros(3,3);S_alg(P334)*R34 R34]; 
 T45 = [R45 zeros(3,3);S_alg(P445)*R45 R45];
 T56 = [R56 zeros(3,3);S_alg(P556)*R56 R56];
 U11 = A1;U12 = T12*A2;U13 = T12*T23*A3;U14 = T12*T23*T34*A4;U15 = T12*T23*T34*T45*A5;U16 = T12*T23*T34*T45*T56*A6;
 U22 = A2;U23 = T23*A3;U24 = T23*T34*A4;U25 = T23*T34*T45*A5;U26 = T23*T34*T45*T56*A6;
 U33 = A3;U34 = T34*A4;U35 = T34*T45*A5;U36 = T34*T45*T56*A6;
 U44 = A4;U45 = T45*A5;U46 = T45*T56*A6;
 U55 = A5;U56 = T56*A6;
 U66 = A6;
 U = [U11 U12 U13 U14 U15 U16;
 zeros(6,10) U22 U23 U24 U25 U26;
 zeros(6,10) zeros(6,10) U33 U34 U35 U36;
 zeros(6,10) zeros(6,10) zeros(6,10) U44 U45 U46;
 zeros(6,10) zeros(6,10) zeros(6,10) zeros(6,10) U55 U56;
 zeros(6,10) zeros(6,10) zeros(6,10) zeros(6,10) zeros(6,10) U66;];
 U_r = [U(6,:);
 U(12,:);
 U(18,:);
 U(24,:);
 U(30,:);
 U(36,:);];
 f = U*fi; 
 tao = U_r*fi;
end

simulink那部分的仿真得出的力矩不需要修改，只需要重新用线性分离形式的力矩做差还是能得到

三、最小集动力学形式

在《机器人动力学与控制》中，作者将基于修改dh模型下，从理论方面验证得到了各个情况下的最小集形式，作者将所有的机械臂类型归结为7大类，如下：

T1:在关节0~关节i-1中存在两个轴向不平行的转动关节；

T2:在关节0~关节i-1中存在转动关节，这些转动关节轴向均平行，但不平行关节i轴向;

T3:在关节0~关节i-1中存在转动关节，且这些转动关节轴向均与关节i轴向平行；

T4:在关节0~关节i-1中无转动关节，亦即关节1~i均为移动关节；

R1:关节0~关节i-1中存在其轴向不与关节i轴向不平行的转动关节；

R2:关节0~关节i-1中不存在其轴向不与关节i轴向平行的转动关节，但存在其轴向不与关节i轴向重合的转动关节或其轴向不与关节i轴向平行的移动关节；

R3:关节0~关节i-1中不存在不与关节i轴向重合的转动关节和其轴向不与关节i轴向平行的移动关节

通用机械臂中，可以得到关节2~关节6均为R1类型，关节1为R3类型：

对于R1跟R3类型的关节，相应的最小参数集如下：

若关节i属于R1，那么连杆i对应的最小惯性参数集为

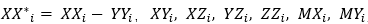
经重组之后连杆i-1的惯性参数为

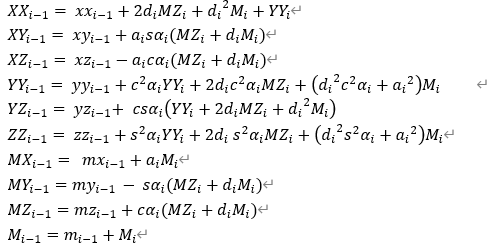
若关节属于R3，那么连杆i-1对应的最小惯性参数集为zz_i；经重组之后连杆i-1的惯性参数为：

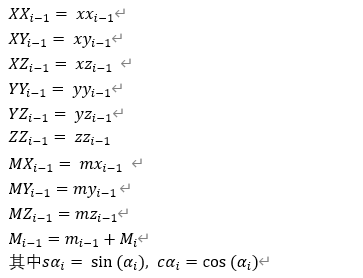
那么根据修改的dh模型表，可以写出各个关节的最小参数集，笔者这里进行单关节的边求取边验证的方式，在前面线性分离的基础上，我们可以先根据dh表，可以求得关节6的最小参数集如下：

%% 尝试写第六关节，其他关节不用动，第六关节力矩计算正确，

 YY6 = Ii66yy;M6 = m6;
 MX6 = m6*Pc666(1); MY6 = m6*Pc666(2);MZ6 = m6*Pc666(3);
 XX6 = Ii66xx-YY6; XY6 = Ii66xy;XZ6 = Ii66xz;YZ6 = Ii66yz;ZZ6 = Ii66zz;
 fi6_min_param = [MX6 MY6 XX6 XY6 XZ6 YZ6 ZZ6]';

结果如下：

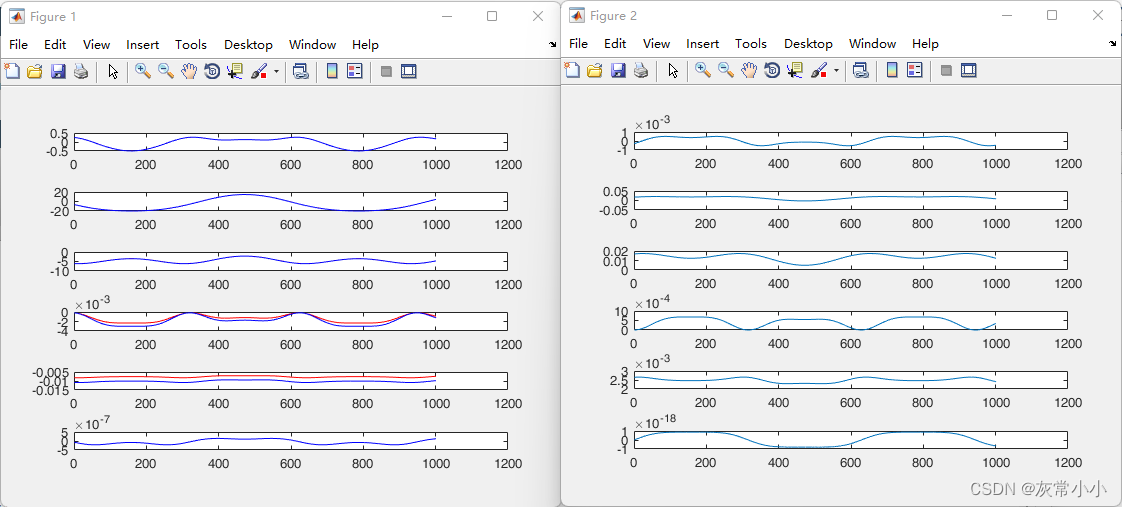
这里可以发现，如果只写第六轴的最小集参数，那么其他轴不正确，只有第六轴只有数值上的误差，其他轴的量级上都不正确。

再写第五轴最小参数集：

YY5 = Ii55yy;M5 = m5+m6;
MX5 = m5*Pc555(1);MY5 = m5*Pc555(2)+(MZ6+d6*M6);MZ5 = m5*Pc555(3); 
 XX5 = Ii55xx-YY5+YY6+2*d6*MZ6+d6^2*M6;XY5 = Ii55xy;
XZ5 = Ii55xz;YZ5 = Ii55yz;
ZZ5 = Ii55zz+YY6+2*d6*MZ6+d6^2*M6;
fi5_min_param = [MX5 MY5 XX5 XY5 XZ5 YZ5 ZZ5]';

结果如下：

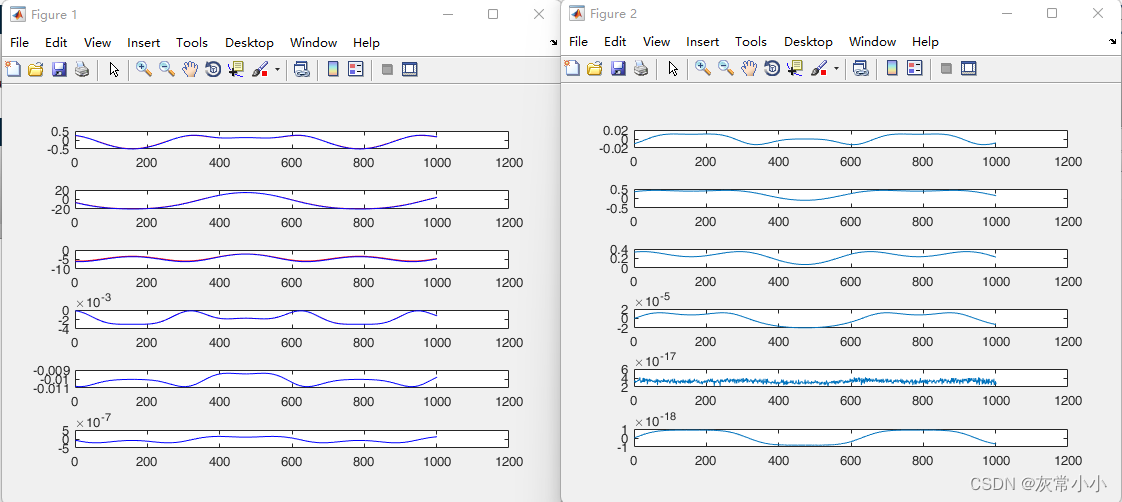
发现同样的五轴六轴的力矩计算正确，其他轴不正确。

依次写出第四轴：

YY4 = Ii44yy;M4 = m4+m5+m6;
 MX4 = m4*Pc444(1);MY4 = m4*Pc444(2)-MZ5;MZ4 = m4*Pc444(3);
 XX4 = Ii44xx-YY4+YY5;XY4 = Ii44xy;XZ4 = Ii44xz;YZ4 = Ii55yz;ZZ4 = Ii44zz+YY5;

在笔者写到第三轴时，发现实际的第三轴最小集参数：

YY3 = Ii33yy;M3 = m3+M4;
 MX3 = m3*Pc333(1)+a4*M4;MY3 = m3*Pc333(2)+(MZ4+d4*M4);MZ3 = m3*Pc333(3);
 XX3 = Ii33xx-YY3+YY4+2*d4*MZ4+(-a4^2+d4^2)*M4;XY3 = Ii33xy-a4*(MZ4+d4*M4);XZ3 = Ii33xz;YZ3 = Ii33yz;ZZ3 = Ii33zz+YY4+2*d4*MZ4+(d4^2+a4^2)*M4;
 XX3 = Ii33xx-YY3+d4^2*M4;XY3 = Ii33xy;XZ3 = Ii33xz-a4*(MZ4-d4*M4);YZ3 = Ii33yz;ZZ3 = Ii33zz+a4^2*M4;

这里的第三轴参数与《机器人动力学与控制》一书中根据书上所写的最小集参数不一样，上面的最小集参数是笔者根据矩阵与实际数据比对而成的。从仿真得到的数据验算来看，上面的最小集参数是正确的，笔者暂时在书上没找到相关错误，如果有朋友能知道为什么书上的地方错了，可以联系笔者。

第二轴：

YY2 = Ii22yy;M2 = m2+m3+m4+m5+m6;
 MX2 = m2*Pc222(1)+a3*M3;MY2 = m2*Pc222(2);MZ2 = m2*Pc222(3);%+MZ3;
 XX2 = Ii22xx-YY2+(-a3^2)*M3; XY2 = Ii22xy;XZ2 = Ii22xz-a3*(MZ3+d3*M3);YZ2 = Ii22yz;ZZ2 = Ii22zz+a3^2*M3;

这里最终的最小集参数也跟书上对不起来，包括一轴

ZZ1 = Ii11zz+YY2+a2^2*M2+YY3+2*d3*MZ3+(a3^2+d3^2)*M3

全部写完之后，验证结果的正确：

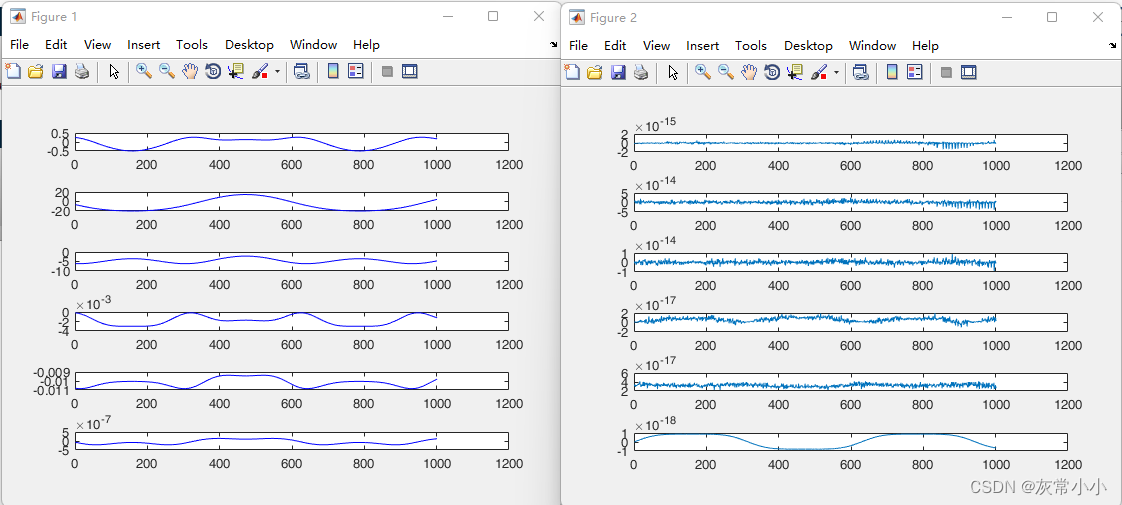
上述所有的结果都是笔者通过仿真与实验得到的。也验证了最小参数集的正确性。

如果上述有什么错误，还请大家见谅，如果有志同道合的朋友想了解这块也可以联系笔者

tiny_h@163.com