一.圆周率
(圆的周长与直径的比值)
圆周率(Pi)是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。π也等于圆形之面积与半径平方之比。是精确计算圆周长、圆面积、球体积等几何形状的关键值。 在分析学里,π可以严格地定义为满足sin x = 0的最小正实数x。圆周率用希腊字母 π(读作pài)表示,是一个常数(约等于3.141592654),是代表圆周长和直径的比值。它是一个无理数,即无限不循环小数。在日常生活中,通常都用3.14代表圆周率去进行近似计算。而用十位小数3.141592654便足以应付一般计算。即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位。
1965年,英国数学家约翰·沃利斯(John Wallis)出版了一本数学专著,其中他推导出一个公式,发现圆周率等于无穷个分数相乘的积。2015年,罗切斯特大学的科学家们在氢原子能级的量子力学计算中发现了圆周率相同的公式 。2019年3月14日,谷歌宣布圆周率现已到小数点后31.4万亿位。
二.蒙特卡洛(Monte Carlo)方法简介
蒙特卡洛是一个地名,位于赌城摩纳哥,象征概率。蒙特卡洛(Monte Carlo)方法是由大名鼎鼎的数学家冯·诺伊曼提出的,诞生于上世纪40年代美国的“曼哈顿计划”。原理是通过大量随机样本,去了解一个系统,进而得到所要计算的值。
*计算圆周率π的原理
一个正方形内部相切一个圆,圆和正方形的面积之比是π/4。
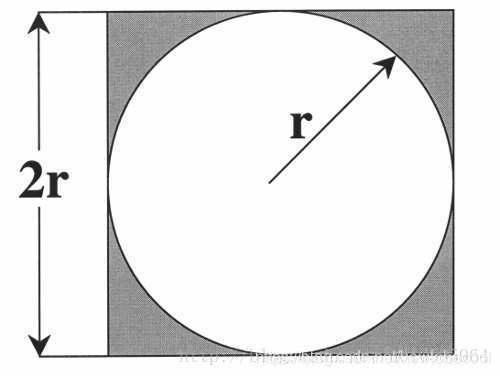
在这个正方形内部,随机产生n个点(这些点服从均匀分布),计算它们与中心点的距离是否大于圆的半径,以此判断是否落在圆的内部。统计圆内的点数,与n的比值乘以4,就是π的值。理论上,n越大,计算的π值越准。





 本文介绍了利用Python通过蒙特卡洛方法计算圆周率,并展示了具体代码和运行结果。圆周率(π)是数学常数,表示圆周长与直径的比例,通常用3.14来近似。文章详细解释了如何借助随机点落在正方形内与圆的关系,通过增加点的数量逐步逼近π的精确值。
本文介绍了利用Python通过蒙特卡洛方法计算圆周率,并展示了具体代码和运行结果。圆周率(π)是数学常数,表示圆周长与直径的比例,通常用3.14来近似。文章详细解释了如何借助随机点落在正方形内与圆的关系,通过增加点的数量逐步逼近π的精确值。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 150
150

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








