二进制数表示形式：原码、反码与补码_用二进制反码和补码运算求-52-20-优快云博客

本文链接：https://blog.youkuaiyun.com/howard2005/article/details/122905462

本文详细介绍了二进制数的计算，包括加法、减法、乘法和除法的运算法则，并探讨了二进制逻辑运算如“与”、“或”、“非”和“异或”。此外，文章阐述了二进制数的表示形式，如原码、反码和补码，以及它们在计算机中的应用。着重讨论了计算机如何通过补码进行负数运算，以及二进制数与十进制数的转换。最后，文章提到了计算机能力的局限性和表数范围，以及符号二进制数转换为十进制数的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、二进制数计算

二进制数在计算机中是应用最广的，因为它最简单，数码仅1和0两个，可以代表电平的高和低，或者电压的正和负，或者电路的开与关等。对于二进制数，除了与十进制数一样可以进行四则算术运算外，还可以进行逻辑运算，因为它只有两个数码，可以代表两种截然相反的状态。

（一）二进制四则运算

二进制数的加、减、乘、除四则算术运算法则其实与十进制数的四则算术运算法则是一一对应的。理解了十进制数的四则算术运算法则，二进制数的四则算术运算就一点都不难了。

1、加法运算法则

$0 + 0 = 0 ， 0 + 1 = 1 ， 1 + 0 = 1 ， 1 + 1 = 10$ ，也就是当两个相加的二进制位仅一位为1时，相加的结果为1；如果两个二进制位全是0，相加的结果仍为0；而如果两个相加的二进制位均为1，则结果为10（相当于十进制中的2），也就是“逢2进1”规则，与十进制中的“逢10进1”的道理一样。
在进行二进制加减法运算时，最关键的一点就是逢2进1，进1当1，而借1当2。大家联想一下我们经常使用的十进制数加法运算法则，那就是逢10进1，进1当1，而借1当10，这样一来我们就好理解了。二进制数的加法运算法则只是把原来十进制数加法运算法则中的10改成了2。
计算 $10010)_2+(11010)_2$ 的过程如下图所示（注意两数要从最低位开始对齐）
1）首先是进行最低位相加，这里加数和被加数都为“0”，根据加法法则可以知道，相加后为“0”；
2）再进行倒数第二位相加，这里加数和被加数都为“1”，根据加法法则可以知道，相加后为“(10)2
”，此时把后面的“0”留下，而把第一位的“1”向高一位进“1”；
3）再进行倒数第三位相加，这里加数和被加数都为“0”，根据加法法则可以知道，本来结果应为“0”，但倒第二位已向这位进“1”了，此时就要同时把“被加数”、“加数”和“进位”这三个数加起来了，所以结果应为0+0+1=1；
4）再进行倒数第四位的相加，这里加数和被加数分别为“1”和“0”，倒数第三位也没有进位，根据加法法则可以知道，相加后为“1”；
5）最后是最高位相加，这里加数和被加数都为“1”，根据加法法则可以知道，相加后为“(10)2
”。同样需把第一位的“0”留下，并向高位进1，这样会产生新的最高位，值为“1”（如果超出了字长的限制，则新产生的最高位将溢出）。
这样 $10010)_2+(11010)_2$ 的最后运算结果为 $101100)_2$ 。

2、减法运算法则

$1 - 1 = 0 ， 1 - 0 = 1 ， 0 - 0 = 0 ， 0 - 1 = - 1$ ，也就是当两个相加的二进制位中同为0或1时，相减的结果为0；如果被减数的二进制位为1，而减数的二进制位为0，则相减的结果仍为1；而如果被减数的二进制位为0，而减数的二进制位为1，则需要向高位借1，但此时是借1当2，与十进制中的借1当10道理一样。
计算 $111010)_2-(101011)_2$ 的过程如下图所示（注意两数要从最低位开始对齐）
1）首先是最低位相减，这里被减数为“0”，减数为“1”，不能直接相减，需要向高位（此时为倒数第二位）借“1”，这样相当于得到了十进制中的“2”，用2减1结果就得到1。
2）再对倒数第二位相减，此时本来被减数和减数均为“1”，但是被减数的该位被上一步借走了1，所以最后就变为“0”（1-1）了。此时也不能直接与减数相减了，又需要向高位（此时为倒数第三位）借1。同样是借1当2，相当于该位总共为0+2=2。这样倒数第二位相减后的结果为2-1=1。
3）用上一步同样的方法计算倒数第三位和倒数第四位的减法运算，结果都为1。
4）再计算倒数第五位的减法运算，此时被减数原来为“1”，可是已被倒数第四位借走了1，所以成了“0”（1-1），而此时减数也为“0”，可以直接相减，得到的结果为“0”。
5）最后计算最高位的相减，被减数和减数均为“1”，可以直接相减，得到的结果为“0”。
这样一来， $111010)_2-(101011)_2$ 的结果是 $001111)_2$ ，由于整数的前导0可以不写，所以最后结果就是 $1111)_2$ 。

3、乘法运算法则

$0 \times 0 = 0 ， 0 \times 1 = 0 ， 1 \times 0 = 0 ， 1 \times 1 = 1$ ，也就只有当两个相乘的二进制位都为1，相乘的结果才为1；两个相乘的二进制位中只要有一位为0（也包括是两位同时为0），则相乘的结果都为0。也可以这么理解：1与任何数相乘的结果就是对应的被乘数；而0与任何数相乘的结果都为0。这与十进制中的乘法运算法则也是一样的。要注意的是，在乘法运算中，乘数的每一位要与被乘数的每一位分别相乘，而不仅是对应位相乘，而且乘数的每一位与被乘数的每一位相乘的结果的最低位要与对应的乘数位对齐。当然这与十进制的乘法运算法则也是一样的，很好理解。
计算 $1010)_2×(101)_2$ 的过程如下图所示（注意两数要从最低位开始对齐）
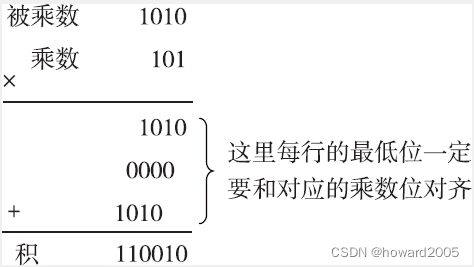
1）首先是乘数的最低位与被乘数的所有位相乘，因为乘数的最低位为“1”，根据乘法法则可以得出，结果其实就是被乘数本身，直接复制下来即可。此处结果就为1010。
2）接着进行的是乘数的倒数第二位与被乘数的所有位相乘，因为乘数的这一位为“0”，根据乘法运算法则可以得出，结果均为“0”。此处结果就为0000。
3）然后是乘数的最高位与被乘数的所有位相乘，此时乘数为“1”，结果就是被乘数本身。此处结果就为1010。
4）最后再按照前面介绍的二进制加法原则对以上三步所得的结果按位相加（但这里的位对齐方式与单纯的二进制数相加不一样，最低位一定要与对应乘数位对齐。这也与十进制的乘法运算方法一样），结果得到 $110010)_2$ 。

4、除法运算法则

当被除数大于除数时，商是“1”；当被除数小于除数时，不够除，商只能是“0”，这与十进制的除法也类似。二进制只有两个数（0，1），因此它的商也只能是1或0。
计算 $11001)_2÷(101)_2$ 的过程如下图所示。
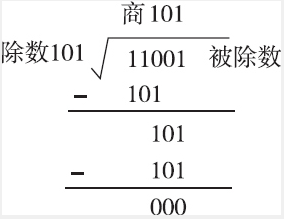
1）因为除数为“101”，有3位，所以在被除数中也至少要取3位（从最高位开始取）。被除数的高3位为“110”，恰好比除数“101”大，可以直接相除，但商只能是1（因为二进制的最大数元就是1），然后把被除数减法商“1”与除数相乘后的结果，得到的值为“1”。
2）再从被除数中取下一位“0”下来，与上一步的差“1”值组成新的被除数，为“10”，显然它比除数“101”小，不够除。于是在商的对应位置上输入“0”。
3）继续从被除数中取下一位“1”下来，与上一步的余数“10”值组成新的被除数，为“101”，此数正好与除数“101”相等，所以此时的商取“1”，正好除尽。
这样一来 $11001)_2÷(101)_2$ 所得的商就是 $101)_2$ 了。

（二）二进制逻辑运算

逻辑运算是指对因果关系进行分析的一种运算，这也是在计算机中经常采用的一种二进制运算。逻辑运算的结果并不表示数值大小，而是表示一种逻辑概念，若成立则为“真”，或用“1”表示；若不成立，则为“假”，或用“0”表示。二进制的逻辑运算主要有“与”、“或”、“非”和“异或”四种。

1、“与”运算（AND）

“与”运算又称逻辑乘，用符号“·”或“∧”来表示。运算法则如下： $0 \land 0 = 0, 0 \land 1 = 0, 1 \land 0 = 0, 1 \land 1 = 1$ ，归纳起来也就是在“与”运算中，只要两个参加“与”运算的数的对应位有一个为0，运算结果就为0；仅当两数的对应位均为1时结果才为1，很容易判断。这与前面介绍的二进制乘法运算是一样的。图1-15所示是两个“与”的逻辑运算示例。下图所示的是两个位数不一样的二进制数进行“与”运算，这时要求两个数从最低位开始对齐，在位数少的二进制的最高位前面加上“0”补齐，使得它与位数多的二进制数有一样的位数。

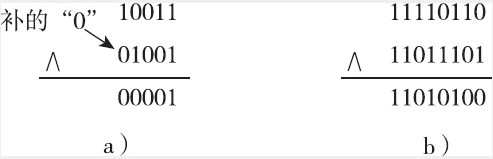
2、“或”运算（OR）

“或”运算又称逻辑加，用符号“+”或“∨”表示。运算法则如下： $0 \lor 0 = 0, 0 \lor 1 = 1, 1 \lor 0 = 1, 1 \lor 1 = 1$ ，也就是说，在“或”运算中，只要两个参加“或”运算数的对应位中有一个为1，运算结果就为1，仅当两数的对应位均为0时结果才为0，也很容易判断。如下图所示是两个“或”的逻辑运算示例。同样，进行“或”运算时要求两数从最低位开始对齐，位数少的数在最高位前面加“0”补齐，最终使两个二进制数的位数相同。

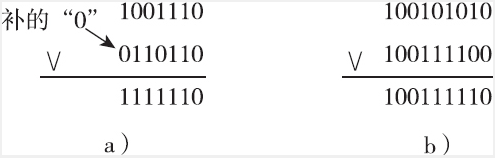
3、“非”运算（NOT）

“非”运算就是逐位求反的运算，其运算法则为：“0”的反值为“1”，“1”的反值为“0”，也就是“0”与“1”互为反。注意：“非运算”只是针对一个二进制数进行的，这与前面的“与”和“或”运算不一样。如“101110101”进行“非”运算后就得到“010001010”（可简写为“10001010”）。

4、“异或”运算（XOR）

“异或”运算用符号“⊕”来表示。其运算法则如下： $0 \oplus 0 = 0 ， 0 \oplus 1 = 1 ， 1 \oplus 0 = 1 ， 1 \oplus 1 = 0$ ，也就是说，当两个参加“异或”运算的二进制数对应位相同时运算结果为0，不同时运算结果为1。下图所示是“异或”逻辑运算示例。同样，进行“异或”运算时要求两数从最低位开始对齐，位数少的数在最高位前面加“0”补齐，最终使两个二进制数的位数相同。

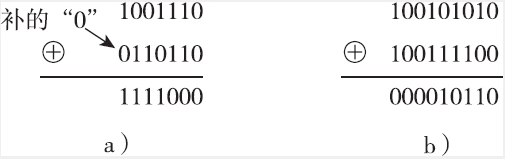
二、二进制数的表示

原码、反码、补码和移码。其实它们都是计算机中二进制数（称之为“机器数”）的不同表示形式，之所以会有这么多码，最根本的原因就是计算机只有加法运算器，减法运算需要转换成负数的加法。这里又出现一个问题，那就是计算机如何来识别负数？因为它不能像人的大脑一样可以识别“+”、“-”之类的符号，故必须用一个专门的位来表示数的符号，这就是计算机中的“有符号数”的由来。计算机中所有数据最终都是使用二进制数表示的。如何将一个负数用二进制形式来表示？其实，在计算机中负数是以其正数的补码形式表示的。

（一）真值和字长

负数是通过其正数的补码形式来表示的，那什么是补码呢？这还得从原码、反码说起。在计算机二进制数中其实也包括符号位，并不是所有位都代表数据本身，就像我们常用的十进制数中有正、有负一样。但是二进制中没有“-”这个符号，那么计算机中的机器数的符号是怎样规定的呢？这得从机器数的两个基本概念（真值和字长）说起。

1、真值

计算机中的二进制机器数分为“有符号数”和“无符号数”两种。“无符号数”就是二进制数的每一位都代表对应位的数值；而在“有符号数”中规定最高位用来表示数据符号，其中1代表负，0代表正，这样一来机器数本身就不等于真正的数值了。例如有符号数10000101，其最高位1代表负，所以余下的“0000101”才是数值本身，所以其真正数值是-5，而如果是无符号数，则10000101所代表的是133。为区别起见，把带符号位的机器数所对应的真正数值称为机器数的“真值”。例：00100001的真值=0 0100001=+33（正号可以不写，可以直接写成33），10100011的真值=1 0100011=-35。

2、字长

在机器数中还有一个概念需要首先弄明白，那就是“字长”。“字长”是指计算机一次可处理的二进制数的码位长度，是计算机进行数据存储和数据处理的运算单位。如我们通常所指的32位处理器，就是指该处理器的字长为32位，也就是一次能处理32位二进制数。通常称16位是一个字，32位是一个双字，64位是两个双字。
数值的转换结果是与字长有关的。如果计算机字长为8位，十进制中的数+5转换成二进制就是00000101，-5转换成二进制就是10000101；但如果字长是16位，+5转换的结果就是00000000 00000101，而-5转换成二进制就是1000000000000101了。也就是对应的机器数要转换为字长所代表的位数。
字长越长代表计算机的处理能力越强，可以处理的数越大。如现在字长普遍是64位的了，这样一来计算机可以处理的二进制数码位长度最大为64位，去掉符号位，则表示计算机可以处理的最大二进制数为2的63次方，最小二进制数就是-2的63次方。而在8位字长中，因为最高位要用于符号位，所以实际可以处理的数值大小范围为-127~-0~0~127（即 $2^7-1$ ），共256个数了；但如果字长是16位，可以处理的数值大小就可以是-32677~-0~0~32767( $2^{15}-1$ )。
注意：以上的“-0”与“0”的机器数是不一样的，在8位字长中，-0为1 0000000，而+0为0 0000000；在16位字长中，-0为1 0000000 00000000，而+0为0 0000000 00000000。所以在二进制的机器数中，0也有两个（-0和0），且表示形式并不一样。

（二）二进制表示形式

1、原码

（1）概念

最高位为符号位，其余为真值部分
$X]_原=符号位+|绝对值|$

（2）优点

真值和其原码表示之间的对应关系简单，容易理解

（3）缺点

计算机中用原码进行加减运算比较困难
0的表示不唯一

（4）数0的原码

8位数0的原码：

$\colorbox{Yellow}00000000$
$\colorbox{Yellow}10000000$

由此可见，数0的原码不唯一。

2、反码

（1）概念

对一个机器数X：

若 $X > 0$ ，则 $X]_反=[X]_原$
若 $X < 0$ ，则 $X]_反=对应原码的符号位不变，数值部分按位求反$

（2）案例

例1、-52的反码

$X = - 52 = - 0110100$

$[X]_原=\colorbox{yellow}10110100$
$[X]_反=\colorbox{yellow}11001011$

例2、0的反码

$[+0]_反= [+0]_原= \colorbox{yellow}00000000$
$[-0]_原= \colorbox{yellow}10000000$
$[-0]_反 = \colorbox{yellow}11111111$

由此可见，数0的反码也不是唯一的。

3、补码

（1）概念

对于机器数X：

$若X>0，则[X]_补= [X]_反= [X]_原$
$若X<0，则[X]_补= [X]_反+1$

（2）案例

例1、-52的补码

$X = - 52 = - 0110100$

$[X]_原=\colorbox{yellow}10110100$
$[X]_反=\colorbox{yellow}11001011$
$[X]_补= [X]_反+1=\colorbox{yellow}11001100$

例2、0的补码

$[+0]_补= [+0]_原=\colorbox{yellow}00000000$
$[-0]_反+1=\colorbox{yellow}11111111+1 =\colorbox{red}1\colorbox{yellow}00000000=\colorbox{yellow}00000000$
说明：对8位字长，进位（红色1）被舍掉

例3、钟表案例 - 将指针从5点拨到1点

两钟拨法：

逆时钟拨： $5 - 4 = 1$
顺时钟拨： $\colorbox{red}{12} + 1 = 1$ （ $12$ 为模，自动丢失）

对模12，减法变加法

$4]_补=12-4=8$ （ $8$ 为 $- 4$ 的补数）
$5 - 4 = 5 + 8$
$5-4=5+(-4)=5+(12-4)=5+8=\colorbox{red}{12} +1=1$

（3）补码的算术运算

通过引进补码，可将减法运算转换为加法运算。

$X+Y]_补=[X]_补+[Y]_补$
$X-Y]_补=[X+(-Y)]_补 =[X]_补+[-Y]_补$

例1、计算66-51

$66 - 51 = 66 + (- 51) = 15$
用二进制补码运算：

$[+66]_补= [+66]_原= \colorbox{yellow}01000010$
$[-51]_原=\colorbox{yellow}10110011$
$[-51]_补=\colorbox{yellow}11001101$
$[66-51]_补=[+66]补+ [-51]补= \colorbox{red}1\colorbox{yellow}00001111=\colorbox{yellow}00001111=15$

例2、X = -52 = -0110100，Y = 116 = +1110100，求X + Y的值

$[X]_原=\colorbox{yellow}10110100$
$[X]_补= [X]_反+1=\colorbox{yellow}11001100$
$[Y]_补= [Y]_原=\colorbox{yellow}01110100$
$[X+Y]_补= [X]_补+ [Y]_补=\colorbox{yellow}11001100+\colorbox{yellow}01110100=\colorbox{yellow}01000000$
最高位是0，说明是正数，补码等于原码，即符号位+真值

$\therefore X+Y=[X+Y]_补=\colorbox{yellow}01000000=\colorbox{yellow}+1000000=64$

例3、X = 34 = +0100010，Y = -52 = -0110100，求X + Y的值

$[X]_补=[X]_原=\colorbox{yellow}00100010$
$[Y]_原=\colorbox{yellow}10110100$
$[Y]_补=[Y]_反+1=\colorbox{yellow}11001011+1=\colorbox{yellow}11001100$
$[X+Y]_补= [X]_补+ [Y]_补=\colorbox{yellow}00100010+\colorbox{yellow}11001100=\colorbox{yellow}11101110$
最高位是1，说明是负数，补码不等于原码，补码不是符号位+真值

$\therefore X+Y=[[X+Y]_补]_补=[\colorbox{yellow}11101110]_补=[\colorbox{yellow}11101110]_反+1=\colorbox{yellow}10010001+1=\colorbox{yellow}10010010=-18$

（4）编译系统将负数转换成补码

现代计算机系统中，程序设计时，负数可用“-”表示，由编译系统将其转换为补码。
案例演示：若输入数 $= - 3$ ，程序编译后的值 $= F D H$
$X = - 3 = - 0000011$
$[X]_原=\colorbox{yellow}10000011$
$[X]_补=[X]_反+1=\colorbox{yellow}11111100+1=11111101=FDH$

（5）特殊数10000000

对无符号数： $10000000)_B=128$
在原码中定义为： $10000000)_B=-0$
在反码中定义为： $10000000)_B= -127$
在补码中定义为： $10000000)_B= -128$

三、计算机能力的局限性

（一）计算机的运算能力是有限的

计算机无力解决无法设计出算法的问题
无法处理无穷运算或连续变化的信息

（二）计算机能够表示的数（表数）的范围是有限的

计算机的表数范围受字长的限制
对8位机而言
– 无符号数的最大值： $11111111$
– 有符号正数的最大值： $\colorbox{yellow}0111 1111$
当运算结果超出计算机表数范围时，将产生溢出

1、无符号整数的表示范围

当计算机中数的运行结果超出表数范围时，则产生溢出。
无符号整数的表数范围： $0 ≤ X ≤ 2^n-1$ （ $n$ 表示字长）
无符号数加减运算溢出的判断方法：当最高位向更高位有进位（或借位）时则产生溢出。

2、有符号整数的表示范围

（1）原码和反码

$2^{n-1} -1) ≤ X ≤ 2^{n-1} -1$

（2）补码

$2^{n -1}≤ X ≤ 2^{n-1} -1$

（3）对8位二进制数

原码： $- 127 ～ + 127$
反码： - $127 ～ + 127$
补码： $- 128 ～ + 127$

（4）符号数运算中的溢出判断

两个有符号二进制数相加或相减时，若运算结果超出可表达范围，则产生溢出
溢出的判断方法：最高位进位状态 $\bigoplus$ 次高位进位状态＝1，则结果溢出。
例：最高位进位状态与次高位进位状态不同就会溢出
除法运算溢出时，产生"除数为0"中断
乘法运算无溢出问题

四、符号二进制数与十进制的转换

（一）转换方法

求出真值
进行转换

（二）计算机中的符号数默认以补码形式表示

原码=符号位+绝对值
正数的补码=原码=符号位+绝对值
负数的补码≠原码 $\Longrightarrow$ 负数的补码≠符号位+绝对值

（三）补码数转换为十进制数

1、对正数

补码=反码=原码，且原码=符号位+真值 $\Longrightarrow$ 正数补码的数值部分为真值

2、对负数

补码≠反码≠ 原码 $\Longrightarrow$ 负数补码的数值部分≠真值

3、案例演示

（1）补码最高位是0的情况

假设 $[X]_补=\colorbox{yellow}00101110_B$
符号位是0，说明是正数，补码=原码=符号位+真值
因此，真值 $=\colorbox{yellow}+0101110_B \Longrightarrow X=\colorbox{yellow}+101110_B=\colorbox{yellow}+46$

（2）补码最高位是1的情况

假设 $[X]_补=\colorbox{yellow}11010010_B$
符号位是1，说明是负数， $X≠\colorbox{yellow}-1010010_B$
欲求 $X$ 真值，需对 $X]_补$ 再取补
$X=[[X]_补]_补=[\colorbox{yellow}11010010_B]_补=[\colorbox{yellow}11010010_B]_反+1=\colorbox{yellow}10101101_B+1=\colorbox{yellow}10101110_B=\colorbox{yellow}- 0101110_B = \colorbox{yellow}- 46$