Android 一阶和二阶贝塞尔曲线

最新推荐文章于 2021-07-20 01:51:49 发布

原创最新推荐文章于 2021-07-20 01:51:49 发布 · 1.4k 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#Android #贝塞尔曲线

02 AndroidUI 专栏收录该内容

16 篇文章

订阅专栏

本文介绍了贝塞尔曲线，它是应用于二维图形的数学曲线，在计算机图形学中很重要。还给出了一阶和二阶贝塞尔曲线公式，一阶曲线可理解为起始点和终点直线上匀速移动的点，二阶曲线的轨迹基于两个一阶曲线中间点的移动。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

参考：
https://baike.baidu.com/item/%E8%B4%9D%E5%A1%9E%E5%B0%94%E6%9B%B2%E7%BA%BF/1091769?fr=aladdin

1 简介

贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线，在一些比较成熟的位图软件中也有贝塞尔曲线工具，如PhotoShop等。

贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。

2 贝塞尔曲线公式

2.1 一阶贝塞尔曲线(线性公式)

一阶贝塞尔曲线公式如下：

$B(t)=(1-t)P_0 + t P_1 ,t\in[0,1]$

动画演示:
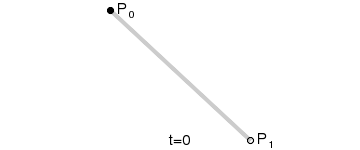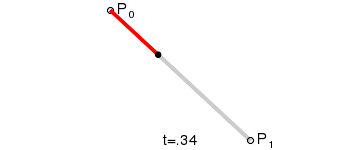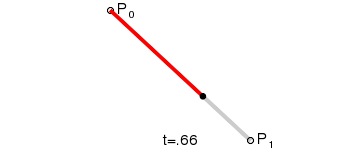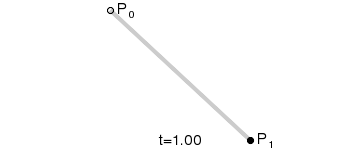
在这里插入图片描述
P0为起点、P1为终点，t表示当前时间，B(t)表示公式的结果值。

注意，曲线的意义就是公式结果B(t)随时间的变化，其取值所形成的轨迹。在动画中，黑色点表示在当前时间t下公式B(t)的取值。而红色的那条线就不在各个时间点下不同取值的B(t)所形成的轨迹。

总而言之：对于一阶贝赛尔曲线，大家可以理解为在起始点和终点形成的这条直线上，匀速移动的点。

2.2 二阶贝塞尔曲线

二阶贝赛尔曲线的公式:

$B(t)=(1-t)^2 P_0 + 2t(1-t)t P_1 + t^2P_2 ,t\in[0,1]$
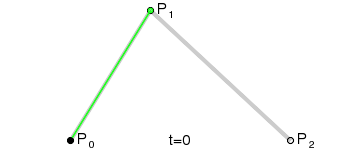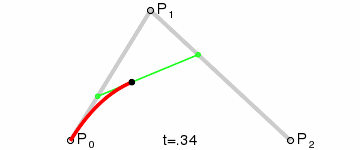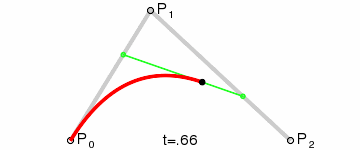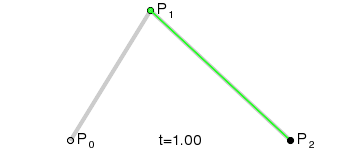
在这里插入图片描述
在这里P0是起始点,P2是终点，P1是控制点。

假设将时间定在t=0.25的时刻，此时的状态如下图所示：
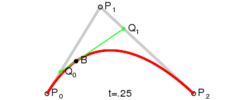
在这里插入图片描述

首先，P0点和P1点形成了一条贝赛尔曲线，还记得我们上面对一阶贝赛尔曲线的总结么：就是一个点在这条直线上做匀速运动；所以P0-P1这条直线上的移动的点就是Q0；

同样，P1,P2形成了一条一阶贝赛尔曲线，在这条一阶贝赛尔曲线上，它们的随时间移动的点是Q1 。最后，动态点Q0和Q1又形成了一条一阶贝赛尔曲线，在它们这条一阶贝赛尔曲线动态移动的点是B 。而B的移动轨迹就是这个二阶贝赛尔曲线的最终形态。从上面的讲解大家也可以知道，之所以叫它二阶贝赛尔曲线是因为，B的移动轨迹是建立在两个一阶贝赛尔曲线的中间点Q0,Q1的基础上的。