文章目录
一. 要点说明
【高等数学】第三章知识点(2)一元函数积分:定积分与反常积分、与几何应用
二. 常见题型
1. 不定积分(见三大积分)
题型一:计算不定积分
题型二:不定积分杂例
2. 定积分
题型一:定积分的概念、性质及几何意义
利用积分中值定理
题型二:定积分的计算
题型三:变上限函数及其应用
积分性质:第一类间断点不影响积分函数的连续性
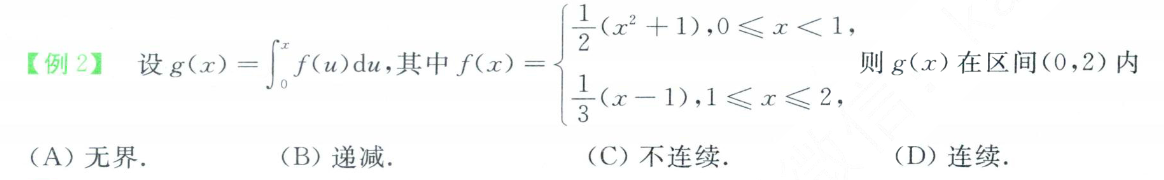
第一个类间断点:积分连续D。

注意原函数要加常数,如果是积分则奇偶会互换。

A,因为有原函数有常数,所以偶不一定变为奇
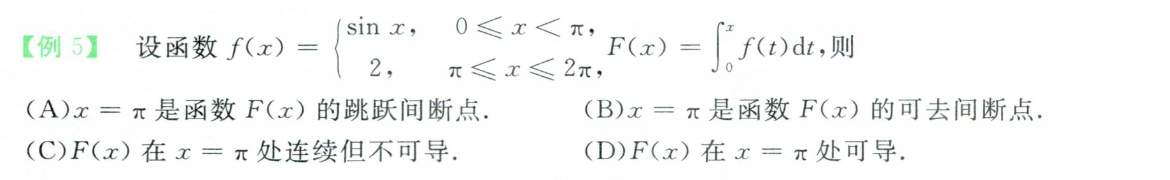
方法一:跳跃间断点,原函数连续但不可导。
方法二:注意:原函数的每一个点是从0开始的累加
带参函数积分:趋近于0时,可以使用中值定理

- 换元:被积函数中不能有积分变量
- 洛必达
- 积分中值定理(趋近于0),或者再洛必达。
类似题目:
简化问题求法

- 求导=0,说明函数是常数
- 进一步:分部积分,令x=0。或者根据性质简单画图,快速得出。
类似题目

简化求法
直接根据sinx图像求解,因为e是递增的。
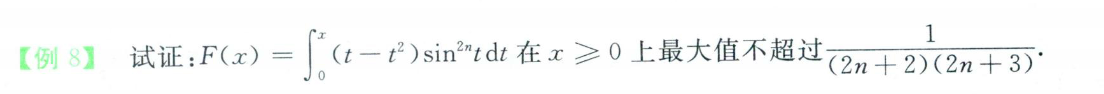
- 求导,求驻点
- 根据驻点找到极值
- 唯一极值点就是最值点。

g(fx)=x

- 求导,求fx的原函数
- f(0)=0,求出C
注意:互为反函数,嵌套=x
先对x或t求导
找到导数与原函数之间的关系,

两个未知参数,其中x跟fx有关,所以t可以随意赋值。
去除绝对值+偶函数积分性质

一. 设x不变,t改变,那正负就好比较了。
- 去绝对值号,得变限函数
- 求两次导:对于积分x作为常数,可以提出来。
二. 一次导=0+二次导符号,唯一极值点,就是最值
**************************求解化简 (利用性质:得出结论:偶函数的积分)”
三. a作为自变量
题型四:积分不等式
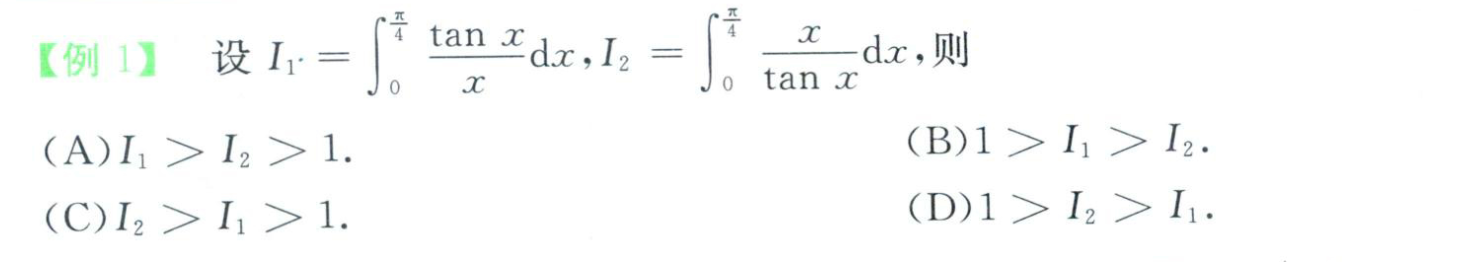
- 在0到π/4 中 tanx大于x。
- 利用积分不等式性质,积分放大,得出和1的关系。
- 不用求解出,采用排除法即可。
类似题:
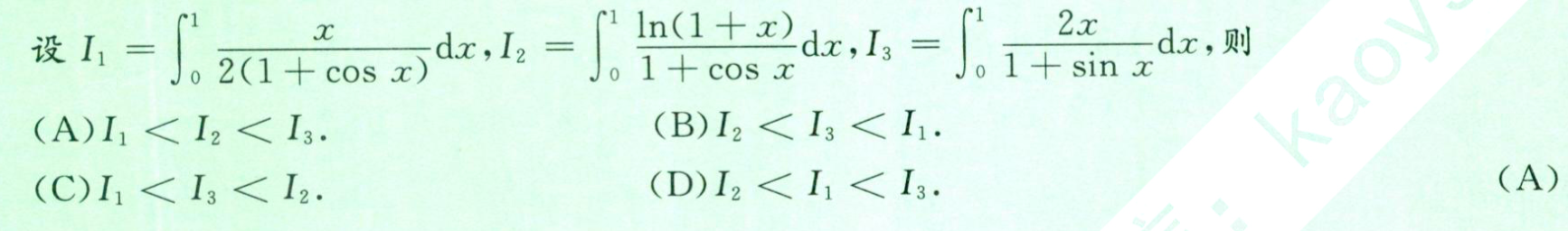
25:对比:找1即可
3. 反常积分
题型一:反常积分的敛散性
25:
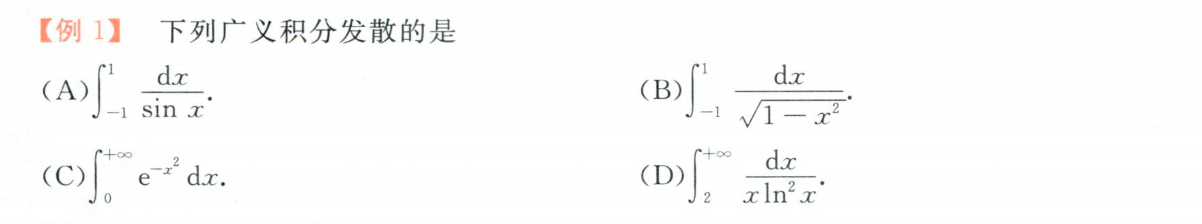
- 有0值:无穷多
- B:原函数:arcsinx
- C:正态分布变式
- D:可积分:凑积分可得
两点:25
- 无定义点:等价无穷小与敛散性

- 敛散性的两个结论:a到b,b到无穷;如果两端的值都是无穷,则分区间,单独判断每端的情况
- 找同敛散性:当趋近于0或无穷时,的等价函数,如果发散则发散
- 利用上述结论

同敛散或更大的敛散
25 分开两段找极限
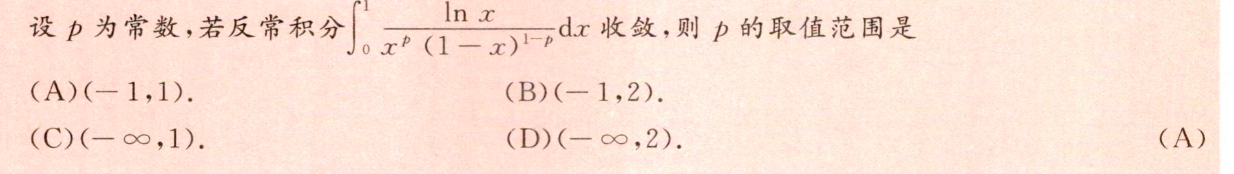

找不出同敛散性的函数,直接积分
4. 定积分的应用(第一道应用大题)
题型一:几何应用
原函数的性质

- 先求原函数:注意积分的累加。
- 原函数再进一步积分
旋转体体积

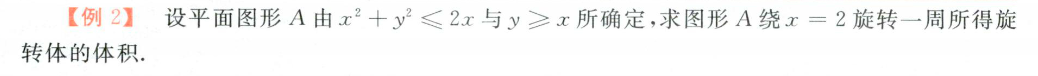
利用二重积分极坐标?

思路和上一样
25

2. 直接是y,不用做替换。被积函数跟面积无关,不用做替换。
3. 直接是x,不用做替换
平面图形的面积

分为直角坐标系、极坐标系,还是二重积分比一重积分要简单。
25

解题思路:
- 说明了是对数螺线:按照极坐标的思路画图像:角度+极坐标。
- 按照习惯规定极轴的方向是水平向右。即x轴。
- 改成二重积分
- 找体积因素(某一点到x轴的周长*面积因素)+二重积分(在这个区域中的积分)
注意和下面的题作对比:利用定积分。什么时候选择定积分、二重积分来求体积。(本题因为是极坐标,所以二重可以)
弧长与侧面积

25

画图:上下左右边界点,描点法
- 重点思路:正常面积积分,分别把ydx,分别带入积分方程,积分区间x转t
- 周长:利用参数的弧长公式
- 面积:正常一元积分,将y、dx以参数方程的形式带入
- 弧长:公式
- 体积:一元积分:找到面积因素,积分
- 侧面积:公式:直角到参数方程的适配过程要熟悉。





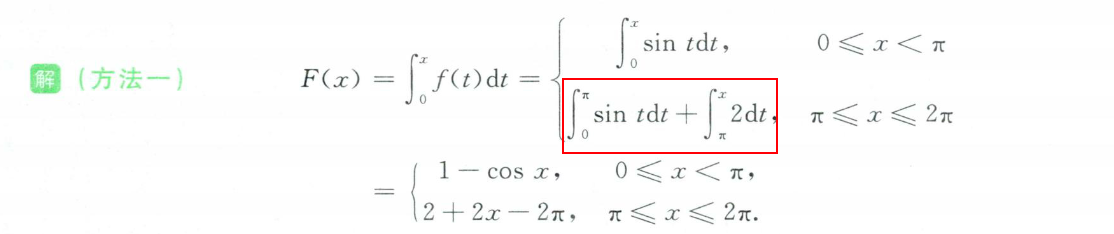
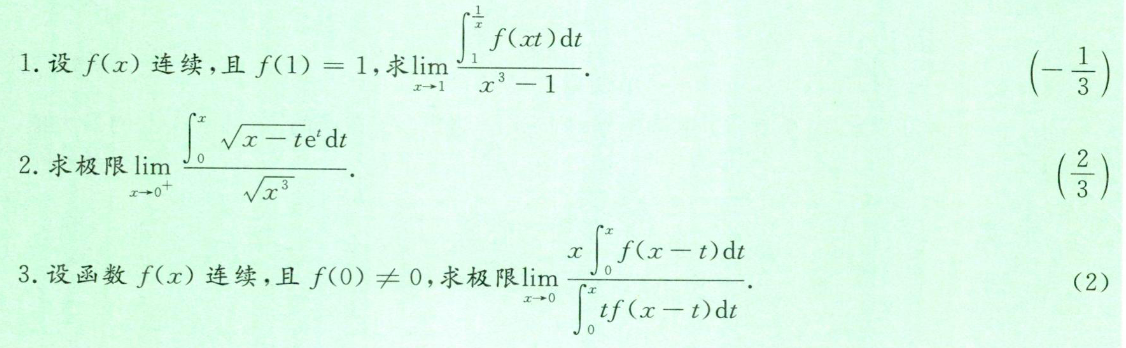


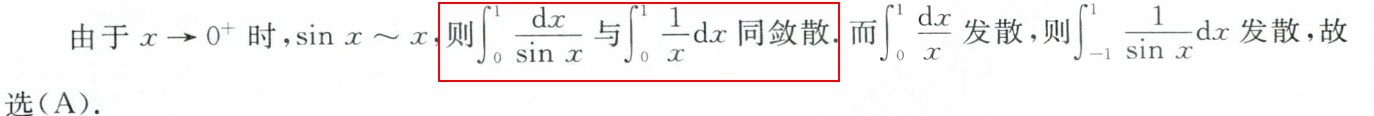


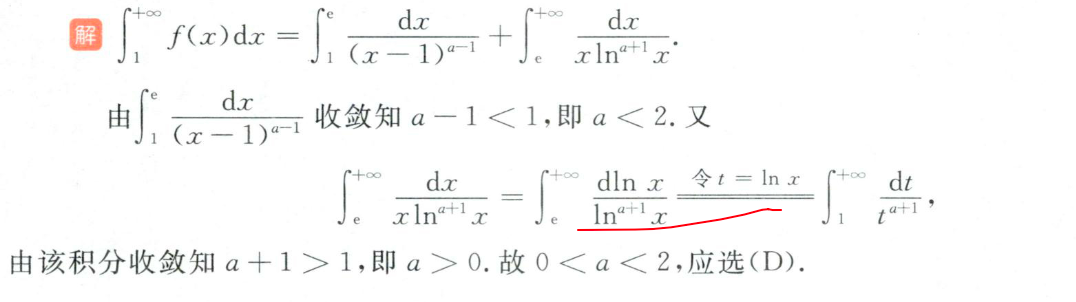
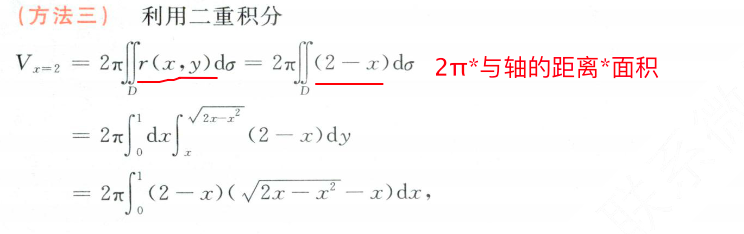
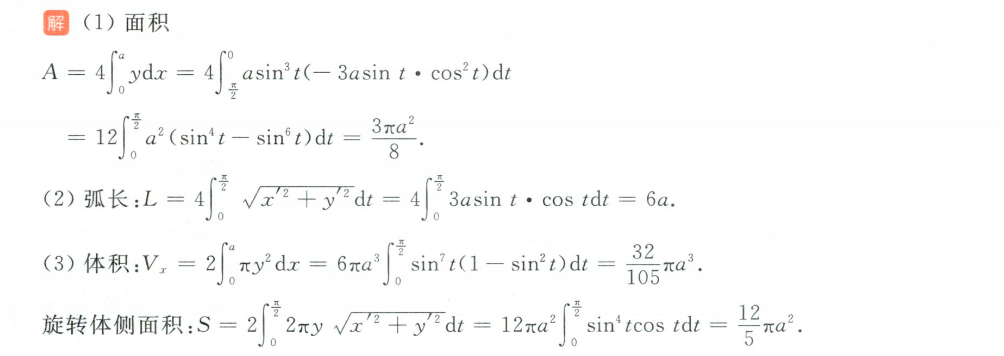


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










