📋 例题一: 理解深度优先搜索树的逻辑
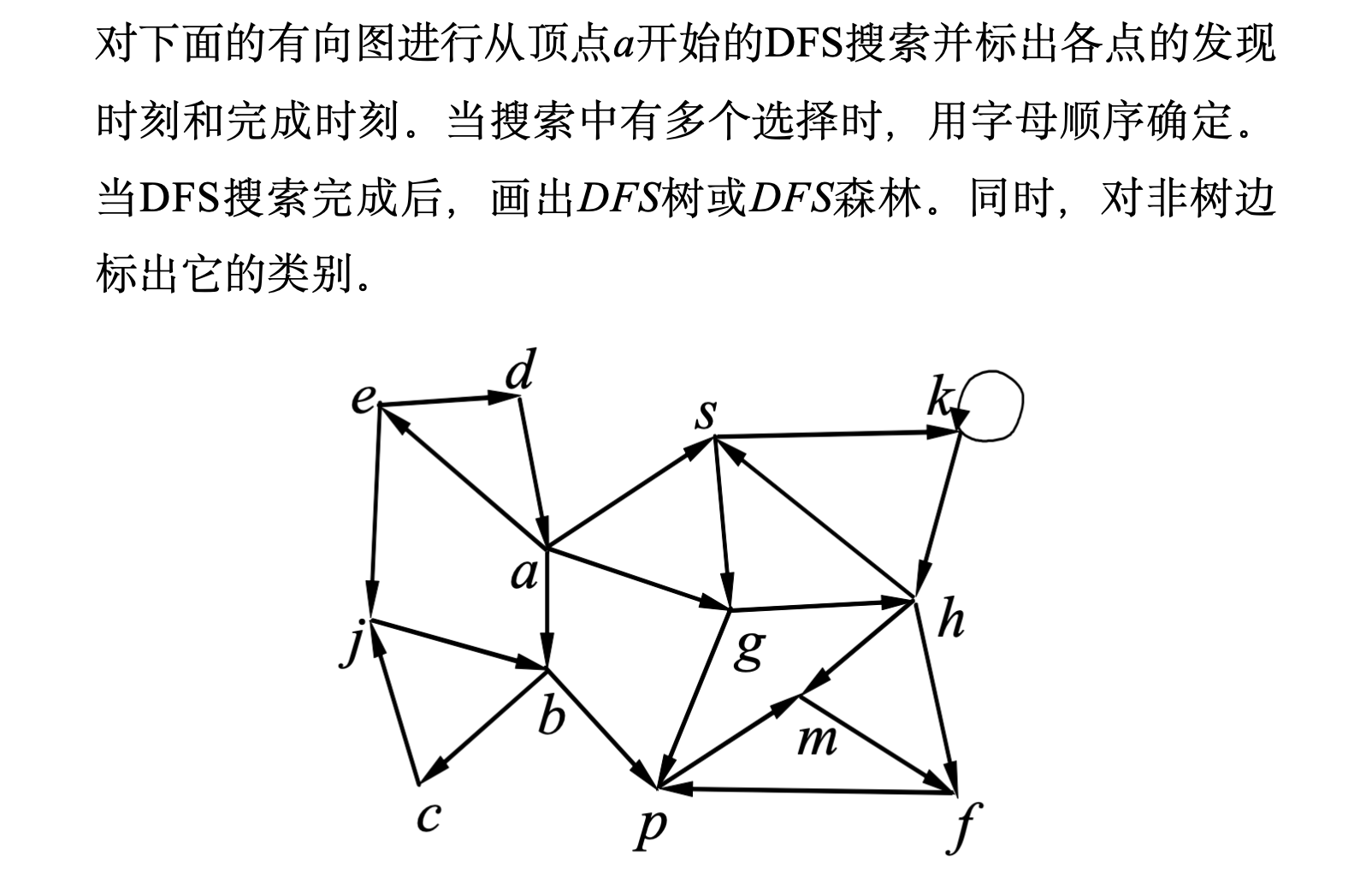
🎯 一、理解"点周游"的逻辑
1.1 什么是"点周游"?
点周游(Vertex Traversal):按照某种顺序系统地访问图中的所有顶点。
DFS的点周游特点:
- 深度优先:选择一条路径,一直走到头
- 回溯:走到头后,返回上一个路口(注意是返回到上一个路口)
- 继续探索:尝试其他未走过的路径
1.2 点周游的执行逻辑
核心思想:像走迷宫一样,一条路走到头,然后回溯。
执行步骤:
1. 选择一个未访问的起点(如 a)
↓
2. 访问这个顶点(标记为 GRAY,记录 d[u])
↓
3. 按顺序访问它的每个未访问邻居
↓
4. 对每个邻居,递归执行步骤2-3(深度优先)
↓
5. 当所有邻居都访问完,标记为完成(标记为 BLACK,记录 f[u])
↓
6. 回溯到父节点
↓
7. 如果还有未访问的顶点,从步骤1开始
关键理解:
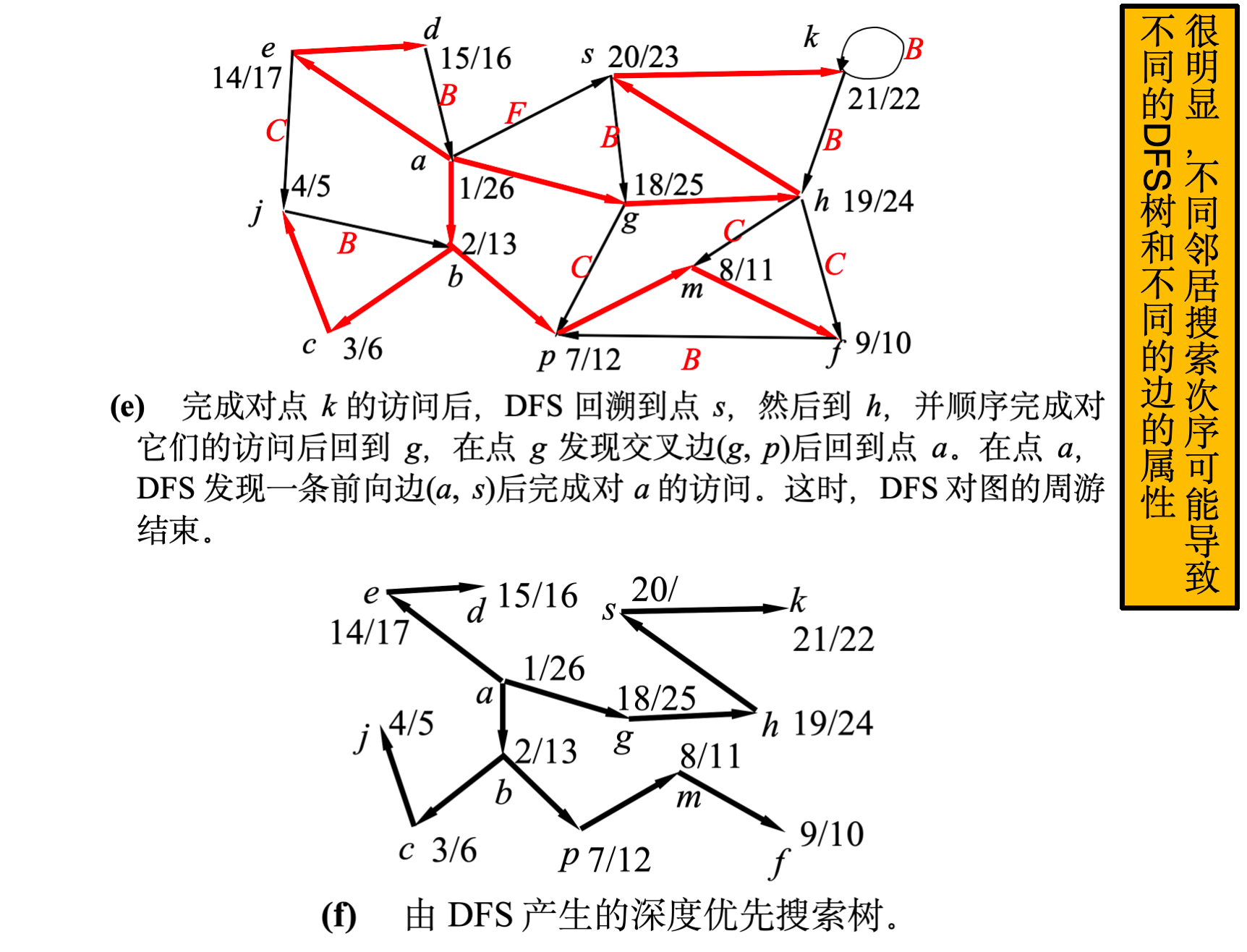
- 深度优先:从 a a a 到 b b b 到 p p p 到 f f f,一条路走到头
- 回溯: f f f 完成后,回到 p p p; p p p 完成后,回到 b b b; b b b 完成后,回到 a a a
- 继续探索:回到 a a a 后,继续访问 a a a 的下一个邻居 g g g
🔄 二、理解"回溯"的逻辑
2.1 什么是"回溯"?
回溯(Backtrack):当从某个顶点出发的所有路径都探索完后,返回到父节点,继续探索父节点的其他路径。
2.2 回溯的触发条件
什么时候回溯?
-
当前顶点没有未访问的邻居
- 例如: f f f 没有出边,立即回溯
-
当前顶点的所有邻居都已访问
- 例如: p p p 的邻居 f f f 已访问完,回溯到 b b b
2.3 回溯的执行过程
回溯的步骤:
当前顶点 u 的所有邻居都访问完
↓
标记 u 为完成(记录 f[u])
↓
u 从 GRAY 变为 BLACK
↓
返回到 u 的父节点 π[u]
↓
父节点继续访问下一个未访问的邻居
关键理解:
- 回溯不是结束:回溯只是返回到父节点,继续探索(记忆)
- 回溯是递归返回:就像函数调用栈,完成当前函数后返回调用者
- 回溯后继续:返回到父节点后,继续访问父节点的其他邻居
✅ 三、理解"顶点标记完成"的逻辑
标记完成的条件:
-
当前顶点没有出边
- 例如: f f f 没有出边,立即标记完成
-
当前顶点的所有邻居都已访问
- 例如: p p p 的邻居 f f f 已访问完,标记 p p p 完成
-
所有邻居都已处理(访问或跳过)
- 例如: b b b 的邻居 p p p 已访问完,标记 b b b 完成
关键理解:
- 完成是递归的:子节点完成后,父节点才能完成
- 完成时间递增: f ( f ) < f ( p ) < f ( b ) f(f) < f(p) < f(b) f(f)<f(p)<f(b)
- 完成意味着回溯:完成一个顶点后,立即回溯到父节点
时间戳的嵌套关系
重要性质:如果 v v v 是 u u u 的儿子,则 [ d ( v ) , f ( v ) ] ⊆ [ d ( u ) , f ( u ) ] [d(v), f(v)] \subseteq [d(u), f(u)] [d(v),f(v)]⊆[d(u),f(u)]
例题验证:
- b b b 是 a a a 的儿子: [ 2 , 13 ] ⊆ [ 1 , 26 ] [2, 13] \subseteq [1, 26] [2,13]⊆[1,26] ✓
- p p p 是 b b b 的儿子: [ 7 , 12 ] ⊆ [ 2 , 13 ] [7, 12] \subseteq [2, 13] [7,12]⊆[2,13] ✓
- f f f 是 p p p 的儿子: [ 9 , 10 ] ⊆ [ 7 , 12 ] [9, 10] \subseteq [7, 12] [9,10]⊆[7,12] ✓
理解:
- 父节点的访问时间区间包含所有子节点的访问时间区间
- 这反映了DFS的递归性质:先完成子节点,再完成父节点(记忆点)
🔙 四、理解"反向边"的逻辑
反向边(Back Edge):从当前顶点 u u u 指向其祖先 v v v 的边。
判断条件:
- 访问边 ( u , v ) (u, v) (u,v) 时, v v v 是 GRAY(灰色)
- v v v 是 u u u 的祖先(在DFS树中, v v v 是 u u u 的上层节点)
反向边的作用:
- 检测环:如果存在反向边,说明图中存在环
- 理解图的结构:反向边揭示了图的循环依赖关系
关键理解:
- GRAY = 正在访问 = 祖先:如果 v v v 是 GRAY,说明 v v v 在调用栈中,是 u u u 的祖先
- 反向边形成环:反向边 ( u , v ) (u, v) (u,v) 说明存在从 v v v 到 u u u 的路径(DFS树路径),加上边 ( u , v ) (u, v) (u,v),形成环
➕ 五、理解"交叉边"的逻辑
交叉边(Cross Edge):从当前顶点 u u u 指向一个既不是其祖先也不是其后代的顶点 v v v 的边。
判断条件:
- 访问边 ( u , v ) (u, v) (u,v) 时, v v v 是 BLACK(黑色)
- 且 d ( v ) < d ( u ) d(v) < d(u) d(v)<d(u)( v v v 比 u u u 更早被发现)
交叉边的特点:
- v v v 已经完成(BLACK)
- v v v 比 u u u 更早被发现
- u u u 和 v v v 不在同一棵子树中
关键理解:
- BLACK + 更早发现 = 交叉边:如果 v v v 是 BLACK 且 d ( v ) < d ( u ) d(v) < d(u) d(v)<d(u),说明 v v v 在另一个分支中, ( u , v ) (u, v) (u,v) 是交叉边
- 交叉边连接不同分支:交叉边连接了DFS树中不同的分支
🔍 六、综合理解:边的分类判断流程
快速判断口诀
白色是树边,灰色是反向,
黑色看时间,前向交叉分。
详细解释:
- WHITE → 树边: v v v 是 u u u 的儿子
- GRAY → 反向边: v v v 是 u u u 的祖先
- BLACK → 看时间戳:
- d ( u ) < d ( v ) d(u) < d(v) d(u)<d(v) → 前向边( v v v 是 u u u 的后代)
- d ( v ) < d ( u ) d(v) < d(u) d(v)<d(u) → 交叉边( u u u 和 v v v 无直系关系)
例题中的边分类总结
树边(Tree Edge):
- ( a , b ) , ( b , p ) , ( p , f ) , ( a , g ) , ( g , h ) , ( h , k ) , ( e , d ) (a, b), (b, p), (p, f), (a, g), (g, h), (h, k), (e, d) (a,b),(b,p),(p,f),(a,g),(g,h),(h,k),(e,d) 等
反向边(Back Edge,标记 B):
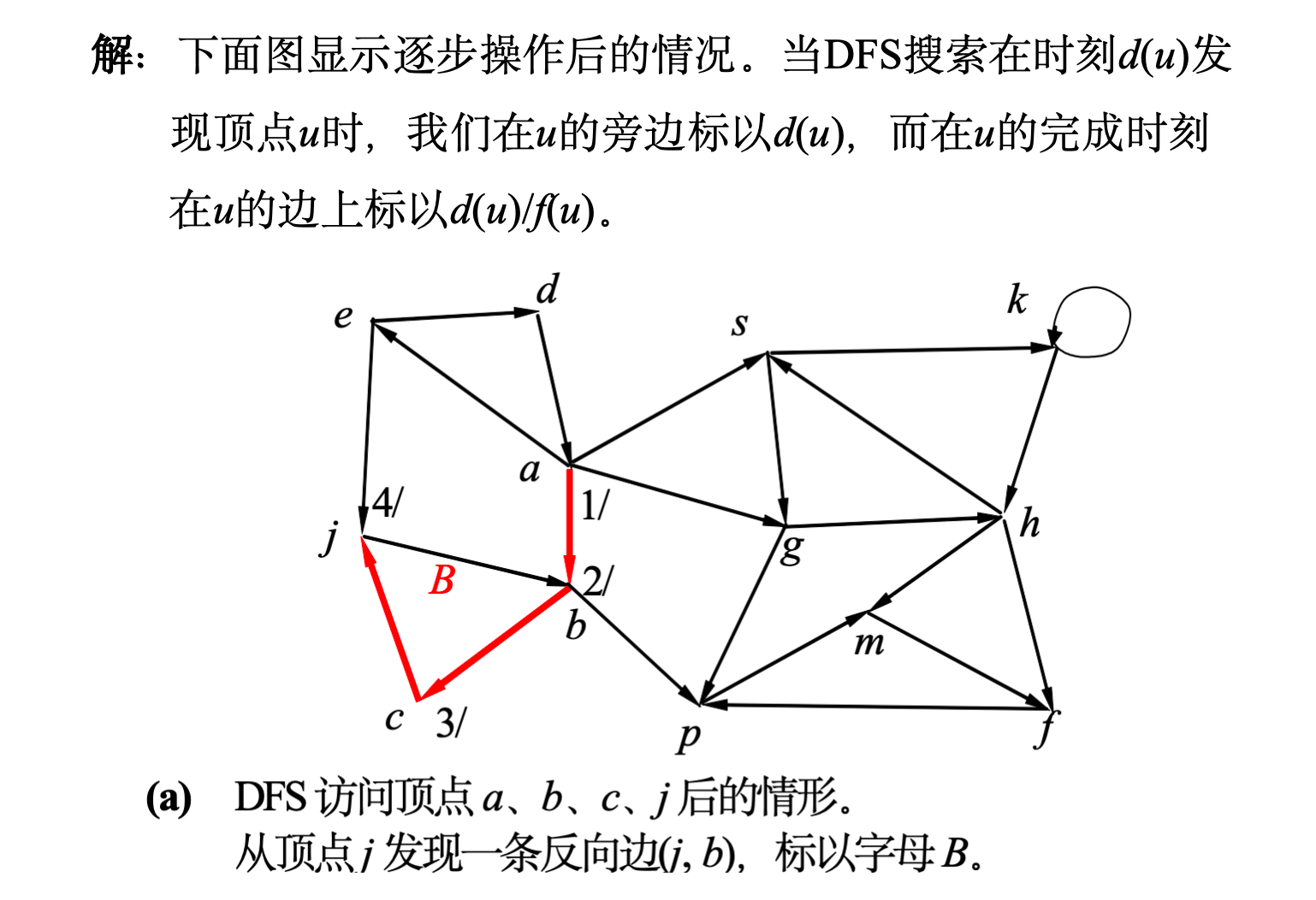
- ( j , b ) (j, b) (j,b): b b b 是 j j j 的祖先
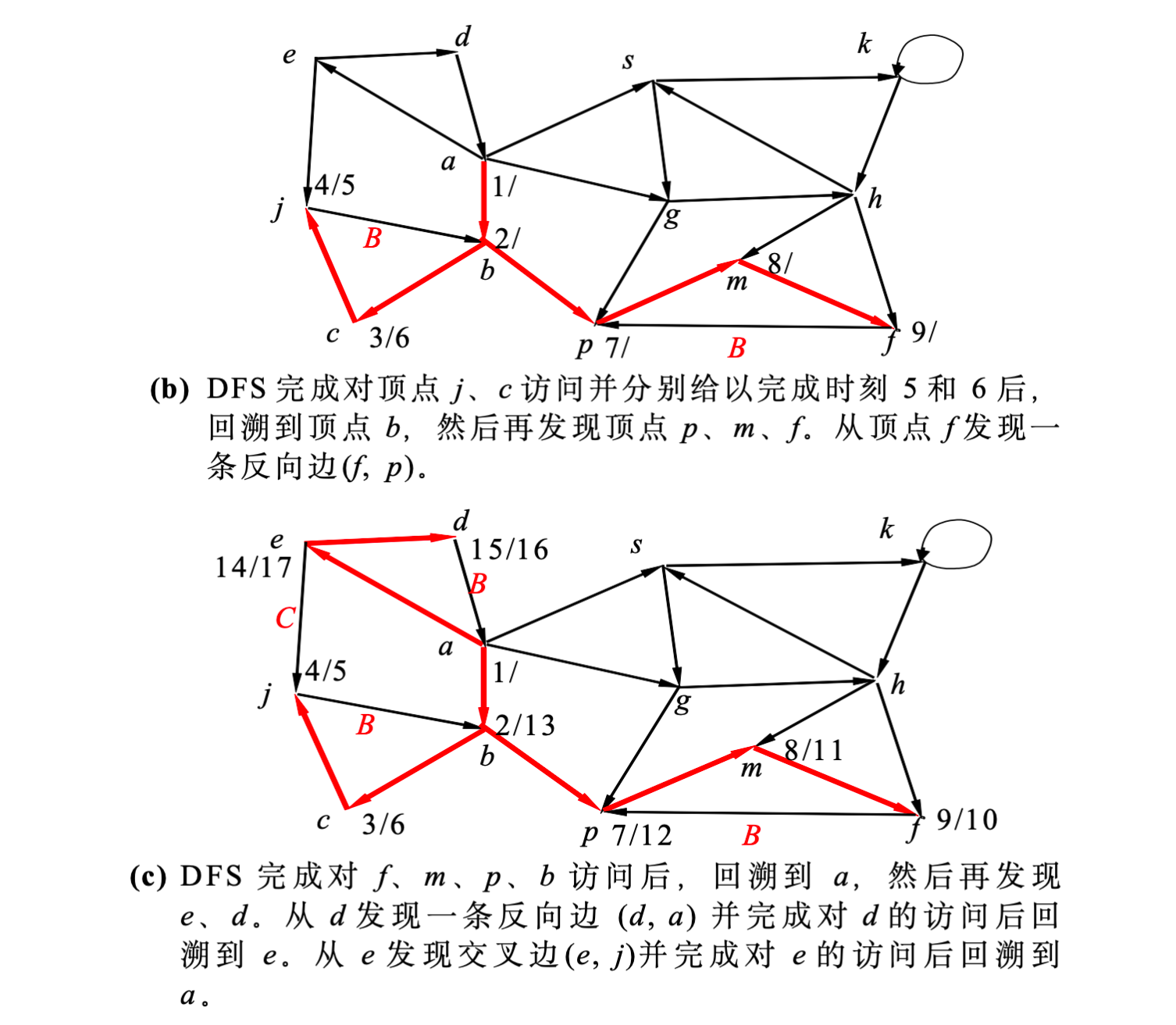
- ( f , p ) (f, p) (f,p): p p p 是 f f f 的祖先
- ( d , a ) (d, a) (d,a): a a a 是 d d d 的祖先
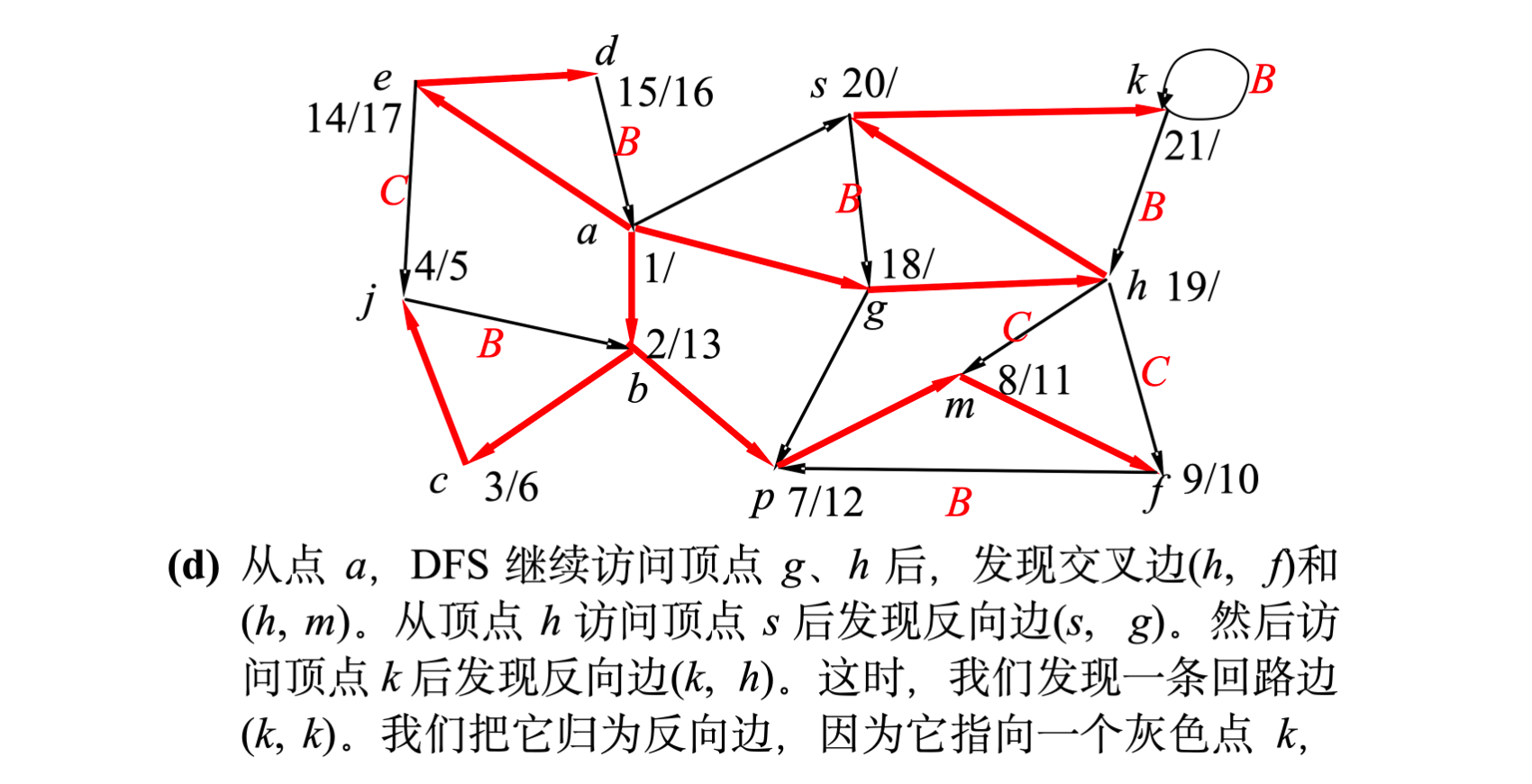
- ( s , g ) (s, g) (s,g): g g g 是 s s s 的祖先
- ( k , h ) (k, h) (k,h): h h h 是 k k k 的祖先
- ( k , k ) (k, k) (k,k):自环,指向自己(GRAY)
前向边(Forward Edge,标记 F):
- ( a , s ) (a, s) (a,s): s s s 是 a a a 的后代,但不在DFS树中(通过其他路径访问)
交叉边(Cross Edge,标记 C):
- ( e , j ) (e, j) (e,j): j j j 是 BLACK, d ( j ) < d ( e ) d(j) < d(e) d(j)<d(e)
- ( h , f ) (h, f) (h,f): f f f 是 BLACK, d ( f ) < d ( h ) d(f) < d(h) d(f)<d(h)
- ( h , m ) (h, m) (h,m): m m m 是 BLACK, d ( m ) < d ( h ) d(m) < d(h) d(m)<d(h)
- ( g , p ) (g, p) (g,p): p p p 是 BLACK, d ( p ) < d ( g ) d(p) < d(g) d(p)<d(g)
📝 总结
核心概念理解:
- 点周游:深度优先探索,回溯继续
- 回溯:子节点完成后,返回父节点
- 完成标记:所有邻居访问完,标记为BLACK
- 反向边:指向祖先(GRAY)的边
- 交叉边:指向已完成且更早发现的顶点(BLACK + d ( v ) < d ( u ) d(v) < d(u) d(v)<d(u))的边
判断流程:
访问边 (u, v)
↓
v 是 WHITE? → 树边
v 是 GRAY? → 反向边
v 是 BLACK? → d(u) < d(v)? → 前向边
→ d(v) < d(u)? → 交叉边
📋 题目二:理解强连通分量
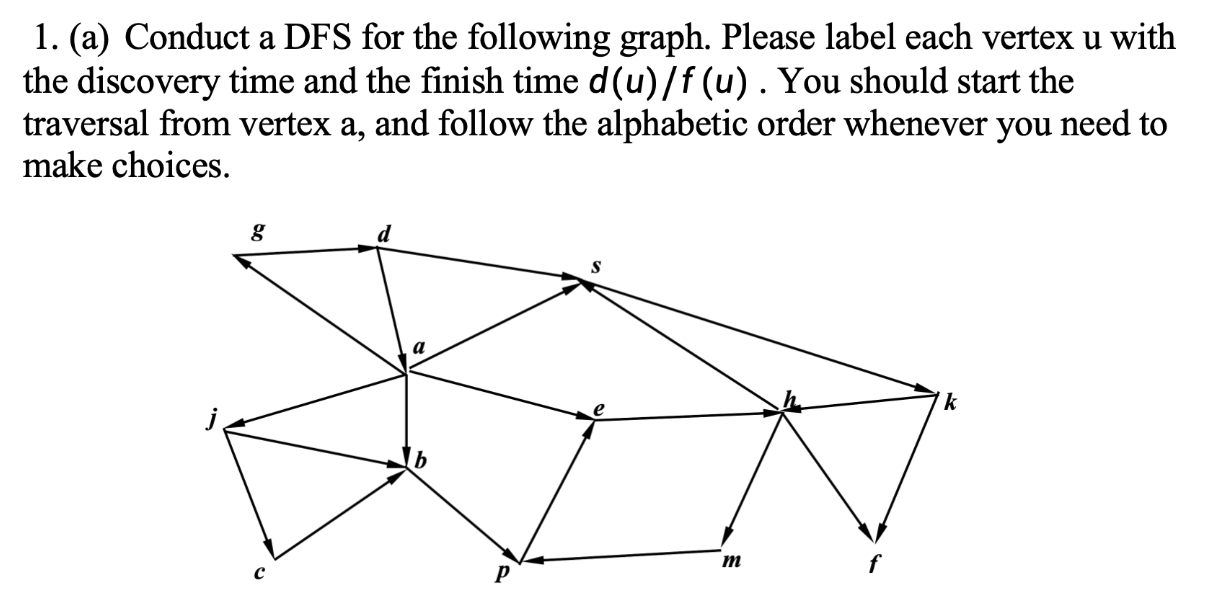
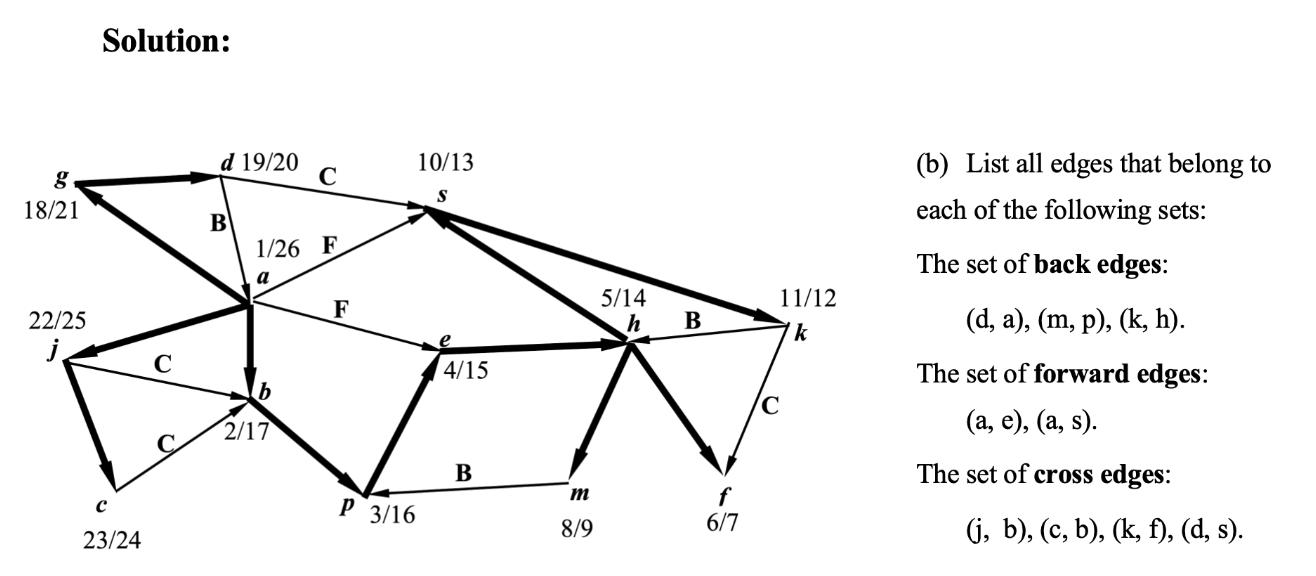
(b) 列出属于以下每个集合的所有边:
- 反向边的集合: (d, a), (m, p), (k, h)
- 前向边的集合: (a, e), (a, s)
- 交叉边的集合:(j, b), (c, b), (k, f), (d, s)
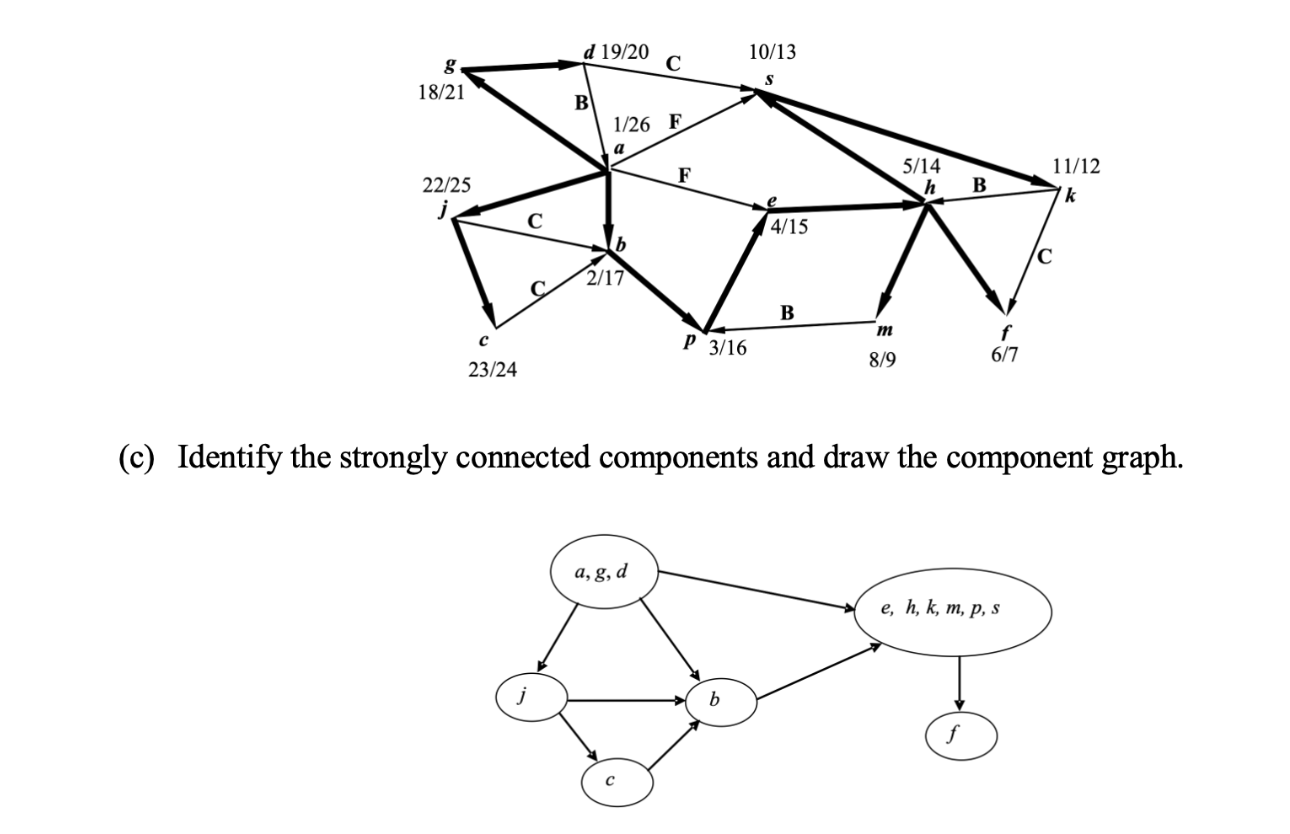
© 找出强连通分量并绘制分量图。
🎯 一、什么是强连通分量?
1.1 强连通的定义
强连通(Strongly Connected):
- 有向图中,如果从顶点 u u u 到 v v v 有路径,且从 v v v 到 u u u 也有路径
- 则称 u u u 和 v v v 是强连通的
关键理解:
- 双向可达:不仅 u u u 能到 v v v, v v v 也能到 u u u
- 有向图特有:无向图中,如果 u u u 能到 v v v,则 v v v 一定能到 u u u(因为边是双向的)
1.2 强连通分量的定义
强连通分量(Strongly Connected Component, SCC):
- 有向图中,任意两个顶点都互相可达的最大顶点集合
- "最大"意味着:不能再加入其他顶点而仍然保持强连通
关键理解:
- 任意两个顶点:分量内的任意两个顶点都互相可达
- 最大:不能再加入其他顶点
- 不相交:不同的强连通分量之间没有公共顶点
✅ 二、验证每个强连通分量
3.1 分量1:{a, g, d}、{e, h, k, m, p, s} (***有交叉点的不算)
验证:任意两个顶点都互相可达
关键理解:
- 这些顶点之间存在循环路径
- 例如:p → e → h → … → p(形成环)
- 任意两个顶点都可以通过这个环互相到达
3.2 分量2:{j}、{b}、{c}、{f}
验证:单个顶点
理解:
- 单个顶点 j j j 自己到自己可达(长度为0的路径)
- 所以 { j } \{j\} {j} 是一个强连通分量
为什么 j j j 不能和其他顶点在一起?
结论:{j} 是一个强连通分量 ✓
🔗 三、理解分量图(Component Graph)
分量图(Component Graph):
- 将每个强连通分量缩成一个顶点
- 如果原图中存在从分量 A A A 到分量 B B B 的边,则在分量图中添加边 A → B A → B A→B
关键性质:
- 有向无环图(DAG):分量图一定是有向无环图
- 拓扑排序:可以对分量图进行拓扑排序
- 简化问题:将复杂的图简化为分量图,更容易分析
理解:
- 分量图将原图"压缩",每个分量变成一个点
- 分量图反映了不同强连通分量之间的关系
- 分量图是DAG,可以进行拓扑排序
💡 四、核心思想与常见模式
核心思想:
- 互相可达:不仅 u u u 能到 v v v, v v v 也能到 u u u
- 形成环:强连通分量内的顶点形成循环路径
- 最大集合:不能再加入其他顶点
常见模式
模式1:单个顶点
- 单个顶点总是自己的强连通分量
模式2:形成环的顶点
- 如果几个顶点形成环(a → b → c → a),则它们在一个强连通分量中
模式3:复杂的循环结构
- 多个顶点通过复杂的路径形成循环,则它们在一个强连通分量中
💡 记忆口诀:强连通分量互相可达,单个顶点也算分量,形成环的顶点在一起,分量图是DAG可排序!
























 1006
1006

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










