一. 导数与微分
1. 内容要点
1.1. 导数与微分的概念
- 导数定义的等价形式
- 左导数、右导数的概念
可微的充要条件:可导
1.2. 导数与微分的几何意义
导数表示斜率、微分表示切线上的增量
1.3. 连续、可导、可微之间的关系:可微与可导之间等价

1.4. 求导公式与求导法则

求导法则
a. 复合函数求导
链式法则
b. 隐函数求导
两种方式
c. 反函数的导数
导数的倒数
d.参数方程

e. 对数求导法
f. 常见高阶导

2. 题型与做题技巧
题型一:导数与微分的概念
1. 利用导数定义求极限

- 凑 1 ∞ 1^∞ 1∞形式,求极限值,带回e,得解。
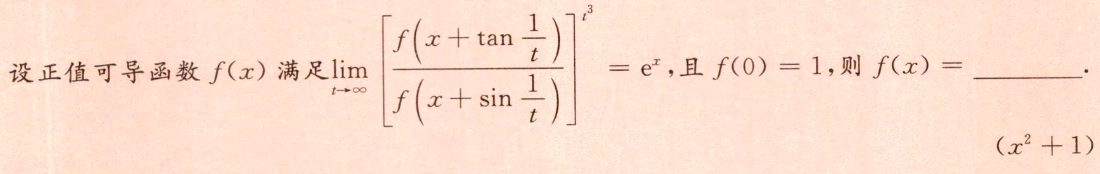

直接洛必达

- 求切点斜率
- 变换式子为无穷小,然后洛必达
2. 利用导数定义求导数
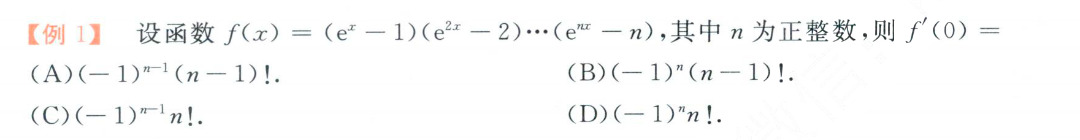
方法1. 利用定义求极限
方法2. 直接求导观察
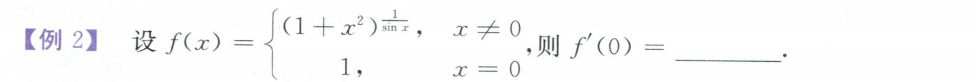
利用导数定义,转换成求极限
注意:分段函数在分界点处一定要用导数定义求。

3. 利用导数定义判断可导性

B:注意连续的条件
D:反例:f=|x|

基于f凑导数形式。

- 学会:拆分并简化问题
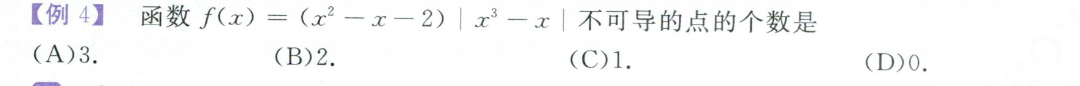
利用导数定义,判断在不同点是否可导。
做题心态:别着急做,要给这道题认真的态度,别跳步。

- 利用导数定义:
利用立方差公式,约掉x-1。

- 直接举一个例子

根据极限的特性,画出fx的图像,不可导点,一目了然

- 按照导数定义
- 按照导数定义+f二阶可导。
题型二:导数的几何意义
方程组(两边对x求导)、参数方程(对t求导,然后除以)的求导法则
极坐标公式求导:(极坐标分别转为y、x,然后参数方程求导)
题型三:导数与微分的计算(见三大计算)
二. 导数应用
1. 内容要点
a. 四大微分中值定理
b. 极值与最值
定义:
因为涉及到领域,极值只能在开区间中取到
极值的必要条件
- 导数=0
- 所有可能的极值点:
- 对于可导函数,所有可能的极值点:驻点
- 对于一般函数,所有可能的极值点:驻点和导数不存在的点
- 判断需要通过充分条件。
极值的三个充分条件
求最值的方法
c. 曲线的曲向与拐点
凹凸性的判断
拐点
定义、必要条件、充分条件
d. 渐进线与曲率
渐近线
平面曲线的曲率
求曲率的公式
2.题型与做题技巧
a. 函数单调性、极值与最值(大题)
例题1: 积分函数求极值

- 求导,找出所有驻点和不可导点
- 看左右导数符号,判断极值。
对于积分函数求导:注意:
- 被积函数中不能含有积分上下限变量,要注意分开。
- 求导时把变量x看成常数。
- 积分上下限本身也要求导。
例题2: 方程组求极值
![]()
- 方程左右两边对x求导,然后令y’的一阶导=0,求出驻点
- 因为判断不出导数变化,所以求二阶导判断。

(保号性)得二阶导>0,一阶导递增,又因为一阶导=0,所以一阶导先小于0,然后再大于0
例题3:抽象方程判断极值

- 思路:极值点,则一阶导=0,分离方程,找到一阶导和二阶导的关系,分析二阶导的正负,进而判断出是极小值还是极大值
- 利用一题:直接求右式极值,判断出正负,进而判断出极值。
b. 曲线的凹向、拐点、渐进线及曲率(大题)

c. 方程根的存在性与个数(大题)












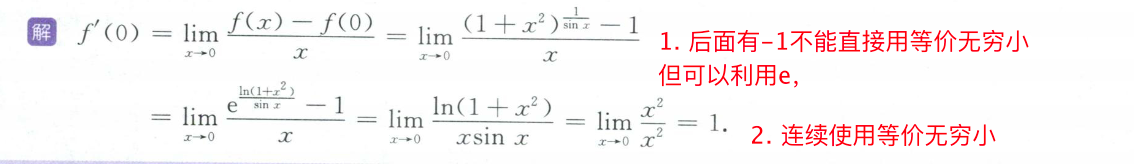


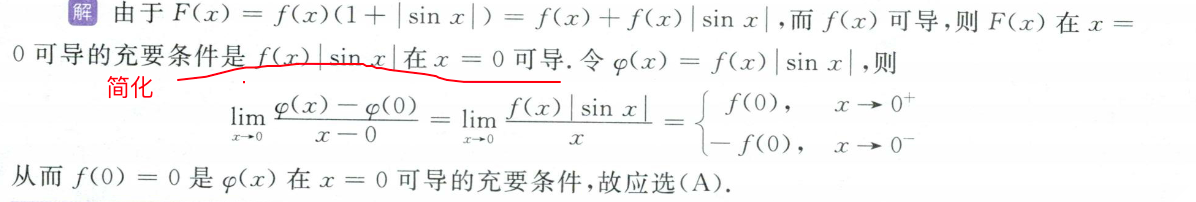


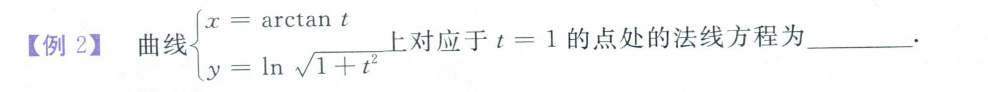
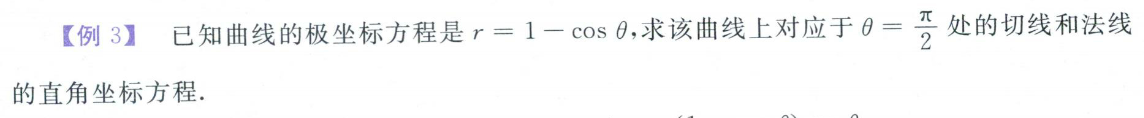



























 1295
1295

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










