【高等数学】【强化第一章】函数极限连续

一. 函数

要点说明

1. 函数奇偶性特性

 

2. 函数周期性特性

 

题型一：复合函数

1. 求复合函数的定义域

1. ing：始终说的是x的取值范围？
   

2. 带入fx反解

 

2. 求复合函数

子函数的定义域分段->子函数值域->找到父函数定义域的函数。

 

题型二： 函数性质

有界性

函数值在定义域左右都存在，即为有界

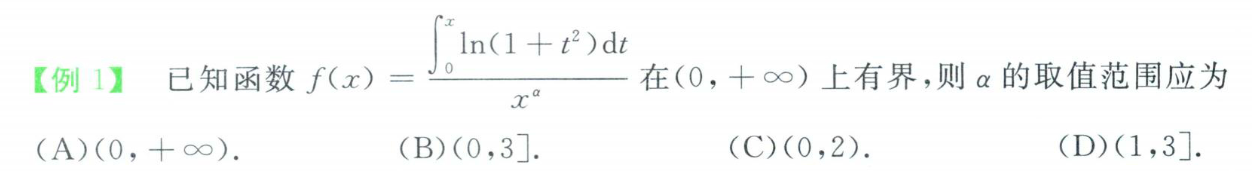
使用洛必达，分析分子、分母谁是高阶。

 

结论：在有限区间内导数有界，则函数有界

 

单调性

A. 0可能是可去间断点，左右导数极限都存在且相等，但是0处不可导
C. 对 （定义）

 

奇偶性

1. 积分对奇偶性的改变

类似例题

 

二. 极限

要点说明

极限定义

数列极限存在：

通常利用此定义求极限，常出现在证明题里。

函数极限：

常见左右极限的情况

注意：0和无穷的极限，都需要考虑正负逼近的逻辑。

 

极限性质

注意：一般保号性，用于判断函数值正负，甚至有时可以判断导数（通过定义）的正负。

 

极限存在定理

 

无穷小

高阶、同阶、等价、无穷小的阶。

 

无穷大

常见无穷大

 

题型一：极限的概念、性质及存在法则

 

极限定义：

注意：充要条件证明的过程，sn->an 记作充分
 

 

例题分析（见三大计算）

 

三. 连续

知识要点

连续的概念：左=右

间断点类型：
第一类间断点：可去、跳跃
第二类间断点：震荡、无穷

函数性质：

零点定理

 

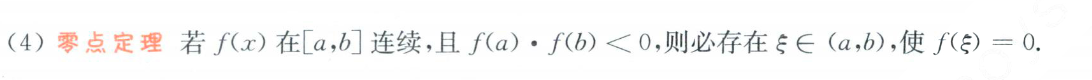
题型一：讨论连续性及间断点类型

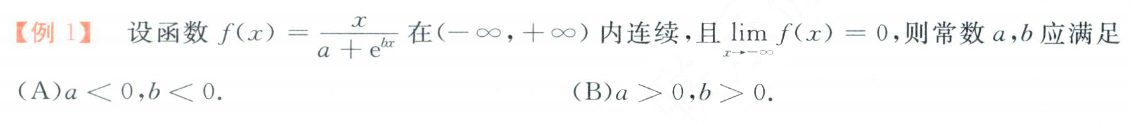
记忆题型

1. b：洛必达，分母无穷大，求出b
2. a：注意别忘了分母不能=0。

 

1. 找到定义不存在的点，然后求左右极限，判断出极限的类型
2. 注意sin(π/2)x=0的情况（周期函数），是无穷间断点。

 

1. 注意要判断父函数和子函数中定义域都不存在的点
2. 其中如果极限等于0，那也是可去间断点

 

1. 所有定义域不存在的点
2. 求极限：利用 $1^{\infty }$ 型进行计算
   

 

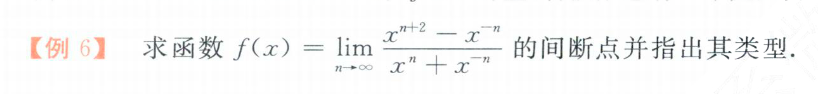
基础题型

 

题型二：介质定理、最值定理及零点定理的证明题（见证明专栏）