【计算机设计与算法-习题2】动态规划应用：矩阵乘法与钢条切割问题

习题一：矩阵链乘法问题——动态规划

⏱️ 预计阅读时间：20-25分钟
🎯 学习目标：掌握如何用动态规划解决矩阵链乘法问题，理解动态规划的两步：计算最优值和记录最优解

---

📖 问题描述：找到最优的矩阵乘法顺序

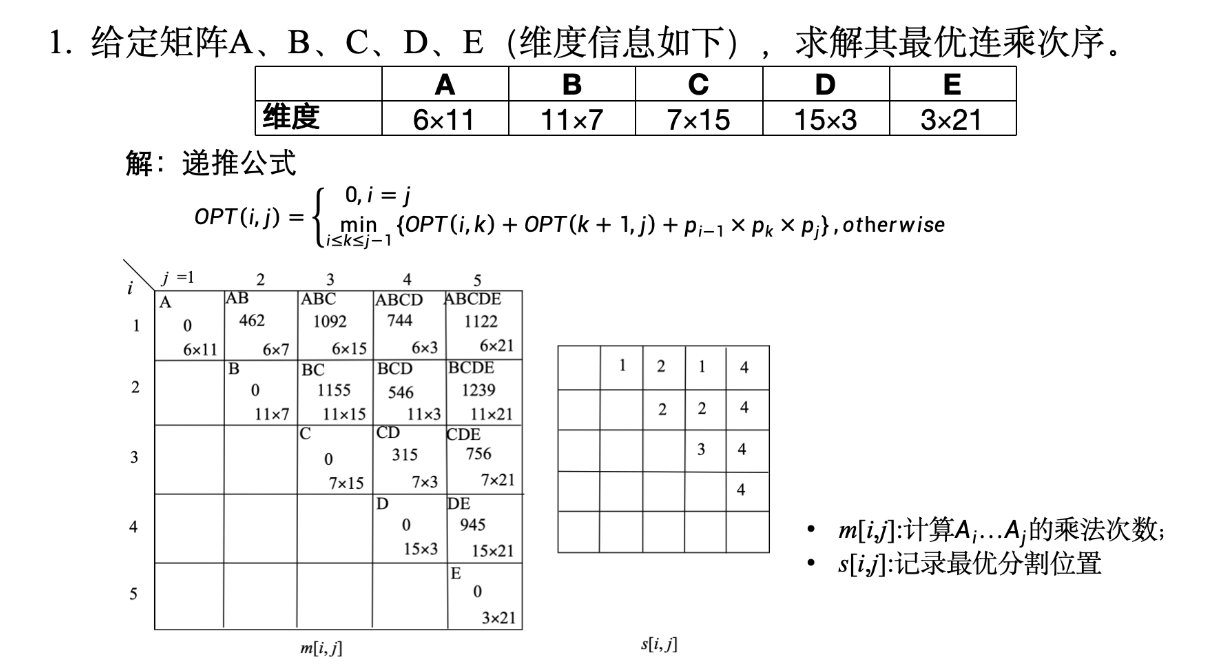
注意：

矩阵连乘分为两部分，首先是根据递推公式计算最小乘法次数，然后需要记录最优分割位置。求解过程需要体现以上两部分

正确思路：动态规划

动态规划的核心思想：将大问题分解为重叠子问题，自底向上求解，避免重复计算。

---

1️⃣ 问题分解的逻辑

核心观察：计算矩阵链 $A_i\times A_{i+1}\times \cdots \times A_j$ 的最优方式，必然在某个位置 $k$ 进行分割。

分解思路：

1. 选择一个分割点 $k$（$i\le k<j$），将矩阵链分成两部分：

   • 左子链：$A_i\times A_{i+1}\times \cdots \times A_k$
   • 右子链：$A_{k+1}\times A_{k+2}\times \cdots \times A_j$

2. 最优子结构性质：

   • 如果整个链的计算方式是最优的，那么左子链和右子链的计算方式也必然是最优的
   • 否则，可以用更优的子链计算方式替换，得到更优的整体方案（矛盾）

3. 总成本分解：
   $$\text{总成本}=\text{左子链成本}+\text{右子链成本}+\text{合并成本}$$

   其中：

   • 左子链成本：计算 $A_i\times \cdots \times A_k$ 的最少乘法次数
   • 右子链成本：计算 $A_{k+1}\times \cdots \times A_j$ 的最少乘法次数
   • 合并成本：将两个结果矩阵相乘的代价 = $p_{i-1}\times p_k\times p_j$
     • 左子链结果维度：$p[i-1]\times p[k]$
     • 右子链结果维度：$p[k]\times p[j]$
     • 合并乘法次数：$p[i-1]\times p[k]\times p[j]$

4. 尝试所有分割点：

   • 由于不知道哪个 $k$ 是最优的，需要尝试所有可能的分割点
   • 选择总成本最小的那个

$p$ 数组说明：$p$ 是维度数组，矩阵 $A_i$ 的维度是 $p[i-1]\times p[i]$。例如：$p=[6,11,7,15,3,21]$ 表示 $A_1$ 是 $6\times 11$，$A_2$ 是 $11\times 7$，等等。

---

2️⃣ 递推关系：自底向上计算

状态定义：

• $m[i,j]$：计算 $A_i\times A_{i+1}\times \cdots \times A_j$ 所需的最少标量乘法次数

递推公式：
m [ i , j ] = { 0 , if  i = j （单个矩阵，无需乘法） min ⁡ i ≤ k < j { m [ i , k ] + m [ k + 1 , j ] + p i − 1 × p k × p j } , if  i < j m[i,j] = \begin{cases} 0, & \text{if } i = j \quad \text{（单个矩阵，无需乘法）} \\ \min_{i \leq k < j} \{m[i,k] + m[k+1,j] + p_{i-1} \times p_k \times p_j\}, & \text{if } i < j \end{cases} m[i,j]={0,mini≤k<j​{m[i,k]+m[k+1,j]+pi−1​×pk​×pj​},​if i=j（单个矩阵，无需乘法）if i<j​

关键理解：

• 基础情况：$i=j$ 时，只有一个矩阵，成本为 $0$
• 递归情况：$i<j$ 时，尝试所有分割点 $k$，选择成本最小的

---

3️⃣ 计算过程：第n层使用n-1层的结果

动态规划的自底向上特性：按链的长度递增计算，确保计算 $m[i,j]$ 时，所有更短的子链已经计算完成。

计算顺序：

1. 第1层（长度 l = 1）：单个矩阵

   • $m[1,1],m[2,2],\dots ,m[n,n]=0$
   • 基础情况，直接得到

2. 第2层（长度 l = 2）：两个矩阵相乘

   • 计算 $m[1,2],m[2,3],\dots ,m[n-1,n]$
   • 使用第1层的结果：$m[i,i]$ 和 $m[j,j]$

3. 第3层（长度 l = 3）：三个矩阵相乘

   • 计算 $m[1,3],m[2,4],\dots ,m[n-2,n]$
   • 使用第1层和第2层的结果：$m[i,k]$ 和 $m[k+1,j]$（长度 ≤ 2）

4. …

5. 第n层（长度 l = n）：所有矩阵相乘

   • 计算 $m[1,n]$
   • 使用所有前面层的结果

关键点：

• 计算长度为 $l$ 的链时，需要用到长度 $<l$ 的链的结果
• 这保证了子问题已经求解，可以直接查表使用
• 避免了重复计算，每个子问题只计算一次

---

4️⃣ 两个表格：记录最优值和最优解

矩阵链乘法问题需要两个表格来完整解决问题：

表格1：$m[i,j]$ - 记录最小乘法次数

作用：存储子问题的最优值： $m[i,j]$ = 计算 $A_i\times \cdots \times A_j$ 的最少乘法次数

为什么需要：

• 避免重复计算相同的子问题
• 在计算 $m[i,j]$ 时，可以直接查表获取 $m[i,k]$ 和 $m[k+1,j]$ 的值

表格2：$s[i,j]$ - 记录最优分割位置

作用：存储子问题的最优解（用于回溯）。 $s[i,j]$ = 在计算 $A_i\times \cdots \times A_j$ 时的最优分割点 $k$

两个表格的关系：

• 在计算 $m[i,j]$ 时，同时更新 $s[i,j]$
• 当找到使 $m[i,j]$ 最小的 $k$ 时，记录 $s[i,j]=k$
• 回溯时，根据 $s[i,j]$ 递归地构造最优括号化方案

回溯过程：

如果 s[i,j] = k，则最优括号化是：
(A_i × ... × A_k) × (A_{k+1} × ... × A_j)

递归地：
- 左部分：根据 s[i,k] 继续分解
- 右部分：根据 s[k+1,j] 继续分解

---

🔍 算法执行过程示例

让我们用示例数据演示算法执行过程：

数据：5个矩阵，维度数组 $p=[6,11,7,15,3,21]$

步骤1：初始化（长度 l = 1）

单个矩阵的成本为 0：

$m[i,j]$	j=1	j=2	j=3	j=4	j=5
i=1	0 (6×11)
i=2		0 (11×7)
i=3			0 (7×15)
i=4				0 (15×3)
i=5					0 (3×21)

步骤2：计算长度为2的链（l = 2）

计算 $m[1,2]$（矩阵 A×B）：

• $k=1$：$m[1,1]+m[2,2]+p_0\times p_1\times p_2=0+0+6\times 11\times 7=462$
• $m[1,2]=462$，$s[1,2]=1$

计算 $m[2,3]$（矩阵 B×C）：

• $k=2$：$0+0+11\times 7\times 15=1155$
• $m[2,3]=1155$，$s[2,3]=2$

计算 $m[3,4]$（矩阵 C×D）：

• $k=3$：$0+0+7\times 15\times 3=315$
• $m[3,4]=315$，$s[3,4]=3$

计算 $m[4,5]$（矩阵 D×E）：

• $k=4$：$0+0+15\times 3\times 21=945$
• $m[4,5]=945$，$s[4,5]=4$

步骤3：计算长度为3的链（l = 3）

计算 $m[1,3]$（矩阵 A×B×C）：

• $k=1$：$m[1,1]+m[2,3]+p_0\times p_1\times p_3=0+1155+6\times 11\times 15=0+1155+990=2145$
• $k=2$：$m[1,2]+m[3,3]+p_0\times p_2\times p_3=462+0+6\times 7\times 15=462+0+630=1092$
• 最小值：$m[1,3]=1092$，$s[1,3]=2$

计算 $m[2,4]$（矩阵 B×C×D）：

• $k=2$：$0+315+11\times 7\times 3=546$
• $k=3$：$1155+0+11\times 15\times 3=1155+495=1650$
• 最小值：$m[2,4]=546$，$s[2,4]=2$

计算 $m[3,5]$（矩阵 C×D×E）：

• $k=3$：$0+945+7\times 15\times 21=0+945+2205=3150$
• $k=4$：$315+0+7\times 3\times 21=315+0+441=756$
• 最小值：$m[3,5]=756$，$s[3,5]=4$

步骤4：计算长度为4的链（l = 4）

计算 $m[1,4]$（矩阵 A×B×C×D）：

• $k=1$：$0+546+6\times 11\times 3=0+546+198=744$
• $k=2$：$462+315+6\times 7\times 3=462+315+126=903$
• $k=3$：$1092+0+6\times 15\times 3=1092+0+270=1362$
• 最小值：$m[1,4]=744$，$s[1,4]=1$

计算 $m[2,5]$（矩阵 B×C×D×E）：

• $k=2$：$0+756+11\times 7\times 21=0+756+1617=2373$
• $k=3$：$1155+945+11\times 15\times 21=1155+945+3465=5565$
• $k=4$：$546+0+11\times 3\times 21=546+0+693=1239$
• 最小值：$m[2,5]=1239$，$s[2,5]=4$

步骤5：计算长度为5的链（l = 5）

计算 $m[1,5]$（矩阵 A×B×C×D×E）：

• $k=1$：$0+1239+6\times 11\times 21=0+1239+1386=2625$
• $k=2$：$462+756+6\times 7\times 21=462+756+882=2100$
• $k=3$：$1092+945+6\times 15\times 21=1092+945+1890=3927$
• $k=4$：$744+0+6\times 3\times 21=744+0+378=1122$
• 最小值：$m[1,5]=1122$，$s[1,5]=4$

最终表格

$m[i,j]$ 表格（最小乘法次数）：

$m[i,j]$	j=1	j=2	j=3	j=4	j=5
i=1	0	462	1092	744	1122
i=2		0	1155	546	1239
i=3			0	315	756
i=4				0	945
i=5					0

$s[i,j]$ 表格（最优分割位置）：

$s[i,j]$	j=1	j=2	j=3	j=4	j=5
i=1	-	1	2	1	4
i=2		-	2	2	4
i=3			-	3	4
i=4				-	4
i=5					-

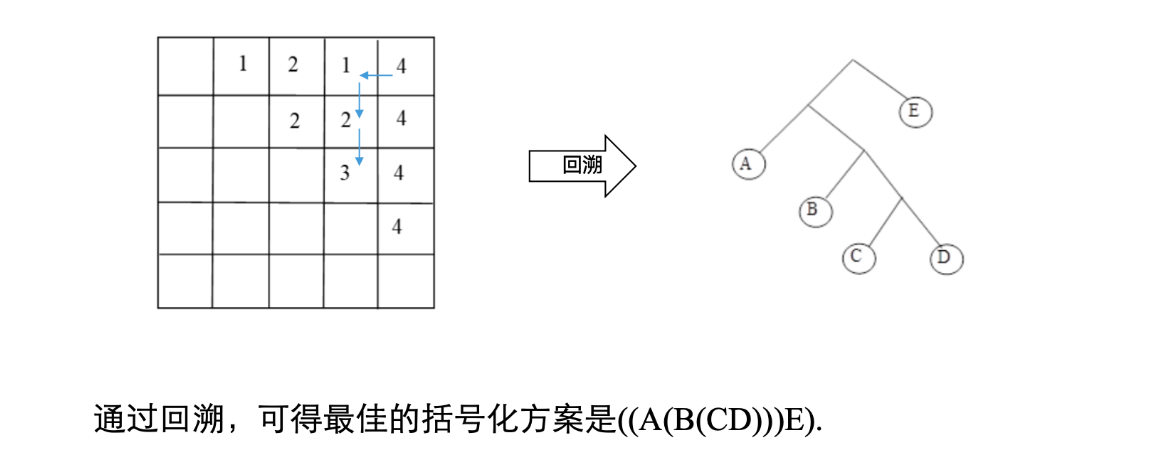
回溯构造最优解

回溯的核心逻辑：
$s[i,j]=k$ 表示：计算 $A_i\times \cdots \times A_j$ 时，最优分割点在位置 $k$。这意味着：先计算 $A_i\times \cdots \times A_k$，再计算 $A_{k+1}\times \cdots \times A_j$，最后合并

• 用括号表示：$(A_i\times \cdots \times A_k)\times (A_{k+1}\times \cdots \times A_j)$
• 然后递归地对左右两部分进行括号化

回溯过程（递归展开）：

第1步：处理整个链 $[1,5]$

查表：$s[1,5]=4$

含义：在位置4分割，得到：
$$(A_1\times A_2\times A_3\times A_4)\times (A_5)$$

当前状态：$(A_1{A}_2{A}_3{A}_4)\times A_5$

---

第2步：递归处理左部分 $[1,4]$

查表：$s[1,4]=1$

含义：在位置1分割 $A_1\times A_2\times A_3\times A_4$，得到：
$$(A_1)\times (A_2\times A_3\times A_4)$$

更新状态：$((A_1)\times (A_2{A}_3{A}_4))\times A_5$

---

第3步：递归处理 $[2,4]$

查表：$s[2,4]=2$

含义：在位置2分割 $A_2\times A_3\times A_4$，得到：
$$(A_2)\times (A_3\times A_4)$$

更新状态：$((A_1)\times ((A_2)\times (A_3{A}_4)))\times A_5$

---

第4步：简化括号

由于单个矩阵不需要括号，简化后得到：

最优括号化方案：$((A(B(CD)))E)$

其中：

• $A=A_1$
• $B=A_2$
• $C=A_3$
• $D=A_4$
• $E=A_5$

---

⚠️ 常见错误与注意事项

错误：维度数组索引错误

常见错误：

• 混淆矩阵编号（从1开始）和数组索引（从0开始）
• 计算合并成本时用错维度

正确理解：

• 矩阵 $A_i$ 的维度是 $p[i-1]\times p[i]$
• 计算 $A_i\times \cdots \times A_k$ 和 $A_{k+1}\times \cdots \times A_j$ 的合并成本：
  • 左结果矩阵维度：$p[i-1]\times p[k]$
  • 右结果矩阵维度：$p[k]\times p[j]$
  • 合并成本：$p[i-1]\times p[k]\times p[j]$

📊 算法复杂度分析

时间复杂度

递推关系：$T(n)=O(n^3)$

分析：

• 外层循环：链的长度 $l$ 从 2 到 $n$，共 $n-1$ 次
• 中层循环：起始位置 $i$ 从 1 到 $n-l+1$，平均约 $n/2$ 次
• 内层循环：分割点 $k$ 从 $i$ 到 $j-1$，平均约 $l/2$ 次
• 总时间复杂度：$O(n^3)$

💡 拓展思考

1. 为什么不能用贪心法？ 局部最优不等于全局最优，需要尝试所有可能的分割点。

2. 为什么时间复杂度是 $O(n^3)$？ 三层嵌套循环：长度、起始位置、分割点。

3. 如何优化？ 可以使用记忆化递归，但时间复杂度仍然是 $O(n^3)$。

4. 实际应用：编译器优化、数值计算、图像处理等领域都有应用。

---

💡 记忆口诀：矩阵链乘用DP，两个表格要记牢，m表记录最优值，s表回溯找方案！

 

习题2：钢条切割问题——动态规划

📌 适合对象：学习动态规划算法的同学
⏱️ 预计阅读时间：20-25分钟
🎯 学习目标：掌握如何用动态规划解决钢条切割问题，理解动态规划的两步：计算最优值和记录最优切割策略

---

📖 问题描述：最大化钢条切割收益

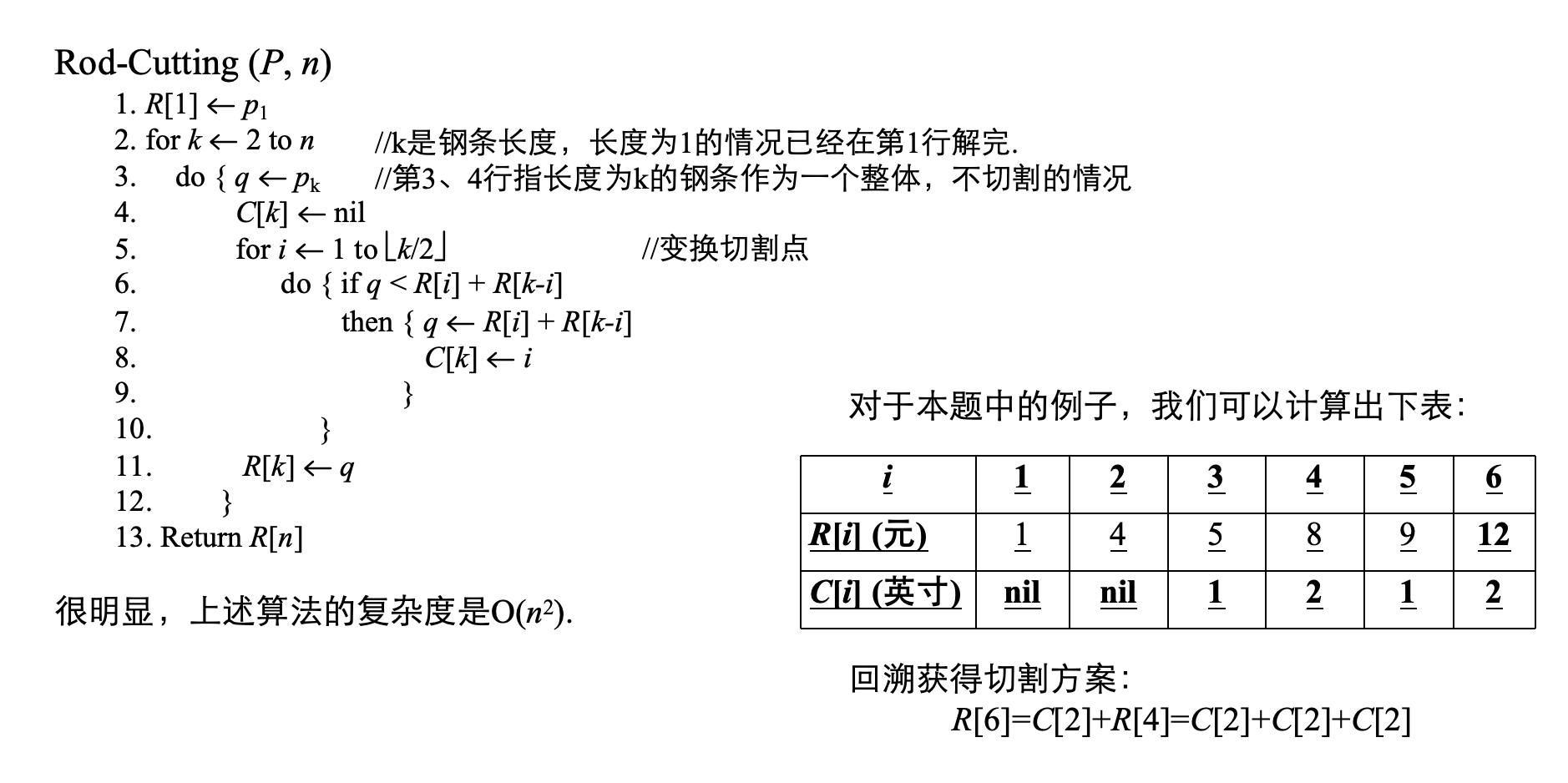
目标：

1. 设计动态规划算法，确定如何切割钢条以最大化总收益
2. 提供算法伪代码
3. 分析算法的时间复杂度和空间复杂度

---

正确思路：动态规划

动态规划的核心思想：将大问题分解为重叠子问题，自底向上求解，避免重复计算。

1️⃣ 问题分解的逻辑

分解思路：

1. 选择第一次切割位置：

   • 如果不切割：直接卖出，收益为 $p_k$
   • 如果切割：在位置 $i$（$1\le i\le k-1$）切割，得到：
     • 左段：长度为 $i$，收益为 $R[i]$（最优切割方案下的收益）
     • 右段：长度为 $k-i$，收益为 $R[k-i]$（最优切割方案下的收益）
     • 总收益：$R[i]+R[k-i]$

2. 最优子结构性质：

   • 如果长度为 $k$ 的钢条的最优切割方案是切割成 $i$ 和 $k-i$ 两段
   • 那么长度为 $i$ 和 $k-i$ 的钢条也必然采用最优切割方案
   • 否则，可以用更优的子方案替换，得到更优的整体方案（矛盾）

3. 尝试所有可能：

   • 尝试所有可能的第一次切割位置 $i$（$1\le i\le k-1$）
   • 比较：不切割的收益 $p_k$ 和所有切割方案的收益 $R[i]+R[k-i]$
   • 选择收益最大的方案

---

2️⃣ 递推关系：自底向上计算

状态定义：

• $R[k]$：切割长度为 $k$ 英寸的钢条能够带来的最大收益

基础情况：

• $R[1]=p_1$（长度为1的钢条，无法再切割，只能直接卖出）

递推公式：

R [ k ] = max ⁡ { max ⁡ 1 ≤ i ≤ k − 1 { R [ i ] + R [ k − i ] } , p k } R[k] = \max \left\{ \max_{1 \leq i \leq k-1} \{R[i] + R[k-i]\}, \quad p_k \right\} R[k]=max{1≤i≤k−1max​{R[i]+R[k−i]},pk​}

解释：

• 不切割：收益为 $p_k$
• 切割：尝试所有切割位置 $i$，选择 $R[i]+R[k-i]$ 的最大值
• 最终取两者的最大值

优化版本（利用对称性）：

由于切割成 $i$ 和 $k-i$ 与切割成 $k-i$ 和 $i$ 是等价的，可以只考虑 $i\le k/2$：

R [ k ] = max ⁡ { max ⁡ 1 ≤ i ≤ ⌊ k / 2 ⌋ { R [ i ] + R [ k − i ] } , p k } R[k] = \max \left\{ \max_{1 \leq i \leq \lfloor k/2 \rfloor} \{R[i] + R[k-i]\}, \quad p_k \right\} R[k]=max{1≤i≤⌊k/2⌋max​{R[i]+R[k−i]},pk​}

这样可以减少一半的计算量。

---

3️⃣ 计算过程：第k层使用1到k-1层的结果

动态规划的自底向上特性：按长度递增计算，确保计算 $R[k]$ 时，所有更短的钢条的最优收益已经计算完成。

计算顺序：

1. 第1层（长度 k = 1）：

   • $R[1]=p_1$
   • 基础情况，直接得到

2. 第2层（长度 k = 2）：

   • 计算 $R[2]$
   • 使用第1层的结果：$R[1]$
   • R [ 2 ] = max ⁡ { R [ 1 ] + R [ 1 ] , p 2 } R[2] = \max\{R[1] + R[1], p_2\} R[2]=max{R[1]+R[1],p2​}

3. 第3层（长度 k = 3）：

   • 计算 $R[3]$
   • 使用第1层和第2层的结果：$R[1]$ 和 $R[2]$
   • R [ 3 ] = max ⁡ { R [ 1 ] + R [ 2 ] , R [ 2 ] + R [ 1 ] , p 3 } = max ⁡ { R [ 1 ] + R [ 2 ] , p 3 } R[3] = \max\{R[1] + R[2], R[2] + R[1], p_3\} = \max\{R[1] + R[2], p_3\} R[3]=max{R[1]+R[2],R[2]+R[1],p3​}=max{R[1]+R[2],p3​}（利用对称性）

4. …

5. 第n层（长度 k = n）：

   • 计算 $R[n]$
   • 使用所有前面层的结果：$R[1],R[2],\dots ,R[n-1]$

关键点：

• 计算长度为 $k$ 的钢条时，需要用到长度 $<k$ 的钢条的最优收益
• 这保证了子问题已经求解，可以直接查表使用
• 避免了重复计算，每个子问题只计算一次

---

4️⃣ 两个表格：记录最优值和最优切割策略

钢条切割问题需要两个表格来完整解决问题：

表格1：$R[k]$ - 记录最大收益

作用：存储子问题的最优值

• $R[k]$ = 切割长度为 $k$ 的钢条能够带来的最大收益

为什么需要：

• 避免重复计算相同的子问题
• 在计算 $R[k]$ 时，可以直接查表获取 $R[i]$ 和 $R[k-i]$ 的值

表格2：$C[k]$ - 记录最优切割点

作用：存储子问题的最优解（用于回溯）

• $C[k]$ = 切割长度为 $k$ 的钢条时的最优第一次切割位置
• 如果 $C[k]=\text{nil}$，表示不切割（直接卖出整根钢条）

为什么需要：

• $R[k]$ 只告诉我们最优值是多少（最大收益是多少）
• $C[k]$ 告诉我们最优解是什么（如何切割才能达到这个最大收益）
• 没有 $C[k]$，无法构造出最优的切割方案

两个表格的关系：

• 在计算 $R[k]$ 时，同时更新 $C[k]$
• 当找到使 $R[k]$ 最大的切割位置 $i$ 时，记录 $C[k]=i$
• 如果 $p_k$ 更大，记录 $C[k]=\text{nil}$（不切割）
• 回溯时，根据 $C[k]$ 递归地构造最优切割方案

回溯过程：

如果 C[k] = nil，则长度为k的钢条不切割，直接卖出
如果 C[k] = i，则最优切割是：
  长度为i的钢条（根据C[i]继续切割）
  +
  长度为k-i的钢条（根据C[k-i]继续切割）

---

💻 算法伪代码

算法：Rod-Cutting(P[], n)
输入：价格数组P[1..n]，钢条长度n
输出：最大收益R[n]，最优切割策略

1. // 初始化：长度为1的钢条
2. R[1] ← P[1]
3. C[1] ← nil                    // 长度为1，无法切割
4.
4. // 自底向上计算
5. for k ← 2 to n do             // k是钢条长度，长度为1的情况已在第2行解决
6.     // 情况1：不切割，直接卖出
7.     q ← P[k]                   // 第3、4行指长度为k的钢条作为一个整体，不切割的情况
8.     C[k] ← nil
10.
9.    // 情况2：尝试所有切割位置
10.    for i ← 1 to ⌊k/2⌋ do      // 变换切割点（利用对称性，只需考虑i≤k/2）
11.        // 如果切割成i和k-i两段更优
12.        if q < R[i] + R[k-i] then
13.            q ← R[i] + R[k-i]
14.            C[k] ← i            // 记录最优切割点
15.        end if
16.    end for
19.
17.    R[k] ← q                   // 记录最大收益
18. end for
22.
19. return R[n]

---

🔍 算法执行过程示例

让我们用示例数据演示算法执行过程：

数据：$n=6$，价格表 $P=[1,4,4,7,8,9]$

步骤1：初始化（长度 k = 1）

• $R[1]=P[1]=1$
• $C[1]=\text{nil}$（长度为1，无法切割）

步骤2：计算长度 k = 2

• 不切割：$P[2]=4$
• 切割：
  • $i=1$：$R[1]+R[1]=1+1=2$
• 最大值： max ⁡ { 2 , 4 } = 4 \max\{2, 4\} = 4 max{2,4}=4
• $R[2]=4$，$C[2]=\text{nil}$（不切割更优）

步骤3：计算长度 k = 3

• 不切割：$P[3]=4$
• 切割：
  • $i=1$：$R[1]+R[2]=1+4=5$
  • $i=2$：（这里对称，结果一样）
• 最大值： max ⁡ { 5 , 4 } = 5 \max\{5, 4\} = 5 max{5,4}=5
• $R[3]=5$，$C[3]=1$（在位置1切割）

步骤4：计算长度 k = 4

• 不切割：$P[4]=7$
• 切割：
  • $i=1$：$R[1]+R[3]=1+5=6$
  • $i=2$：$R[2]+R[2]=4+4=8$
• 最大值： max ⁡ { 6 , 8 , 7 } = 8 \max\{6, 8, 7\} = 8 max{6,8,7}=8
• $R[4]=8$，$C[4]=2$（在位置2切割）

步骤5：计算长度 k = 5

• 不切割：$P[5]=8$
• 切割：（i是全局位置）
  • $i=1$：$R[1]+R[4]=1+8=9$
  • $i=2$：$R[2]+R[3]=4+5=9$
• 最大值： max ⁡ { 9 , 9 , 8 } = 9 \max\{9, 9, 8\} = 9 max{9,9,8}=9
• $R[5]=9$，$C[5]=1$（在位置1切割，$i=1$和$i=2$收益相同，选择较小的$i$）

步骤6：计算长度 k = 6

• 不切割：$P[6]=9$
• 切割：
  • $i=1$：$R[1]+R[5]=1+9=10$
  • $i=2$：$R[2]+R[4]=4+8=12$
  • $i=3$：$R[3]+R[3]=5+5=10$
• 最大值： max ⁡ { 10 , 12 , 10 , 9 } = 12 \max\{10, 12, 10, 9\} = 12 max{10,12,10,9}=12
• $R[6]=12$，$C[6]=2$（在位置2切割）

最终表格

$R[i]$ 表格（最大收益）：

$i$	1	2	3	4	5	6
$R[i]$（元）	1	4	5	8	9	12

$C[i]$ 表格（最优切割点）：

$i$	1	2	3	4	5	6
$C[i]$（英寸）	nil	nil	1	2	1	2

注意：i是全局位置。

---

回溯构造最优切割方案

回溯的核心逻辑：

• $C[k]=\text{nil}$ 表示：长度为 $k$ 的钢条不切割，直接卖出
• $C[k]=i$ 表示：长度为 $k$ 的钢条在位置 $i$ 切割，得到长度为 $i$ 和 $k-i$ 的两段
• 然后递归地对左右两段进行切割

回溯过程（递归展开）：

对于长度为6的钢条：

查表：$C[6]=2$

含义：在位置2切割，得到：

• 左段：长度为2
• 右段：长度为4

递归处理左段（长度为2）：

查表：$C[2]=\text{nil}$

含义：长度为2的钢条不切割，直接卖出

递归处理右段（长度为4）：

查表：$C[4]=2$

含义：在位置2切割，得到：

• 左段：长度为2
• 右段：长度为2

递归处理两个长度为2的段：

查表：$C[2]=\text{nil}$（两个都是）

含义：都不切割，直接卖出

最优切割方案：切割成 2英寸 + 2英寸 + 2英寸

总收益：$4+4+4=12$ 元 ✅

---

回溯算法伪代码

算法：Print-Optimal-Cut(C[], k)
输入：切割点数组C[]，钢条长度k
输出：打印最优切割方案

1. if C[k] == nil then
2.     print "长度为k的钢条不切割，直接卖出"
3. else
4.     i = C[k]
5.     print "在位置i切割，得到长度为i和k-i的两段"
6.     Print-Optimal-Cut(C, i)        // 递归处理左段
7.     Print-Optimal-Cut(C, k-i)     // 递归处理右段
8. end if

---

⚠️ 常见错误与注意事项

错误1：忘记考虑不切割的情况

错误做法：

# 错误：只考虑切割，忘记可以直接卖出
R[k] = max(R[i] + R[k-i] for i in range(1, k))

正确做法：

# 正确：同时考虑不切割和切割
R[k] = max(P[k], max(R[i] + R[k-i] for i in range(1, k)))

为什么重要：有时候不切割直接卖出可能比切割更优。

错误2：没有利用对称性优化

错误做法：

# 错误：尝试所有切割位置
for i in range(1, k):
    # 计算 R[i] + R[k-i]

正确做法：

# 正确：利用对称性，只需考虑 i ≤ k/2
for i in range(1, k//2 + 1):
    # 计算 R[i] + R[k-i]

为什么重要：切割成 $i$ 和 $k-i$ 与切割成 $k-i$ 和 $i$ 是等价的，可以减少一半的计算量。

---

📊 算法复杂度分析

时间复杂度

分析：

• 外层循环：长度 $k$ 从 2 到 $n$，共 $n-1$ 次
• 内层循环：切割位置 $i$ 从 1 到 $\lfloor k/2\rfloor$，平均约 $k/4$ 次
• 总时间复杂度：${\sum }_{k=2}^n\lfloor k/2\rfloor =O(n^2)$

递推关系：$T(n)=O(n^2)$

---

💡 拓展思考

1. 为什么不能用贪心法？ 局部最优不等于全局最优。例如，可能短段的单价更高，但最优方案可能是切割成长段。

2. 为什么时间复杂度是 $O(n^2)$？ 两层嵌套循环：长度和切割位置。

3. 实际应用：

   • 资源分配：如何将有限资源分配给不同项目以最大化收益
   • 投资组合：如何分配资金到不同投资项目
   • 生产计划：如何安排生产以最大化利润

4. 与矩阵链乘法的对比：

   • 相似点：都是动态规划，都需要记录最优值和最优解
   • 不同点：矩阵链乘法是 $O(n^3)$，钢条切割是 $O(n^2)$

---

💡 记忆口诀：钢条切割用DP，两个表格要记牢，R表记录最优值，C表回溯找方案，自底向上O(n²)，最大收益轻松算！