文章目录
- 大数定理是描述随机变量序列的前一些项的算数平均值在某种条件下收敛到这些项的均值的算术平均值;
- 中心极限定理则是确定在什么条件下,大量随机变量之和的分布逼近于正态分布。
一. 大数定理
大量实验证实,随机事件的频率 f n ( A ) {f_n(A)} fn(A)当重复实验的次数n增大时总呈现出稳定性,稳定在某 一个常数的附近。
1. 弱大数定律:样本均值趋近于总体均值

大数法则说明的是:在重复进行大量独立同分布的随机试验时,样本均值趋近于总体均值。
2. 伯努利大数定理:频率趋近于概率

- 伯努利大数定理说明:在n充分大时,事件频率与概率的偏差小于任意小值,这件事几乎是确定事件,这就是频率稳定性。
- 在实际应用过程中,当试验次数很大时可以用事件的频率代替事件发生的概率。
二. 中心极限定理:正态分布的趋近
中心极限定理描述了在一定条件下,样本均值的分布趋近于正态分布。
中心极限定理为统计推断提供了理论基础,使得我们可以在样本量较大的情况下使用正态分布近似样本均值的分布,从而应用各种统计方法(如假设检验和置信区间估计)。
1. 独立同分布的中心极限定理:均值趋近正态分布
随机变量相互独立,服从同一分布,当n充分大时,算术平均满足如下:
这就是说,均值 μ \mu μ,方差 σ 2 > 0 \sigma{^2} >0 σ2>0,的独立同分布的随机变量 X 1 , X 2 , X 3 . . . , X n X_1,X_2,X_3...,X_n X1,X2,X3...,Xn的算术平均 X ˉ = 1 / n ∑ k = 1 n X k \bar{X}=1/n\sum_{k=1}^{n}X_k Xˉ=1/n∑k=1nXk,当n充分大时近似的服从均值为μ,方差为σ²/n的正态分布。
这一结果是数理统计中大样本统计推断的基础。
2. 李雅普诺夫定理:随机变量的和趋近于正态分布
主要涉及随机变量的和的分布趋近于正态分布的条件
李雅普诺夫定理的条件
在条件下:新的随机变量服从标准正态分布
3. 棣莫弗 一 拉普拉斯中心极限定理:二项分布的极限分布是正态分布

二项分布的极限分布是正态分布
当n充分大时,我们可以利用(2.5)式来计算二项分布的概率.





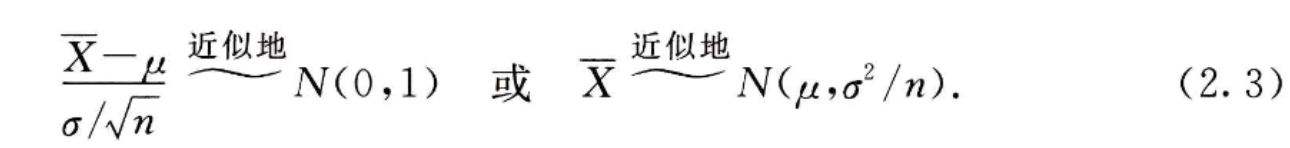



















 769
769

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










