从数组到堆：完全二叉树的 “顺序存储” 实现秘籍

前言：

        在之前的讨论中，我们已经了解了树这种非线性数据结构，并重点介绍了完全二叉树和满二叉树这两种特殊形式。本文将基于完全二叉树的特性，进一步探讨与之密切相关的重要数据结构——堆。

---

        

一、完全二叉树的回顾

        

         完全二叉树：除最后一层外，每一层的节点数均达到最大值，最后一层的节点从左到右连续排列，缺失的节点只能在右侧。

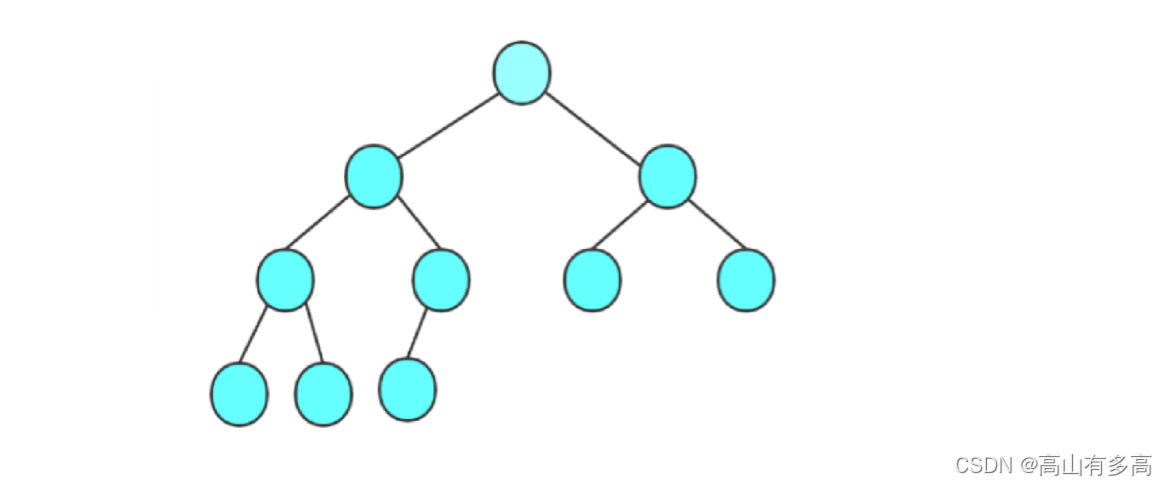
对于完全二叉树，满足如下特征：

        

①叶子节点仅可能出现在最下两层，且最下层叶子一定靠左集中。

        

②由于节点连续排列的原因，适合用数组存储，无需额外空间记录指针，通过索引即可计算父子节点位置。

        

③不存在只有右子节点而无左子节点的节点，右子节点存在的前提是左子节点已存在。        

        

注：满二叉树也被视为特殊的完全二叉树。

        

二、堆的引入

        

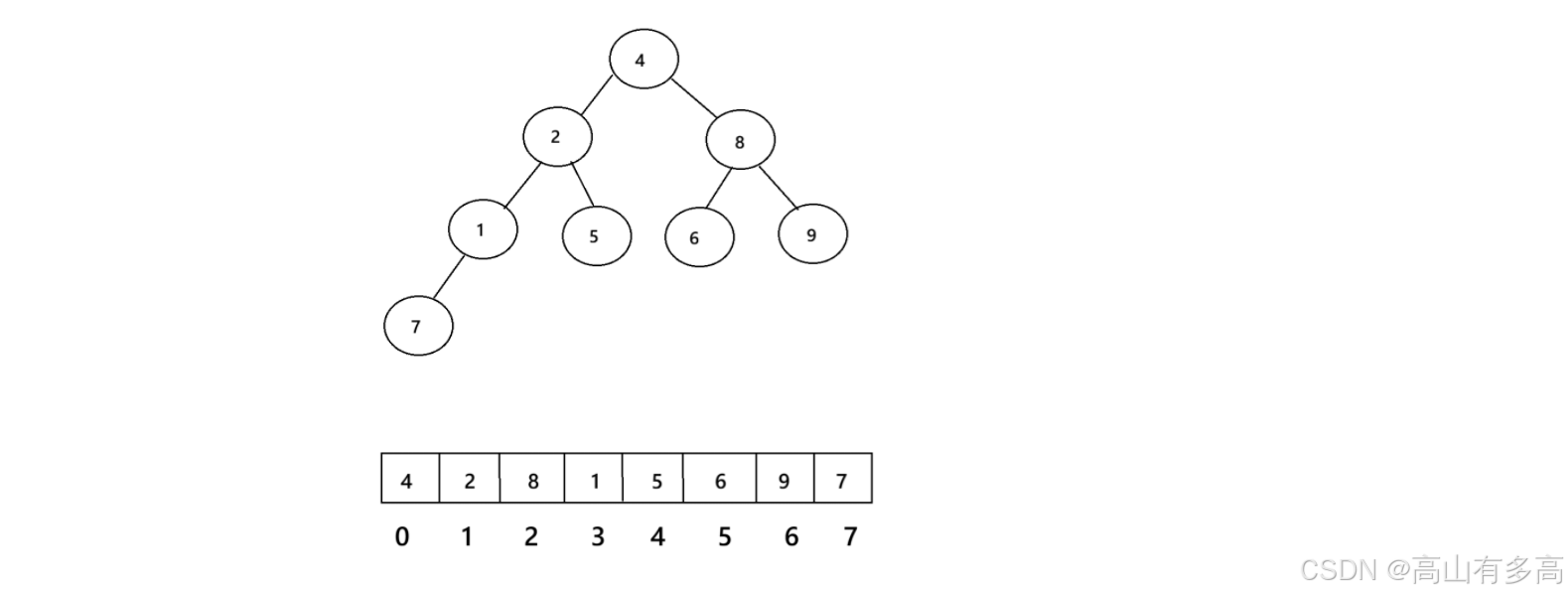
        根据完全二叉树的特点：叶子节点只出现在最下面两层，且最下层的叶子节点都集中在左侧。得益于这种连续排列的特性，我们可以用数组来存储完全二叉树，从而形成一种新的数据结构——堆。

        堆在逻辑结构上采用完全二叉树的组织形式，但在计算机底层存储中，实际上是通过一段连续的数组空间来实现的。

        

 如下图所示，完全二叉树所形成的堆：

  如图所示：普通二叉树所形成的堆      

        

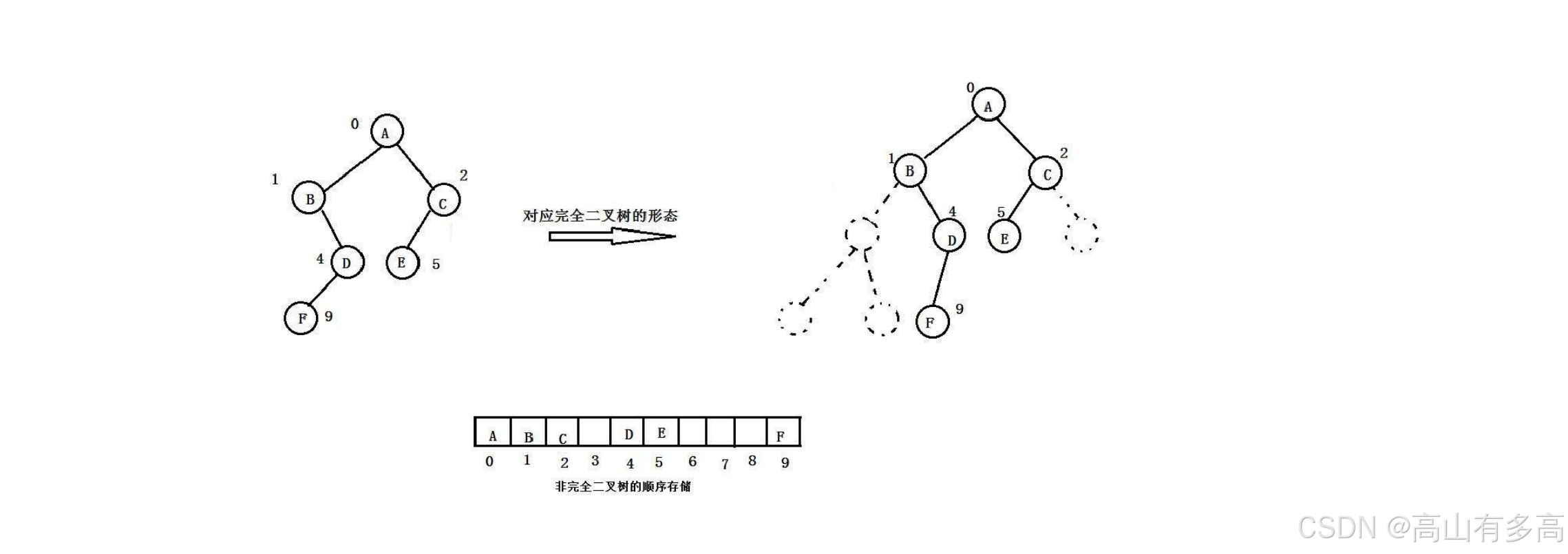
普通的二叉树并不适合用数组存储，因为其节点并不是连续，会造成大量空间浪费。相比之下，完全二叉树更适于采用顺序结构存储。

        

在实际应用中，我们常用数组来存储堆（一种特殊的二叉树结构）。

        

需要注意的是，这里的堆与操作系统虚拟地址空间中的堆是两个不同概念：前者属于数据结构范畴，后者则是操作系统管理内存的一块特定区域。

        

三、堆的分类     

        
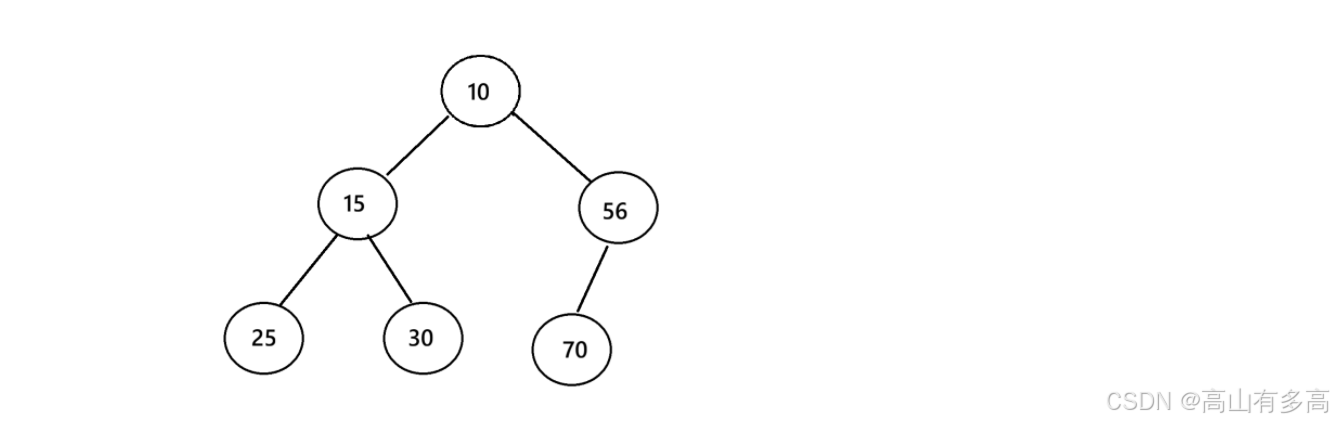
        任何一个完全二叉树，根节点（父节点）上的数据和孩子节点上的数据之间是存在一种关系的。根据这种关系堆又可以分为大堆和小堆。         

①大堆：父亲节点的数据 >= 左右两个孩子节点的数据，注意：左右子节点之间（即兄弟节点之间）无大小要求。

如下图所示：

        

        

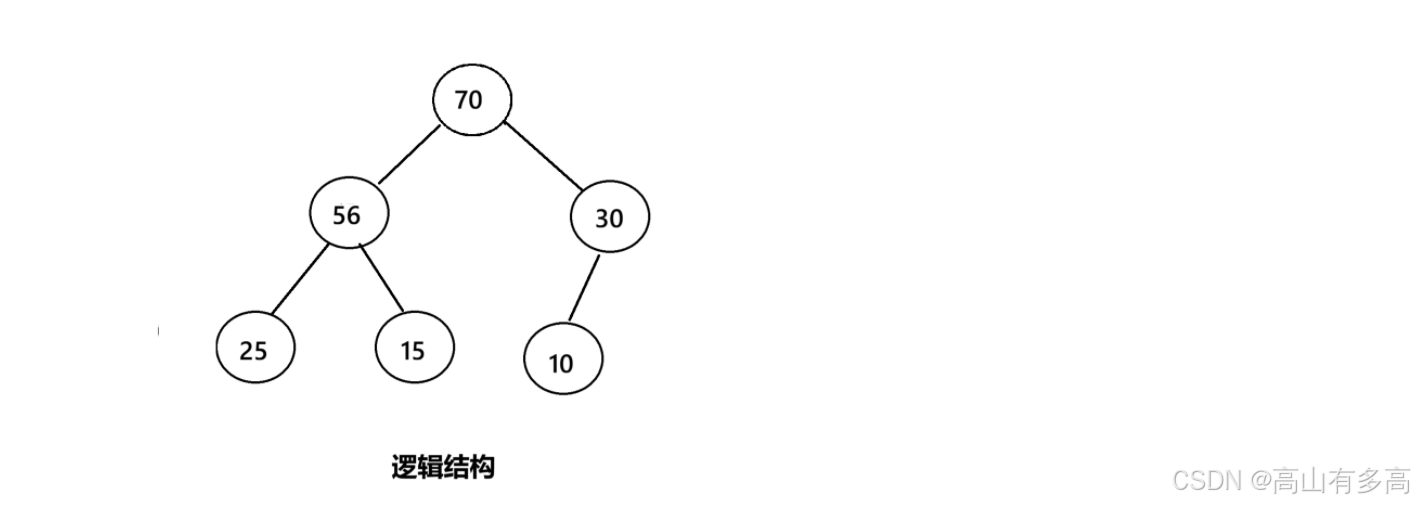
②小堆:父亲节点上的数据<=左右孩子节点上的数据，注意：左右子节点之间无大小要求。

如下图所示：

        

四、堆的性质

        

4.1堆的共性特点

        

（1）逻辑结构上：堆是一棵完全二叉树，物理上通过数组的形式进行存储。

        

（2）父子节点满足如下关系：

         1.若父节点的索引为 i，则左子节点的索引为：2 * i + 1 , 右子节点的索引为：2 * i + 2。

         2.若孩子节点的索引为 j，则父亲节点的索引为：( j - 1 ) / 2。

        

温馨提示：这里并不用去区分孩子节点是左节点还是右节点 , 如下图所示：

        

        

以数值为2的父亲节点为例，其下标为1:

        

左孩子节点数值为1，下标为3;  右孩子节点数值为5,下标为4。            

        

通过左孩子节点下标计算父亲节点下标： ( 3 - 1 ) / 2 = 1        

        

通过右孩子节点下标计算父亲节点下标： (4 - 1) / 2 = 1 

        

因为整数除法，有向零取整的原因，故而无论是左孩子节点还是右孩子节点通过（j - 1）/ 2 都能计算得到父亲节点的下标。

         

（3）无全局有序性：堆仅保证了“父亲节点和孩子节点”的大小关系，而并没有保证兄弟节点的大小关系。

        

4.2小堆的特性

        

（1）堆序性约束：每个父节点的值 ≤ 其左右子节点的值（左右子节点之间无大小要求）。

        

（2）堆顶特性：堆的根节点（数组第一个元素，索引 0）是整个堆中的最小值—— 可快速获取全局最小值（时间复杂度 O(1) ）。

        

4.3大堆的特性

        

（1）堆序性约束：每个父节点的值 ≥ 其左右子节点的值（注意：左右子节点之间无大小要求）。

        
（2）堆顶特性：堆的根节点（数组第一个元素，索引 0）是整个堆中的最大值—— 这是大堆最关键的特性，可快速获取全局最大值（时间复杂度 O(1) ）。

         

           

五、堆的实现 

        

实现堆的文件如下图所示：

        

实现堆有关的函数接口如下图所示：     

        

 实现堆的两个核心算法：       

        

1.堆的两个重要算法

        

两个算法的共同目标：让破坏堆性质的节点，通过“移动”回到满足堆性质的位置。

        

前提铺垫：堆是一棵完全二叉树，用数组存储时的节点关系是整个算法的基础。

                 下面规定：parent为父亲节点的下标       child为孩子节点的下标

        

 ①父亲节点的索引：parent = (child - 1 )  /  2。

        

②左孩子节点的索引：leftchild=2 * parent + 1。

        

③右孩子节点的索引：rightchild=2 * parent + 2。

            

        

1.1向上调整算法

        场景实例：假设现在存在一个小堆，要向堆中插入一个元素，并维持堆的结构。

        

核心逻辑：

            新元素插入堆尾后，它的父节点可能比新插入子节点小 —— 让新元素“ 上浮 ”，与父节点交换，直到它比父节点小，或浮到根节点（堆顶）。

             简而言之，对于向上调整算法的核心思维就是：当子节点可能比父节点 “更合适”时，需要让子节点往上浮，找到合适位置。        

        

实例分析：

        

一、如上图所示，由于新插入的子节点的值为  10  与 其父亲节点的值 28 相比 不满足小堆的关系，所以我们需要让子节点向上浮动，直到它比父节点更小，或者一直向上浮动到根节点为止。

        

        

二、详解向上调整的过程

        

( 1 ) 上图中原来的小堆为: [15 , 18 , 19 , 25 , 28 , 34 , 65 , 49 , 27 , 37] ，堆中元素个数size=10，现需要插入一个元素 10 （放在堆尾索引为10的位置处）

       

( 2 ) 新插入的子节点的索引为 child = 10  插入后小堆变为：   [15 , 18 , 19 , 25 , 28 , 34 , 65 , 49 , 27 , 37，10]

        计算得到其父亲节点的索引为  parent=( child - 1 ) / 2  , 即索引为4 ，arr[4]=28。

        

( 3 )比较arr[child] 与 arr[parent] 的值，由于要维持小堆，所以当arr[child] < arr [parent] 时，就要对子节点和父亲节点进行交换

      交换后的小堆变为： [15 , 18 , 19 , 25 , 10 , 34 , 65 , 49 , 27 , 37，28]

        

( 4 )更新孩子节点的索引和父亲节点的索引：child=parent ;   parent=(child-1) / 2 ;

        

( 5 ) 重复这个过程，直到满足新插入的子节点比父节点更小，或者一直向上浮动到根节点为止，所以我们可以通过循环进行描述上述三个步骤。

        

三、 向上调整代码实现如下：

void AdjustUp(HPDataType* a, int child)
{
	//已知孩子节点的下标为child
	//父亲节点下标为:(child-1)/2

	//初始时父亲节点的下标
	int parent = (child - 1) / 2;

	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			//进行交换
			swap(&a[child], &a[parent]);
    
			//更新孩子节点的下标
			child = parent;

            //更新父亲节点的下标
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}

    //退出条件为：
    //1.子节点比父节点大    
    //2.子节点到达根的位置
}

        

四、若原来是大堆，只需把比较符号反转,将 “<” 变为 “>”, 即当前节点 > 父节点（大根堆性质破坏），则交换并继续上浮。

        

             

五、向上调整算法的时间复杂度分析：

        由于堆是一棵完全二叉树，对于完全二叉树的高度h，满足h≈log2(N) ，最坏的情况下，需要从叶节点一直到根节点，向上浮动h次，故而向上调整算法的时间复杂度为O（logN）。

---

        

1.2 向下调整算法        

        

        场景实例：假设现在存在一个小堆，若堆顶元素被一个更大的值替代，并维持堆的结构。

        

核心思维：当父节点位置可能比子节点位置“不合适”时，需要让父节点往下沉，找到合适位置。

        

实例分析：   

                  

 一、如上图所示，原堆顶元素5被更大的元素27替换后，破坏了小堆性质。

        

        此时父节点位置已不满足条件，所以需要通过向下调整操作，直到它比子节点更小，或者到达叶节点位置

     （温馨提示：判断是否到达叶节点位置，即只需要判断其子节点不在堆的范围内，循环的停止条件）。

        

二、详解向下调整的过程

        

( 1 ) 上图中原来的小堆为：[5，15，19，18，28，34，65，49，25，37] ，但是堆顶元素被替换为27，

        则现在的小堆变为：[27，15，19，18，28，34，65，49，25，37],此时堆中的元素不在满足小堆的特性，需要进行向下调整。

        

( 2 )  此时父亲节点的索引为：parent=0，

        其左孩子节点的索引为：leftchild=parent * 2 + 1 ，其右孩子节点的索引为：rightchild=parent*2+2。

        我们不能确定左孩子节点的值与右孩子节点的值的大小关系，所以需要进行比较确定出其中最小的一个。

        这里可以通过假设法，不用单独区分左孩子节点的索引和右孩子节点的索引，只需定义一个子节点索引child，然后假设左孩子节点的值最小，若左孩子节点的值大于右孩子节点的值，即右孩子节点的更小，仅需要对child++即可找到右孩子节点。

        

( 3 ) 比较arr[parent]与arr[child]的值，由于需要维持小堆，如果arr[parent]>arr[child],需要对父节点和子节点进行交换。

        交换后的小堆为：[15，27，19，18，28，34，65，49，25，37]

        

( 4 ) 更新parent的索引和child的索引：parent=child; child=parent * 2 + 1; 

        

( 5 ) 重复这个过程，直到它比子节点更小，或者到达叶节点位置（叶节点位置处满足：子节点不在堆的范围内）。

        

三、向下调整代码的实现：

        

void AdjustDown(HPDataType* a, int size, int parent)
{

	//父亲节点下标：parent
	//左孩子节点下标为：parent*2+1
	//右孩子节点下标为：parent*2+2

	//假设左孩子是最小的
	int child = parent * 2+1;
    
	while (child < size)
	{
        //保证child+1在有效范围
		if (child+1 < size && a[child + 1] < a[child] )
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			//交换父亲节点和孩子节点
			swap(&a[child], &a[parent]);
			//更新父亲节点
			parent = child;
			//更新孩子节点
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}

    //退出循环的条件
    1.父节点无子节点，即到达了叶节点位置，通过不满足while循环条件退出
    2.父节点的值 < 子节点的值，通过break退出
}

        

四、若原来是大堆，只需把比较符号反转,将 “<” 变为 “>”, 即当前节点 > 父节点（大根堆性质破坏），则交换并继续下浮。

        

五、向下调整算法的时间复杂度分析：

        

单个节点的向下调整，最坏情况是从根节点下沉到最底层叶子节点，下沉层数 = 堆的高度 - 1 = O(log n)。

        

每一层的操作（比较父节点与两个子节点、交换）都是常数时间 O(1)，因此总时间复杂度由下沉层数决定

        

故而单个节点向下调整时间复杂度为O（logN）。

        

2.Heap.h文件的实现

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
	
typedef int HPDataType;
	
typedef struct Heap
{
	HPDataType* a;

	int size;
	int capacity;

}Heap;

void HPInit(Heap* php);

void HPDestroy(Heap* php);

void HPPush(Heap* php, HPDataType x);

void HPPop(Heap* php);

HPDataType HPTop(Heap* php);

bool HPEmpty(Heap* php);

     

在Heap.h文件中，我们重点要关注堆的声明：

        

typedef int HPDataType;
	
typedef struct Heap
{
	HPDataType* a;

	int size;
	int capacity;

}Heap;

首先对堆存储的元素进行重命名，方便后续元素类型的更换 ： typedef int HPDataType;            

        

成员一：HPDataType* a;         堆底层通过数组存储

        

成员二：int size;        堆中元素的个数

        

成员三：int capacity   堆的容量

        

3.Heap.c文件的实现

        

3.1堆的初始化

        

void HPInit(Heap* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;
}

        

3.2堆的销毁

        

void HPDestroy(Heap* php)
{
	assert(php);

	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

        

3.3堆的插入

        

//在堆中插入一个元素
void HPPush(Heap* php, HPDataType x)
{
	assert(php);

	//空间是否足够
	if (php->size == php->capacity)
	{
		//进行扩容
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}

	php->a[php->size] = x;
	php->size++;

	//运用向上调整算法-建小堆
	AdjustUp(php->a, php->size-1);

}

        

1.向堆中插入一个元素，优先判断是否容量足够，若容量不够，需要进行扩容处理。

        

        

2.插入一个元素后，进行向上调整，建立小堆，事实上向上调整的过程也可以视作建堆的过程。

        

 3.4堆的删除

        

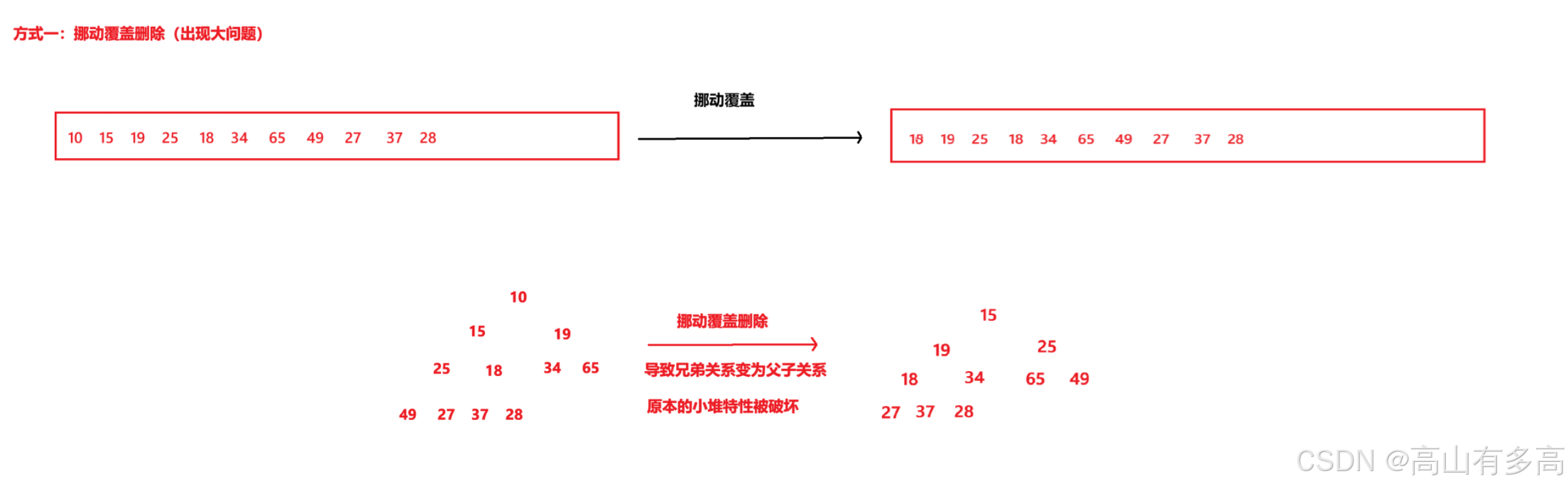
对于堆的删除，我们进行的是删除堆顶元素后，依然维持堆的结构，如果采用暴力的挪动覆盖删除：

① 一方面，时间复杂度高，删除一个栈顶元素需要挪动堆中的所有元素。

②另一方面，堆的特性被破坏，父子节点的关系混乱。

        

        

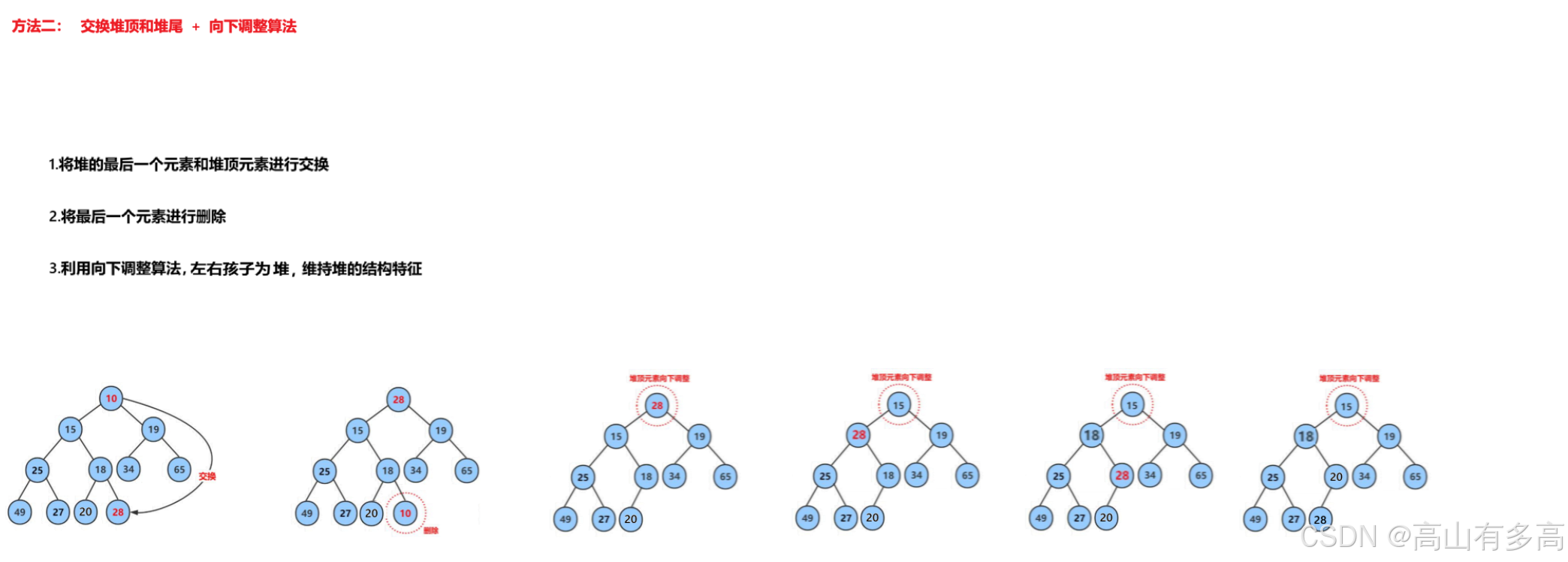
对于堆的删除，我们可以通过交换+向下调整的方式：

        

//删除堆顶元素，使得删除元素后仍然为堆结构
void HPPop(Heap* php)
{
	assert(php);
	assert(php->size > 0);

	//交换堆顶元素和堆的最后一个元素
	swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;

	//向下调整算法
	if (php->size > 0)
	{
		AdjustDown(php->a, php->size, 0);
	}

}

        

 3.5取堆顶元素

HPDataType HPTop(Heap* php)
{
	assert(php);
	assert(php->size > 0);

	return php->a[0];
}

        

3.6判断堆是否为空

bool HPEmpty(Heap* php)
{
	assert(php);
	return php->size == 0;
}

        

4.Test.c文件的实现

        

#include "Heap.h"

// 测试样例1：基本插入与堆顶获取
void TestHeap1() 
{
    printf("=== TestHeap1: 基本插入与堆顶获取 ===\n");
    Heap hp;
    HPInit(&hp);

    // 插入元素：3,1,2
    HPPush(&hp, 3);
    printf("插入3后，堆顶为：%d（预期：3）\n", HPTop(&hp));

    HPPush(&hp, 1);
    printf("插入1后，堆顶为：%d（预期：1）\n", HPTop(&hp));

    HPPush(&hp, 2);
    printf("插入2后，堆顶为：%d（预期：1）\n", HPTop(&hp));

    // 验证堆非空
    printf("堆是否为空：%s（预期：false）\n", HPEmpty(&hp) ? "true" : "false");

    HPDestroy(&hp);
    printf("------------------------------------\n\n");
}

// 测试样例2：删除堆顶与堆结构维护
void TestHeap2()
{
    printf("=== TestHeap2: 删除堆顶与堆结构维护 ===\n");
    Heap hp;
    HPInit(&hp);

    // 插入元素：5,3,4,1,2（构建小堆）
    HPPush(&hp, 5);
    HPPush(&hp, 3);
    HPPush(&hp, 4);
    HPPush(&hp, 1);
    HPPush(&hp, 2);
    printf("插入5,3,4,1,2后，堆顶为：%d（预期：1）\n", HPTop(&hp));

    // 删除堆顶（1），新堆顶应为2
    HPPop(&hp);
    printf("删除堆顶后，堆顶为：%d（预期：2）\n", HPTop(&hp));

    // 再删除堆顶（2），新堆顶应为3
    HPPop(&hp);
    printf("再删除堆顶后，堆顶为：%d（预期：3）\n", HPTop(&hp));

    // 再删除堆顶（3），新堆顶应为4
    HPPop(&hp);
    printf("再删除堆顶后，堆顶为：%d（预期：4）\n", HPTop(&hp));

    HPDestroy(&hp);
    printf("------------------------------------\n\n");
}

// 测试样例3：边界情况（空堆、单次插入删除）
void TestHeap3( )
{
    printf("=== TestHeap3: 边界情况测试 ===\n");
    Heap hp;
    HPInit(&hp);

    // 空堆判空
    printf("初始堆是否为空：%s（预期：true）\n", HPEmpty(&hp) ? "true" : "false");

    // 插入单个元素
    HPPush(&hp, 10);
    printf("插入10后，堆顶为：%d（预期：10）\n", HPTop(&hp));
    printf("堆是否为空：%s（预期：false）\n", HPEmpty(&hp) ? "true" : "false");

    // 删除唯一元素
    HPPop(&hp);
    printf("删除唯一元素后，堆是否为空：%s（预期：true）\n", HPEmpty(&hp) ? "true" : "false");

    // （注意：以下代码会触发断言失败，仅用于验证边界检查，实际测试可注释）
    // printf("空堆获取堆顶：");
    // HPTop(&hp); // 断言失败（size为0）

    HPDestroy(&hp);
    printf("------------------------------------\n\n");
}

// 测试样例4：扩容与批量操作（超过初始容量）
void TestHeap4()
{
    printf("=== TestHeap4: 扩容与批量操作 ===\n");
    Heap hp;
    HPInit(&hp);

    // 插入6个元素（初始容量为4，会触发扩容）
    int arr[] = { 6, 5, 7, 8, 9, 0 };
    for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) 
    {
        HPPush(&hp, arr[i]);
        printf("插入%d后，堆顶为：%d\n", arr[i], HPTop(&hp));
    }
    // 预期堆顶变化：6 →5 →5 →5 →5 →0

    // 批量删除堆顶，验证是否按升序弹出（小堆特性）
    printf("批量删除堆顶（预期顺序：0,5,6,7,8,9）：");
    while (!HPEmpty(&hp))
    {
        printf("%d ", HPTop(&hp));
        HPPop(&hp);
    }
    printf("\n");

    HPDestroy(&hp);
    printf("------------------------------------\n\n");
}

int main() 
{
    TestHeap1();
    TestHeap2();
    TestHeap3();
    TestHeap4();
    return 0;
}

        

既然看到这里了，不妨关注+点赞+收藏，感谢大家，若有问题请指正。