平面上有两个圆相交，求两个圆相交部分的面积

平面上有两个圆相交，求两个圆相交部分的面积

又学习了一遍算法，感触颇深，也对算法有了更进一步的认识，记录一下这次的学习，希望能帮到有需要的人。
输入：六个参数：第一个圆的圆心坐标，半径，第二个圆的圆心坐标，半径。
输出：返回相交部分的面积，若不相交，则返回0，并提示两圆无相交。
分析：平面上有两个圆相交，求两个圆相交部分的面积，如下图所示。

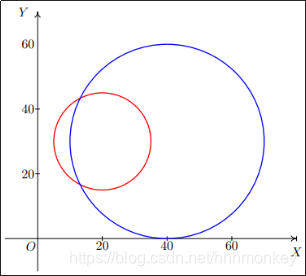
首先，需要判断两个圆是否相交，若不相交，则返回0，若相交，则要求出相交部分的面积，可以用两个扇形的面积减去四边形的面积，其中，两个扇形分别为两个圆心与两个圆相交点所组成的扇形，四边形则是两个圆心与相交点所构成的四边形。需要注意的是，这里的四边形不一定为凸四边形，所以这里的四边形面积可以利用海伦公式来进行计算，其次，这里扇形的圆心角不一定为锐角，所以，在计算扇形面积的时候，可以利用余弦定理来进行计算。
其中，海伦公式为：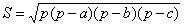
，其中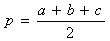
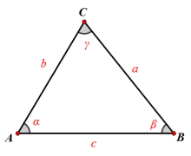
，，a、b、c分别为平面内三角形三边边长。余弦定理为：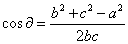
，其中各个字母表示如下图所示：

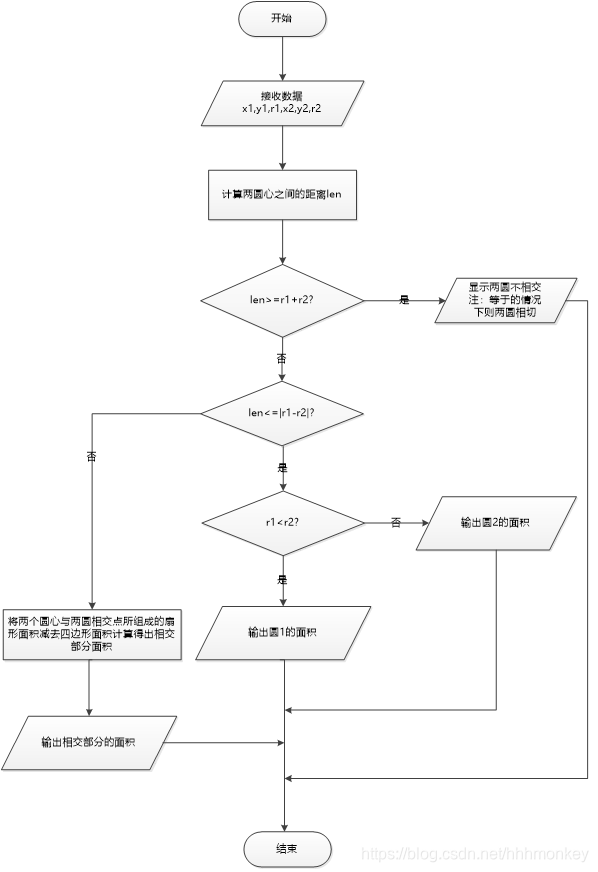
程序流程图如下：

public class IntersectionCircles {
	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		double x1 = scanner.nextDouble();
		double y1 = scanner.nextDouble();
		double r1 = scanner.nextDouble();
		double x2 = scanner.nextDouble();
		double y2 = scanner.nextDouble();
		double r2 = scanner.nextDouble();
		double s = instersection(x1,y1,r1,x2,y2,r2);
		if(s==0){
			System.out.println("两个圆不相交！");
		}else{
			System.out.println("两个圆相交的面积等于："+s);
		}
		scanner.close();
	}

	private static double instersection(double x1,double y1,double r1,double x2,double y2,double r2){
		double p,s;
		double ans;//表示相交的面积
       //表示两圆心之间的距离
		double len = Math.sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1)); 
		if(len >= r1+r2){//表示两圆不相交
			ans = 0;
		}else if(len <= Math.abs(r1-r2)){//包含了
			if(r1 < r2){
				ans = Math.PI*r1*r1;
			}else{
				ans = Math.PI*r2*r2;
			}
		}else{
			p = (len+r1+r2)/2;
			s = 2*Math.sqrt(p*(p-len)*(p-r1)*(p-r2));//海伦公式求四边形面积
			//余弦定理求扇形面积
ans=Math.acos((r1*r1+len*len-r2*r2)/(2*r1*len))*r1*r1+Math.acos((r2*r2+len*len-r1*r1)/(2*r2*len))*r2*r2-s;
		}
		return ans;
	}
}