Codeforces 432D 完美子串 + 51nod 1129 字符串最大值（dp-kmp）

最新推荐文章于 2021-08-26 00:27:19 发布

原创最新推荐文章于 2021-08-26 00:27:19 发布 · 601 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#kmp #dp

-------dp------- 同时被 3 个专栏收录

11 篇文章

订阅专栏

kmp。

2 篇文章

订阅专栏

------字符串-------

1 篇文章

订阅专栏

本文深入探讨了KMP算法的应用及其实现细节，特别是在字符串匹配问题中的高效解决方案。通过实例讲解了如何利用KMP算法求解特定字符串问题，并详细解释了next数组的作用与计算方法。

这里写图片描述

~~我觉得我能A这题完全是因为前一天晚上做了很类似的。~~

字符串，前缀后缀，出现次数，关键词一拼就是kmp。
首先我们考虑第二问的第二个数，怎么求得一段前缀子串在 s 中出现的次数。这里需要我们深入地了解next数组的含义。

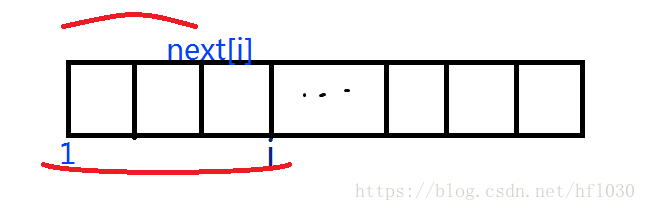
这里写图片描述

呃，我的意思是，如果 s[ 1~i ]出现过x次，那么 s[ 1~next[ i ] ]也必然至少出现过x次。
由此，我们设 d[ i ]表示 s[ 1~i ]出现的次数，可得推导方程：
d[ next[ i ] ]+= d[ i ];

刘汝佳在《入门经典》里讲DAG上的dp的时候好像说过，这种 “‘对于每个状态 i，更新 d[ i ]所影响到的状态 j’的方法称为刷表法。因为这不是一个可以直接计算 d[ j ]的方程，所以只称它为更新公式“。当时不太理解，现在才有点明白了。

注意，这里递推的时候需要倒序，理由十分直观，next[ i ]必然在 i 的前面，倒推能保证 d[ i ]一定被更新完毕。

51nod 1129 字符串最大值那道题至此已经可以解决了。

好了，那么看第一问和第二问第一个数。
next[ len ] 表示 s[ 1~next[ len ] ] 和 s[ len-next[ len ]+1,len ]是相同的，所以它必然是符合题意的，而且是最长的那一个。那么 next [ next[ len ] ]呢？根据 next 数组的定义，它是 s[ 1~next[ len] ]的前缀，也是它的后缀，也是 s[ len-next[ len ]+1,len ] 的后缀，即，它是 s 的后缀，所以这也是满足题意的。
所以，这一问的正解就是无限跳跳跳，不停地 next[ next[ next[ ….] ] ]，cnt++,直到 next 为0。这个过程中，把符合题意的前缀子串长度记录下来，只需要输出这个值 x 以及它对应的 d[ x ] 就是答案啦。

深入理解 next ，它真的好强。

char s[100010];
int lens;
int next[100010];
int d[100010];
int ans;

bool f[100010];//f[i]表示长度为i的前缀子串是否合法。

void kmp_()
{
    memset(next,0,sizeof(next));
    int j=0;
    for(int i=2;i<=lens;++i)
    {
        while(j&&s[i]!=s[j+1]) j=next[j];
        if(s[i]==s[j+1]) ++j;
        next[i]=j;
    }
}

void dfs(int i)
{
    if(!i) return;
    ++ans;f[i]=1;
    dfs(next[i]);
}

void work()
{   
    kmp_();

    memset(d,0,sizeof(d));
    for(int i=1;i<=lens;++i) d[i]=1;
    for(int i=lens;i>=1;--i) d[next[i]]+=d[i];

    ans=0;
    memset(f,0,sizeof(f));
    dfs(lens);
    printf("%d\n",ans);
    for(int i=1;i<=lens;++i) if(f[i]) printf("%d %d\n",i,d[i]);
}

int main()
{
    scanf("%s",s+1);
    lens=strlen(s+1);
    work();
    return 0;
}

Q^Q