2019牛客暑期多校训练营（第五场） C generator 2 【BSGS算法】

本文链接：https://blog.youkuaiyun.com/henucm/article/details/99682328

本文深入探讨了解线性同余方程的方法，特别是针对形式为x[i]=(a*x[i-1]+b)%p的序列，提出了一种结合扩展欧几里德算法和BSGS算法的高效解决方案。通过分解变量n，利用hash表优化查找过程，有效解决了在特定条件下寻找满足条件的x数组下标的问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

传送门

题意：已知x[i]=(a*x[i-1]+b)%p，求满足等式的x数组的下标，且该下标小于n。若不存在则输出-1。

思路：

1.x0==v ,直接输出0

2.a==0 (1)v==x0 输出0

(2)v==b 输出1

(3)否则输出-1

3.a==1 式子就可以化简成

xn=x0+nb mod

整理得 xn-x0=nb mod p

令 z=xn-x0, x=n

bx=z mod p

即 bx+mp=z 其中b,p,z 为已知，就可以用扩张欧几里德先求bx+mp=1 的解再乘z

当然也可以除以b等于乘b的逆元再乘Z。

4. 将原式化简

我们发现第 n 项是这样的：b + ba + ba^2 + ba^3 + ... + ba^(n - 1) + x0a^n

我们等比数列求和简化一下：

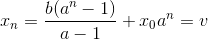
我们要解这个n，就把n当做未知数解一下：

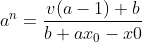
然后再用BSGS解这个方程

为了方便，我们把右边那一堆看做V。在同余的情况下，n最大不超过mod，我们把n分解为 x*t1 - t2

令t1 = 1000，t2 <= 1000，那么x最大1e6：

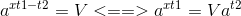
$a^{xt1-t2}=V <==>a^{xt1}=Va^{t2}$

如果只能用map可TLE 然后我们用 unordered_map(卡过) 或者用hash来优化(大概快了5倍)

/*_______________########_______________________
/*_______________#########_______________________
/*______________############_____________________
/*______________#############____________________
/*_____________##__###########___________________
/*____________###__######_#####__________________
/*____________###_#######___####_________________
/*___________###__##########_####________________
/*__________####__###########_####_______________
/*________#####___###########__#####_____________
/*_______######___###_########___#####___________
/*_______#####___###___########___######_________
/*______######___###__###########___######_______
/*_____######___####_##############__######______
/*____#######__#####################_#######_____
/*____#######__##############################____
/*___#######__######_#################_#######___
/*___#######__######_######_#########___######___
/*___#######____##__######___######_____######___
/*___#######________######____#####_____#####____
/*____######________#####_____#####_____####_____
/*_____#####________####______#####_____###______
/*______#####______;###________###______#________
/*________##_______####________####______________
/*/

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int t1 = 1001,t2 = 1e6;
struct hash{
    static const int N=1e6+10;
    static const int mod=2000000;
    int head[mod+10],hs[N],nxt[N],id[N];
    int tot;
    void init()
    {
        memset(head,-1,sizeof(head));
        tot=0;
    }
    void insert(int x,int y)
    {
        int k=x%mod;
        hs[tot]=x;
        id[tot]=y;
        nxt[tot]=head[k];
        head[k]=tot++;
    }
    ll find(ll x)
    {
        int k=x%mod;
        for(int i=head[k];i!=-1;i=nxt[i])
        {
            if(hs[i]==x)
            {
                return id[i];
            }
        }
        return -1;
    }
}hs;
ll power(ll a,ll b,ll p)
{
    ll ans=1;
    while(b)
    {
        if(b&1)
        ans=ans*a%p;
        a=a*a%p;
        b>>=1;
    }
    return ans;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        ll n,x0,a,b,p;
        scanf("%lld%lld%lld%lld%lld",&n,&x0,&a,&b,&p);
        ll s=power(a,t1,p);
        ll x=1;
        hs.init();
        for(int i=1;i<=t2;i++)
        {
            x=1ll*x*s%p;
            if(hs.find(x)==-1)
            hs.insert(x,i*t1);
        }
        ll mu=(b+1ll*a*x0%p-x0+p)%p;
        ll inv=power(mu,p-2,p);
        int q;
        scanf("%d",&q);
        while(q--)
        {
            ll v;
            scanf("%lld",&v);
            if(!a)
            {
                if(v==x0)
                printf("0\n");
                else if(v==b)
                {
                    printf("1\n");
                }
                else
                printf("-1\n");
                continue;
            }
            if(a==1)
            {
                ll ans=(v-x0+p)*power(b,p-2,p)%p;
                if(ans<n)
                printf("%lld\n",ans);
                else
                printf("-1\n",ans);
                continue;
            }
            ll ans=p+1;
            v=(v*(a-1)%p+b)*inv%p;
            ll y=v;
            for(int i=0;i<=t1;i++)
            {
                if(hs.find(y)!=-1)
                ans=min(ans,hs.find(y)-i);
                y=y*a%p;
            }
            if(ans==p+1||ans>n)
            printf("-1\n");
            else
            printf("%lld\n",ans);
        }
    }
    return 0;
}