本文介绍了数据整型的定义和在内存中的存储方式，包括原码、反码和补码的概念。接着探讨了大小端字节序，以及如何通过程序判断系统字节序。此外，还详细解析了浮点数的内存表示，遵循的IEEE标准以及不同浮点数家族类型的范围。
目录
一. 数据整型的介绍
#define MB_LEN_MAX 5
#define SHRT_MIN (-32768)
#define SHRT_MAX 32767
#define USHRT_MAX 0xffff
#define INT_MIN (-2147483647 - 1)
#define INT_MAX 2147483647
#define UINT_MAX 0xffffffff
#define LONG_MIN (-2147483647L - 1)
#define LONG_MAX 2147483647L
#define ULONG_MAX 0xffffffffUL
#define LLONG_MAX 9223372036854775807i64
#define LLONG_MIN (-9223372036854775807i64 - 1)
#define ULLONG_MAX 0xffffffffffffffffui64
二. 整形在内存中的存储
1.二进制表示形式：原码、反码、补码
三种表示方法都由符号位和数值位构成，符号位是0为正，是1为负
正数的原码、反码、补码都相同
负数
原码：符号位为1，数值位正常2进制翻译就行
反码：原码符号位不变，数值位按位取反
补码：反码+1
int num = 10;//创建一个整型变量num，这时num向内存申请4个字节来存放数据
//4个字节--32个比特位
//00000000000000000000000000001010 - 原码
//00000000000000000000000000001010 - 反码
//00000000000000000000000000001010 - 补码 int num = -10;
//10000000000000000000000000001010 - 原码
//11111111111111111111111111110101 - 反码
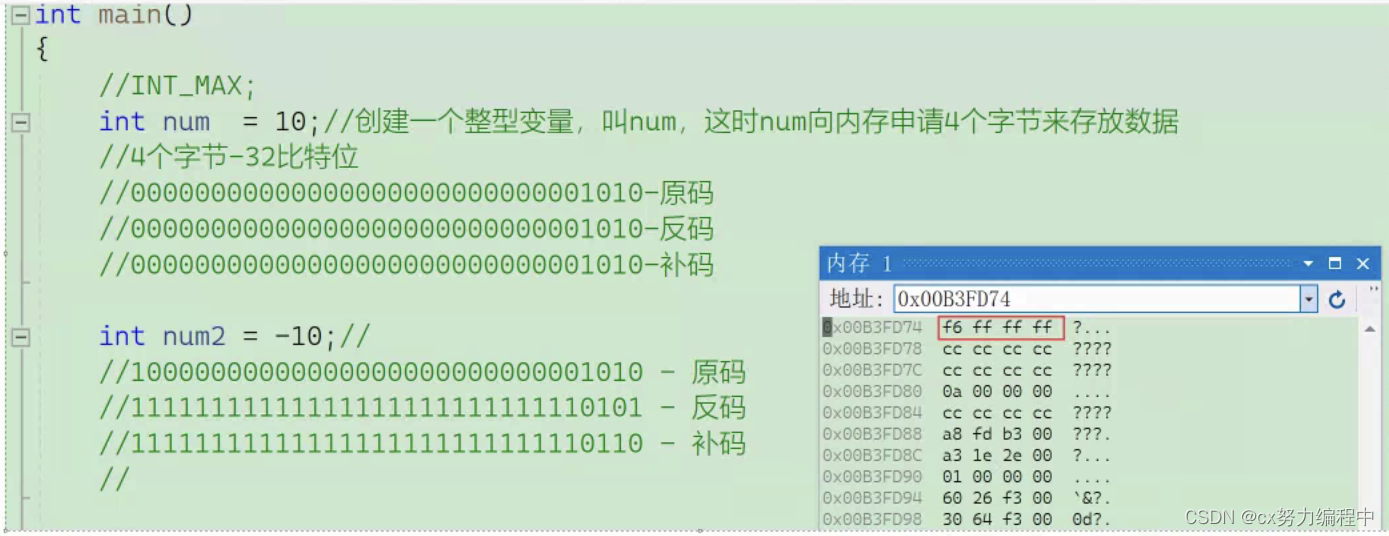
//11111111111111111111111111111110 - 补码在内存窗口查看num = 10的内存存储
本质上内存中存放的是二进制，但在VS上面为了方便展示，显示的是16进制
我们发现内存是倒着存储的
再来看看num2 = -10的存储
对于整形来说：数据存放内存中其实存放的是补码。
比如我们算1-1，也就是1+（-1）
假设用原码相加
00000000000000000000000000000001 --> 1
10000000000000000000000000000001 --> -1
相加得：10000000000000000000000000000010 -- -2
说明用原码计算是有问题的，所以采用补码
00000000000000000000000000000001 --> 1的补码
1111111111111111111111111111111111111 --> -1的补码
相加：00000000000000000000000000000000 （第一位的1溢出了，不用）
三. 大小端字节序
给你一个内存0x 11 22 33 44你会怎么存（11 是一个字节）
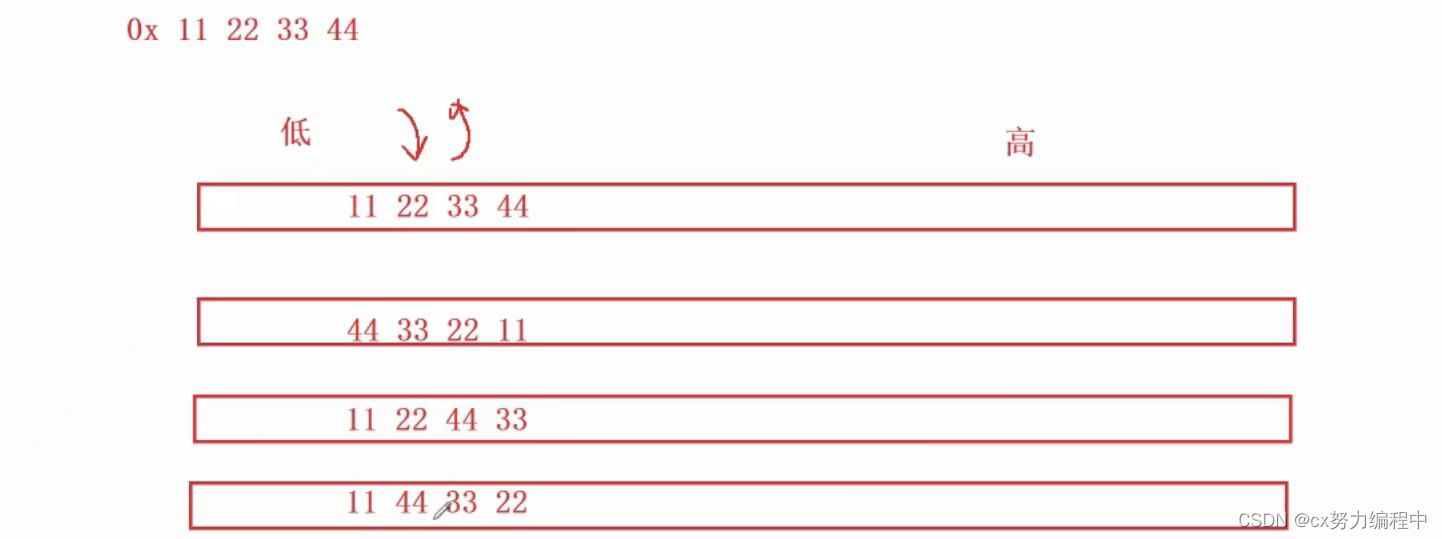
其实有很多种存储方法，但是这样的存储方式太乱了，所以内存选择了前面两种存储方式
字节序：是以字节为单位，讨论存储顺序的
44 33 22 11 小端字节序存储
把一个数据的低位字节的内容，存放在低地址处，把一个数据的高位字节的内容，存放在高地址处
11 22 33 44 大端字节序存储
把一个数据的低位字节的内容，存放在高地址处，把一个数据的高位字节的内容，存放在低地址处
写个程序来判断大小端
int a = 0;//0x 00 00 00 01
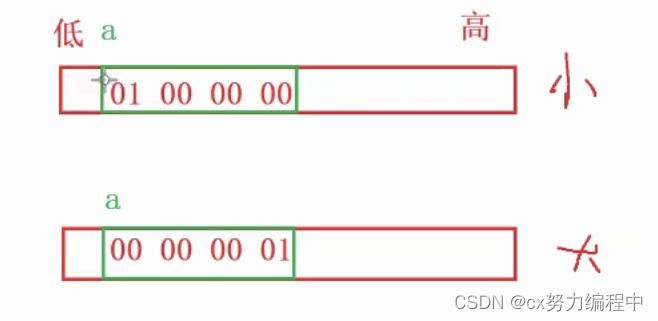
&a取出第一个字节的地址.
因为&a是int*类型，解引用访问四个字节，这可不行。所以我们使用强制类型转换成char*，再来解引用就访问一个字节了。
if (*(char*))&a == 1)这就是小端
else大端
//方式1
int main()
{
int a = 1;
char* p = (char*)&a;//int*
if (*p == 1)
printf("小端\n");
else
printf("大端\n");
return 0;
}
//方式2
int check_sys()
{
int a = 1;
if (*(char*)&a == 1)
return 1;
else
return 0;
}
//小端返回1
//大端返回0
//简化版
int check_sys()
{
int a = 1;
return *(char*)&a;
}
int main()
{
int ret = check_sys();
if(ret == 1)
printf("小端\n");
else
printf("大端\n");
return 0;
}
整型的存储
表示范围可以在limits.h里面查找
那有符号的char和无符号的char有什么区别呢？
signed char 8bit 第一位是符号位
内存范围：-128~127
unsigned char 8 bit 每一位都是数值位
内存范围：0~255
注意：由于没有符号位 unsigned char没有正负之分，纯纯数值大小
练习：
1. 打印结果？
#include <stdio.h>
int main()
{
char a = -1;
signed char b = -1;
unsigned char c = -1;
printf("a=%d,b=%d,c=%d", a, b, c);
return 0;
}分析和结果：
2.打印结果？
int main()
{
char a = -128;
printf("%u\n", a);
return 0;
}
因为整型提升部分截取的后八个比特位相同都是10000000，符号位相同，整型提升都在前面补1，所以算出来的结果128和-128都一样
3.打印结果？
int main()
{
int i = -20;
unsigned int j = 10;
printf("%d\n", i + j);
return 0;
}分析和结果
4.打印结果？
int main()
{
unsigned int i;
for (i = 9; i >= 0; i--)
{
printf("%u\n", i);
}
return 0;
}
结果：死循环，我们用Sleep函数放慢打印
发现从9降到0之后变成了4294967295
这是因为0之后的-1的补码是32位1，unsigned类型不管正负，直接把-1的补码当成原码来打印。结果就死循环了
5.打印结果？
int main()
{
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
printf("%d", strlen(a));
return 0;
}一般来说，这个a会存放-1到-1000的数字，但是因为char类型存放数据的范围是-128~127，所以只能存放-1 -2 -3...-128 127 126 125 ... 3 2 1 0 256个数字
然后再次循环存放-1 -2 -3...-128 127 126 125 ... 3 2 1 0 256个数字，
直到把1000个数字空间填满
而这里的strlen是求字符串长度的，统计的是\0之前出现的字符的个数。\0的ASCII码值是0，这就说明只打印-1到-128到1（0不能算）这255个数字。
所以结果是：255
四. 浮点数在内存的存储
浮点数：数学中的小数
1E10 = 1.0 × 10^10
浮点数家族类型在内存中的范围：float.h里面查找
可以在vs里面输入include<float.h>，按住ctrl再点击float.h就可以跳转
#define DBL_DECIMAL_DIG 17 // # of decimal digits of rounding precision
#define DBL_DIG 15 // # of decimal digits of precision
#define DBL_EPSILON 2.2204460492503131e-016 // smallest such that 1.0+DBL_EPSILON != 1.0
#define DBL_HAS_SUBNORM 1 // type does support subnormal numbers
#define DBL_MANT_DIG 53 // # of bits in mantissa
#define DBL_MAX 1.7976931348623158e+308 // max value,double max
#define DBL_MAX_10_EXP 308 // max decimal exponent
#define DBL_MAX_EXP 1024 // max binary exponent
#define DBL_MIN 2.2250738585072014e-308 // min positive value,double min
#define DBL_MIN_10_EXP (-307) // min decimal exponent
#define DBL_MIN_EXP (-1021) // min binary exponent
#define _DBL_RADIX 2 // exponent radix
#define DBL_TRUE_MIN 4.9406564584124654e-324 // min positive value
#define FLT_DECIMAL_DIG 9 // # of decimal digits of rounding precision
#define FLT_DIG 6 // # of decimal digits of precision
#define FLT_EPSILON 1.192092896e-07F // smallest such that 1.0+FLT_EPSILON != 1.0
#define FLT_HAS_SUBNORM 1 // type does support subnormal numbers
#define FLT_GUARD 0
#define FLT_MANT_DIG 24 // # of bits in mantissa
#define FLT_MAX 3.402823466e+38F // max value,float max
#define FLT_MAX_10_EXP 38 // max decimal exponent
#define FLT_MAX_EXP 128 // max binary exponent
#define FLT_MIN 1.175494351e-38F // min normalized positive value
#define FLT_MIN_10_EXP (-37) // min decimal exponent
#define FLT_MIN_EXP (-125) // min binary exponent
#define FLT_NORMALIZE 0
#define FLT_RADIX 2 // exponent radix
#define FLT_TRUE_MIN 1.401298464e-45F // min positive value
#define LDBL_DIG DBL_DIG // # of decimal digits of precision
#define LDBL_EPSILON DBL_EPSILON // smallest such that 1.0+LDBL_EPSILON != 1.0
#define LDBL_HAS_SUBNORM DBL_HAS_SUBNORM // type does support subnormal numbers
#define LDBL_MANT_DIG DBL_MANT_DIG // # of bits in mantissa
#define LDBL_MAX DBL_MAX // max value
#define LDBL_MAX_10_EXP DBL_MAX_10_EXP // max decimal exponent
#define LDBL_MAX_EXP DBL_MAX_EXP // max binary exponent
#define LDBL_MIN DBL_MIN // min normalized positive value
#define LDBL_MIN_10_EXP DBL_MIN_10_EXP // min decimal exponent
#define LDBL_MIN_EXP DBL_MIN_EXP // min binary exponent
#define _LDBL_RADIX _DBL_RADIX // exponent radix
#define LDBL_TRUE_MIN DBL_TRUE_MIN // min positive value
#define DECIMAL_DIG DBL_DECIMAL_DIG现在拿一道题目来引入
#include<stdio.h>
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
*pFloat = 9.0;
printf("n的值为:%d\n", n);
printf("*pFloat的值为：%f\n", *pFloat);
return 0;
}一开始我上来直接这么分析，n = 9，那第一个n等于9没问题，pFloat改成浮点类型大一出来就是9.00000，pFloat改成9.0，那n整型不变打印出来还是9，pFloat也就是9.00000
当我一打印我就傻眼了
第二个值和第三个值不一样
这是因为整型和浮点型在内存中的存储方式有差异
根据IEEE的存储规定，任意一个二进制浮点数V可以表示成(-1)^S*M*2^E
(-1)^S表示符号位，S=0，V为正数；S=1，V为负数
M是[1,2)之间的有效数字
2^E是指数位
举例：
5.5-10进制的浮点数转成2进制101.1
再写成科学计数法：1.011*2^2
V=5.5=(-1)^0*1.011*2^2
S = 0; M = 1.011; E = 2
特别规定：
（1）M经过移位之后变成1.xxxxxxx的类型，规定存储M时，默认这个数第一位总是1，因此舍去，只保留后面的xxxxx小数位，这样可以提高精度
（2）E是一个无符号整数，为了防止负数对存储的影响，存入E的真实值必须加上一个中间数，对于8位的E，中间数是127；对于11位的E（double类型），中间值是1023.也就是说，在存储E的时候要加上这个中间数，如2^-1中E为-1，那存储E的时候就是-1+127 = 126（正数E也要加）
（3）E从内存中取出分为三种情况：
a.E不全为0或不全为1
E的计算值减去127（或1023)，得到真实值，再将有效数字M前加上第一位的1
b.E全为0
指数E等于1-127（或1-1023），有效数字M不再加上第一位的1，而是还原成0.xxxxxx的小数。（表示±0和接近于0的很小的数字）
c.E全为1
有效数字M为0，表示±∞
回到上面的代码，先看上半部分（未修改值前）
第一个n，以整数形式存储和取出，值不变9
计算第二个值
n = 9，写成二进制形式是000000000000000000000000000000001001
用浮点数存储的时候0 00000000 00000000000000000000001001
S E M
E在内存中是全0，所以取出时E = -126, M = 0.0000000000000000000001001
V = （-1）^ 0 * 0.0000000000000000000001001 * 2 ^ -126，这个数接近于0，所以第二个值打印出来只能是0.00000000
接下来看下半部分
9.0 = 1001.0 = 1.001 * 2 ^ 3
存储：(-1)^0*1.001*2^3 S = 0, E = 3, M = 1.001
取出：S = 0, E = 3+127 = 130 = 10000010, M = 001000000000000000000000
01000001000100000000000000000000,n的打印是这段二进制序列（补码）的原码
转换之后n = 1091567616
至于下面的pFloat，因为是浮点数形式存储和取出，所以值是不变的9.0
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
