目录:
1. 冒泡排序
2. 选择排序
3. 插入排序
4. 希尔排序
5. 归并排序
6. 快速排序
1.冒泡排序
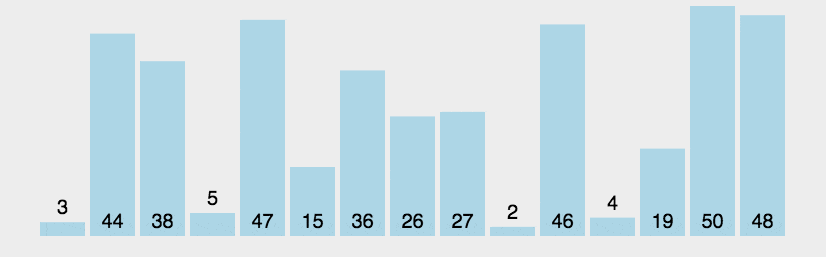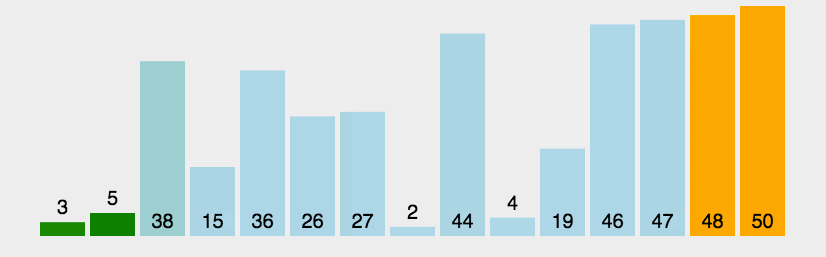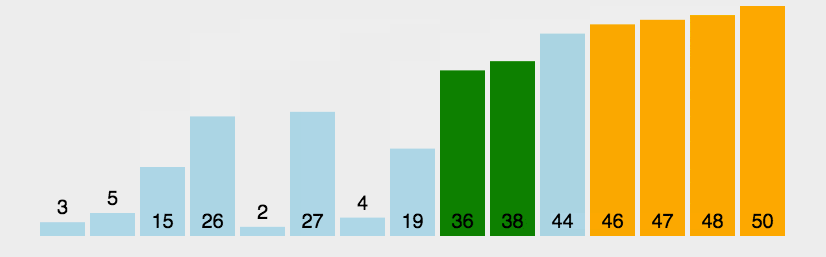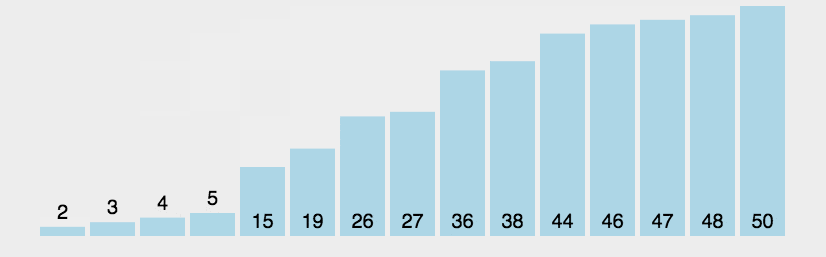
冒泡排序需要遍历列表

如上图所示,第一轮遍历列表时,我们发现较大的数被放在前面,显然不合顺序(从大到小),我们两个元素两个元素遍历,比较两个数,发现大的就往后排,小的就往前面排 。如果列表中有n个元素,那么第一轮遍历就要比较n-1对元素
第二轮遍历的时候,最大值已经在正确位置上了,还剩n-1个元素需要排列,再遍历交换下去,一直到排序完毕。
给出一段python小代码
#冒泡排序
def bubblesort(alist):
for passnum in range(len(alist) - 1):
for i in range(passnum):
if alist[i]>alist[i+1]:
temp = alist[i]
alist[i] = alist[i+1]
alist[i+1] = temp
我们发现,这段代码的时间复杂度时O(n^2),容易超时,所以我们要对代码进行修改
#冒泡排序(改进后)
def shortbubblesort(alist):
exchanges = True
passnum = len(alist) - 1
while passnum > 0 and exchanges:
exchanges = False
for i in range(passnum):
if alist[i] > alist[i+1]:
exchanges = True
alist[i+1], alist[i] = alist[i], alist[i+1]
passnum = passnum -1
2. 选择排序
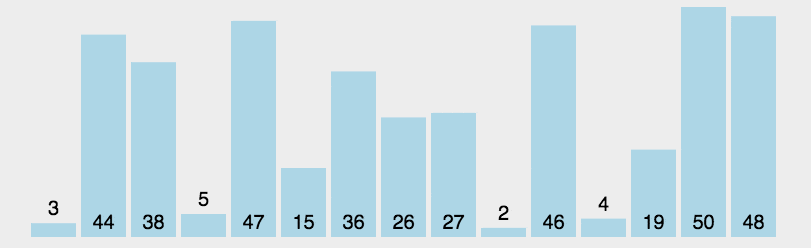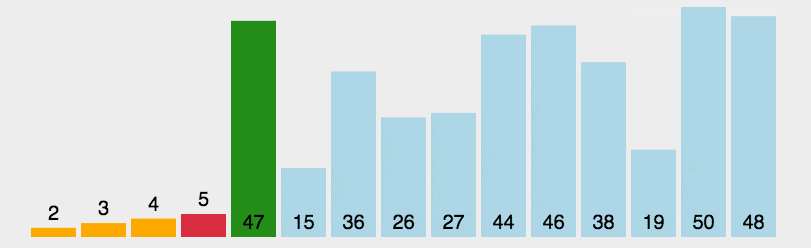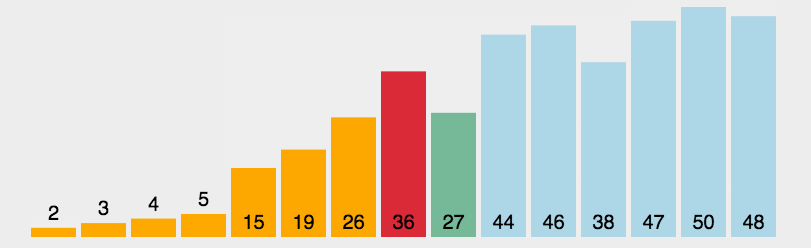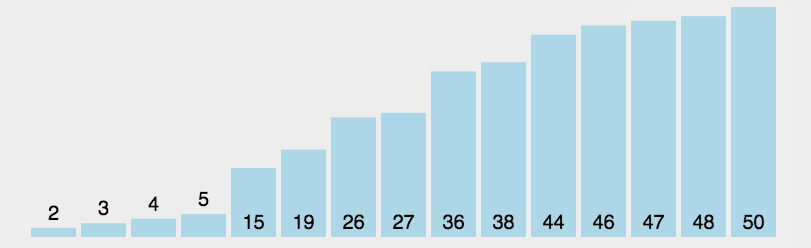
选择排序在冒泡排序的基础上进行了改进,每次遍历列表只进行一次交换,就是找出列表里还未排序的数中的最大值,把它扔到后面去

如上图所示
python代码
#选择排序
def selectionsort(alist):
for i in range(len(alist)-1, 0, -1):
max = 0
for j in range(1, i+1):
if alist[j] > alist[max]: #把最大值往后面放
max = j
alist[i], alist[max] = alist[max], alist[i]
3.插入排序
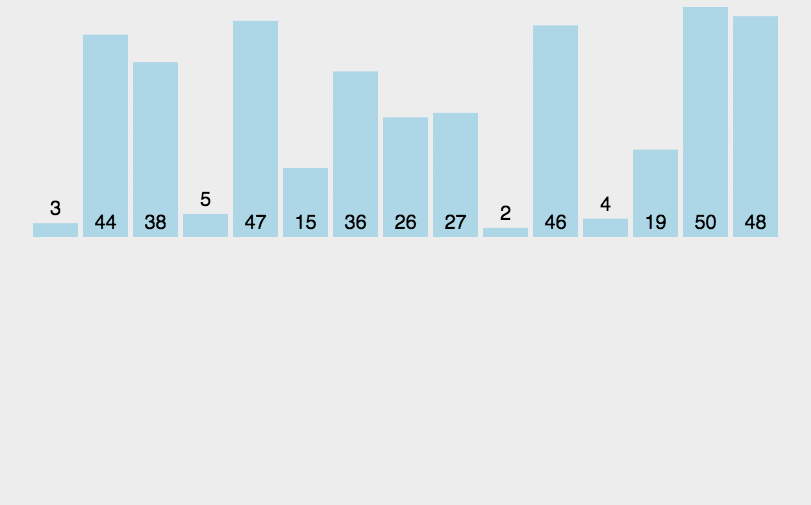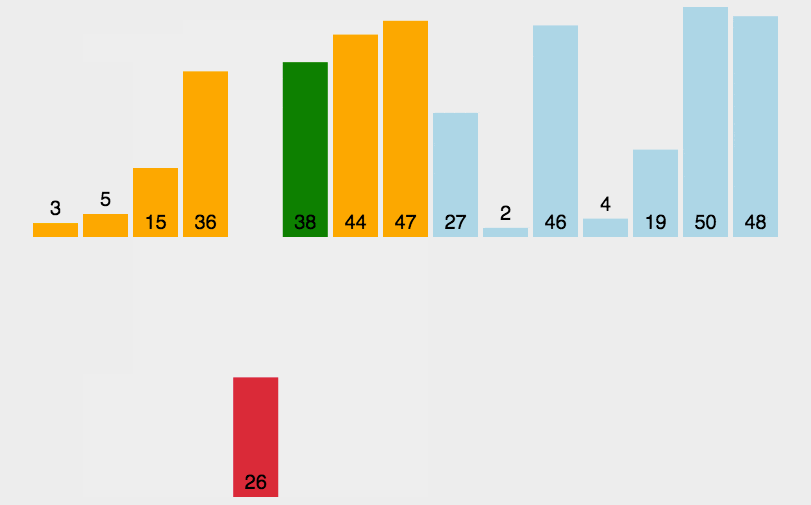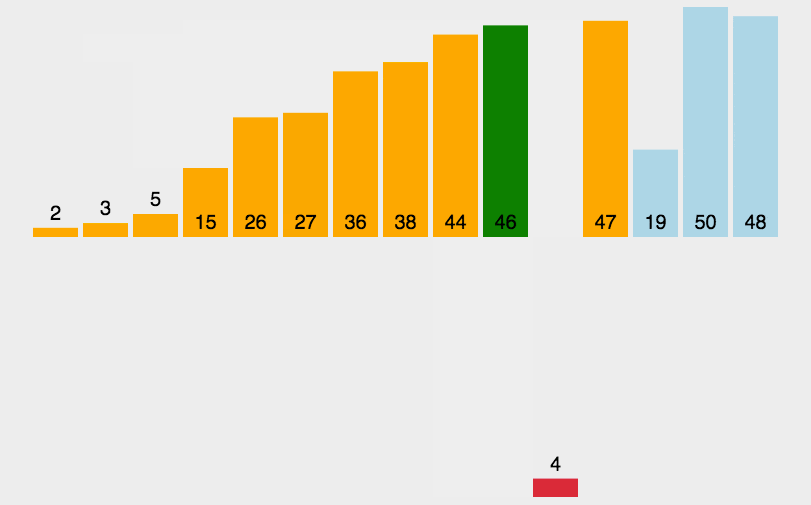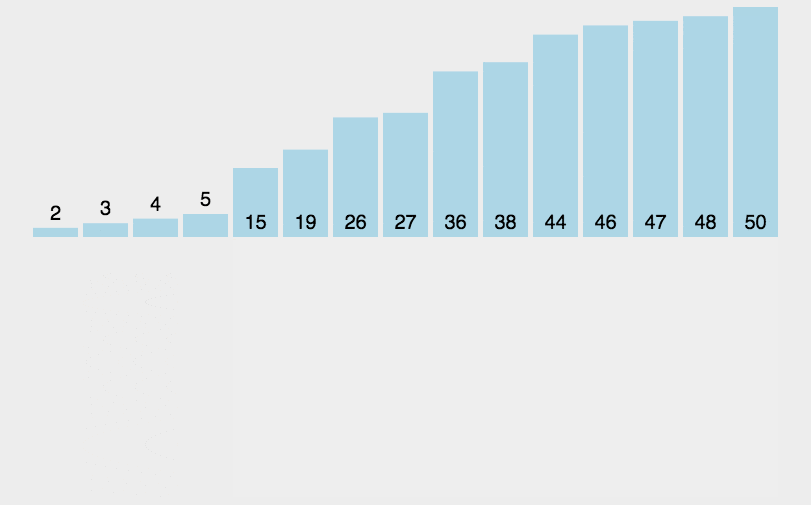
插入排序是先将位置0的元素当作单元素的有序子列表,从第一个元素到第n-1个元素,每一轮都将当前元素与上面这个单元素的有序子列表进行比较,小的往前排,大的往后排。插入后,列表扩展,下一个元素再与这两个元素进行比较。

python代码
#插入排序
def insertsort(alist):
for i in range(len(alist)):
num = alist[i]
position = i
while position>1 and alist[position-1]>num:
alist[position] = alist[position - 1]
position -= 1
alist[position] = num
4. 希尔排序、
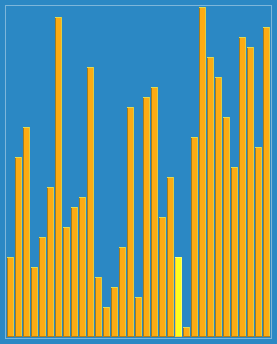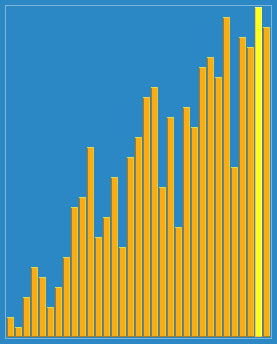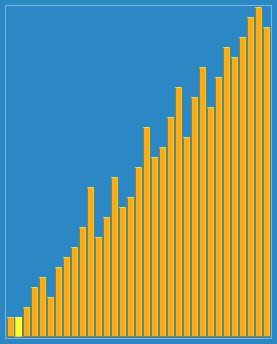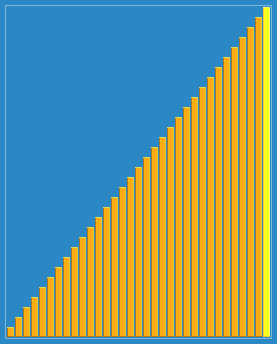

将排序好的子列表中的元素一一往下放

最后将填充完元素的列表进行再一次排序

#希尔排序
def shellsort(alist):
sublen = len(alist) // 2 #子列表长度
while sublen > 0:
for start in range(sublen):
gapinsertion(alist, start, sublen)
print("经过增量为", sublen, "后,这个列表是", alist)
sublen = sublen // 2
def gapinsertion(alist, sta, gap):
for i in range(sta + gap, len(alist), gap):
cvalue = alist[i]
pos = i #将当前值的位置设置为i
while pos >= gap and alist[pos - gap]>cvalue: #循环直到当前值再子列表的正确位置上
alist[pos] = alist[pos - gap] #把当前位置的元素向右移动
pos = pos - gap
alist[pos] = cvalue
alist = [54, 26, 93, 17, 77, 31, 44, 55]
shellsort(alist)
这段代码的结果为

5. 归并排序
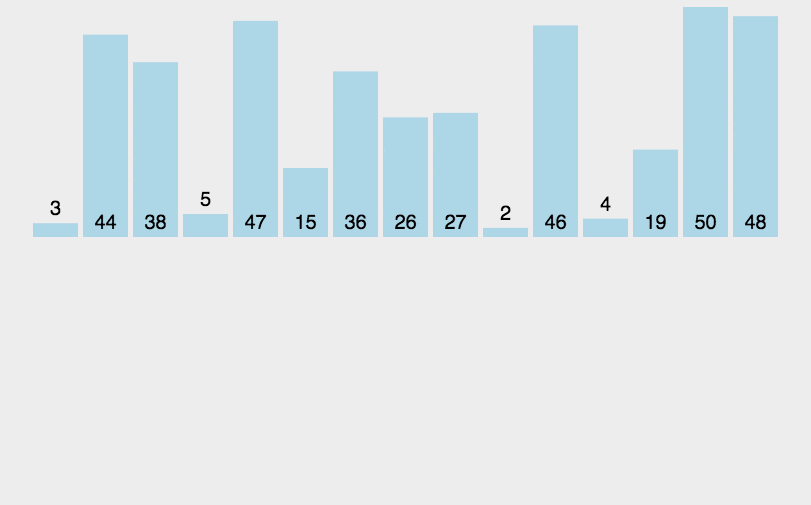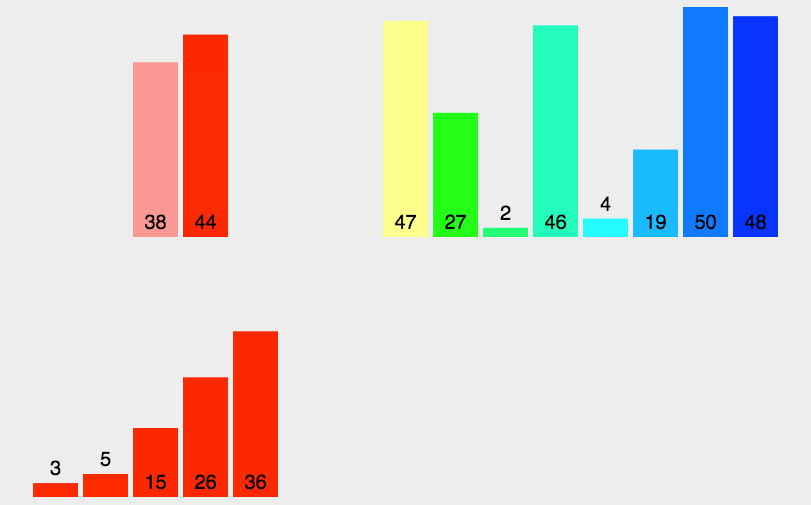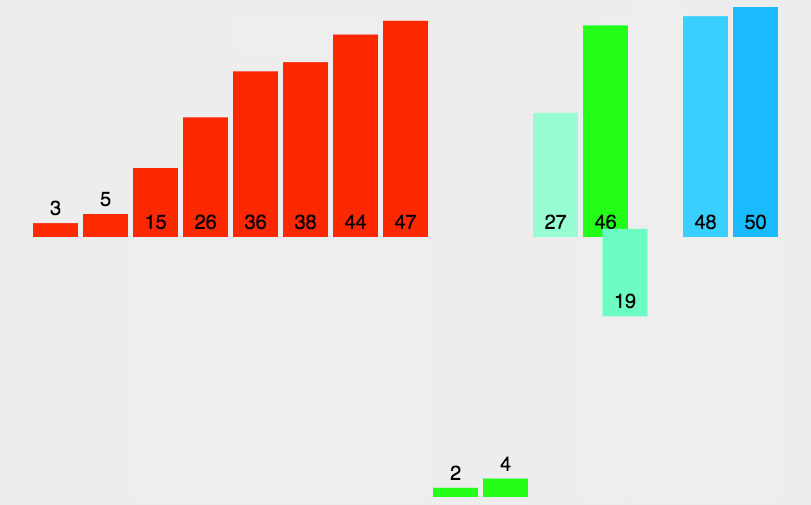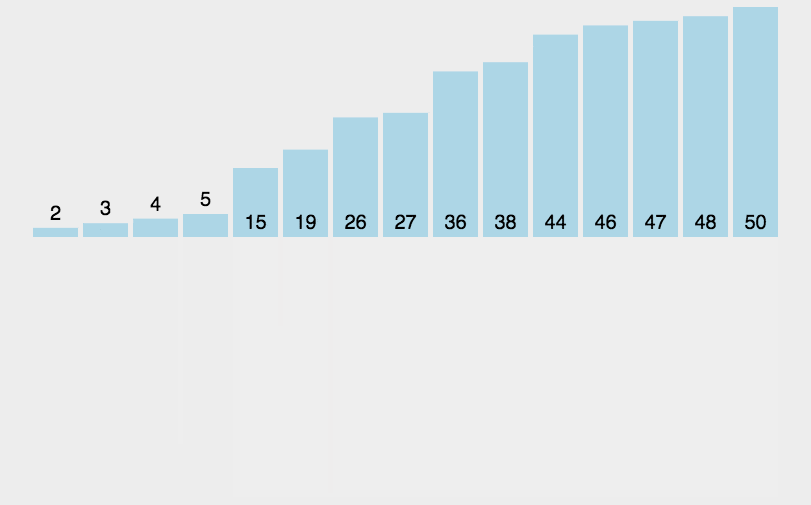
归并排序本质上是一种递归算法,每次将一个列表一分为二,如果列表为空或者只有一个元素,那默认为有序,如果有两个及以上元素的话,先将列表一分为二,对两部分进行递归调用归并排序,等所有排序完成时,把这些元素一一合并就🆗了

python代码
#归并排序
def mergesort(alist):
print("二分", alist) # 打印当前二分的列表
if len(alist) > 1:
mid = len(alist) // 2 # 计算中间索引位置
left = alist[:mid] # 分割左半边列表
right = alist[mid:] # 分割右半边列表
mergesort(left) # 递归调用归并排序函数对左半边进行排序
mergesort(right) # 递归调用归并排序函数对右半边进行排序
i = 0
j = 0
k = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
alist[k] = left[i] # 如果左半边元素小于右半边元素,将左半边的元素放到合并后的列表中
i = i+1
else:
alist[k] = right[j] # 如果右半边元素小于左半边元素,将右半边的元素放到合并后的列表中
j = j+1
k = k+1
while i < len(left):
alist[k] = left[i] # 如果左半边还有元素没有加入到合并后的列表中,直接将它们加入到列表中
i = i + 1
k = k + 1
while j < len(right):
alist[k] = right[j] # 如果右半边还有元素没有加入到合并后的列表中,直接将它们加入到列表中
j = j + 1
k = k + 1
print("merging ", alist) # 打印当前合并后的列表
b = [14, 23, 56, 97, 100, 89, 45, 67]
mergesort(b)
输出结果为
二分 [14, 23, 56, 97, 100, 89, 45, 67]
二分 [14, 23, 56, 97]
二分 [14, 23]
二分 [14]
merging [14]
二分 [23]
merging [23]
merging [14, 23]
二分 [56, 97]
二分 [56]
merging [56]
二分 [97]
merging [97]
merging [56, 97]
merging [14, 23, 56, 97]
二分 [100, 89, 45, 67]
二分 [100, 89]
二分 [100]
merging [100]
二分 [89]
merging [89]
merging [89, 100]
二分 [45, 67]
二分 [45]
merging [45]
二分 [67]
merging [67]
merging [45, 67]
merging [45, 67, 89, 100]
merging [14, 23, 45, 56, 67, 89, 97, 100]
6. 快速排序
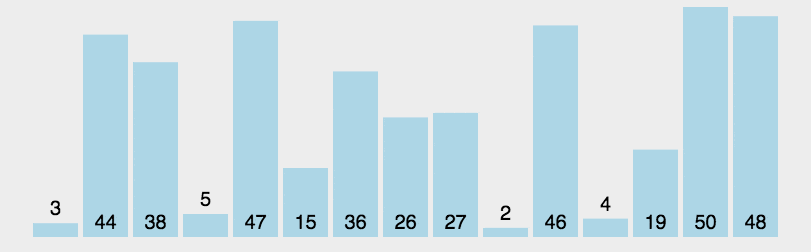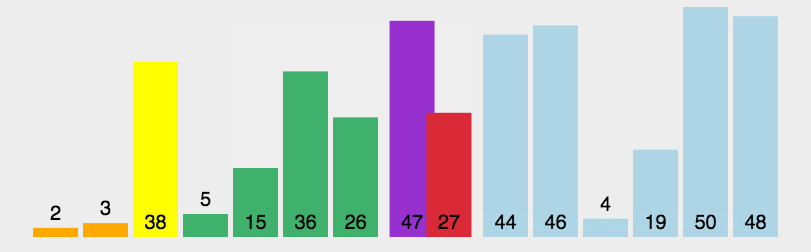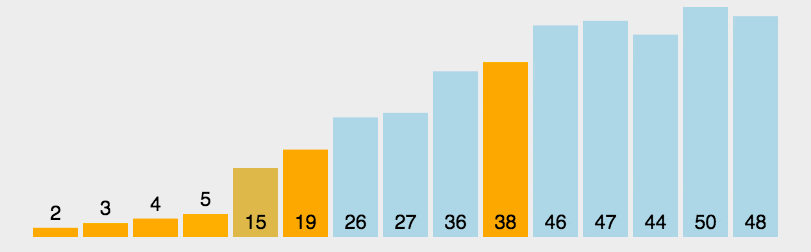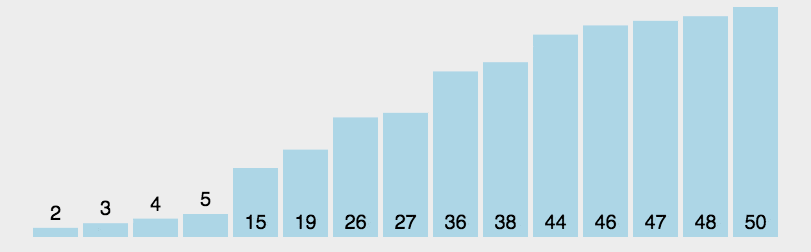
快速排序首先需要选出一个基准值,基准值的作用是帮助切分列表,基准值的位置也叫做分割点。
接着进行划分操作,比基准值大的放右边,比基准值小的放左边
在本例中,我们选取54作为第一个基准值


python代码
# 定义快速排序函数
def quicksort(alist):
# 调用快速排序辅助函数
quicksortHelper(alist, 0, len(alist) - 1)
# 定义快速排序辅助函数
def quicksortHelper(alist, first, last):
# 判断是否需要排序
if first < last:
# 将列表分为两部分
splitpoint = partition(alist, first, last)
# 对左侧子列表进行快速排序
quicksortHelper(alist, first, splitpoint - 1)
# 对右侧子列表进行快速排序
quicksortHelper(alist, splitpoint + 1, last)
# 定义分区函数
def partition(alist, first, last):
# 选择第一个元素作为基准值
pivotvalue = alist[first]
# 初始化左侧和右侧子列表的边界
leftmark = first + 1
rightmark = last
# 标记是否完成排序
done = False
# 开始排序
while not done:
# 找到左侧子列表中大于基准值的元素
while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
leftmark = leftmark + 1
# 找到右侧子列表中小于基准值的元素
while alist[rightmark] >= pivotvalue and rightmark >= leftmark:
rightmark = rightmark - 1
# 判断是否完成分区
if rightmark < leftmark:
done = True
else:
# 交换左侧子列表中大于基准值的元素和右侧子列表中小于基准值的元素
alist[leftmark], alist[rightmark] = alist[rightmark], alist[leftmark]
# 将基准值放到分区的位置,并返回分区的位置
alist[first], alist[rightmark] = alist[rightmark], alist[first]
return rightmark





















 1234
1234

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








