圆内接四边形是一种特殊的四边形,其所有顶点都位于圆的圆周上。换句话说,如果你画一个四边形,然后找到一个经过该四边形所有四个顶点的圆,那么这个四边形就称为圆内接四边形。
圆内接四边形有几个有趣的性质,例如它们的对角关系、对角线关系以及托勒密定理。本文将全面介绍圆内接四边形及其性质。
圆内接四边形定义
圆内接四边形是指内接于圆的四边形,即有一个圆通过该四边形的所有四个顶点。
圆内接四边形的顶点共圆。圆心称为外接圆心,圆半径称为外接圆半径。
如下图所示,ABCD 是一个圆内接四边形,边长分别为 a、b、c 和 d。

圆内接四边形的角
圆内接四边形的对角和互为补角。
对于圆内接四边形,设内角为∠A、∠B、∠C、∠D,则
- ∠A + ∠C = 180°...(1)
- ∠B + ∠D = 180°...(2)
将公式 (1) 和 (2) 相加,可得
∠A + ∠B + ∠C + ∠D= 360°
因此,四边形的角和性质也适用于圆内接四边形。
圆内接四边形的性质
圆内接四边形是一种特殊的四边形,其所有顶点都位于圆的圆周上。圆内接四边形的一些重要性质如下:
| 性质 | 描述 |
|---|---|
| 对角和 | 对角的度数之和始终为 180 度。 |
| 邻角和 | 圆内接四边形的邻角和始终为 180 度。 |
| 外角和 | 圆内接四边形一条边的延长角等于其内对角。 |
| 对角线 | 对角线长度的乘积等于对边乘积之和。 |
| 对角 | 任何圆内接四边形的对角都是互补的。 |
| 相等对角角平分线 | 如果圆内接四边形中的两个对角被对角线平分,那么平分线的交点位于外接圆上。 |
| 边的垂直平分线 | 圆内接四边形各边的垂直平分线交于四边形外接圆上的一点。 |
| 边的平方和 | 边的平方和等于对角线的平方和加上外接圆半径的平方的四倍。 |
| Property | Description |
|---|---|
| Sum of Opposite Angles | The sum of the measures of opposite angles is always 180 degrees. |
| Sum of Adjacent Angles | The sum of adjacent angles in a cyclic quadrilateral is always 180 degrees. |
| Exterior Angle Sum | The exterior angle formed by extending one side of the cyclic quadrilateral equals the interior opposite angle. |
| Diagonals | The product of the lengths of the diagonals equals the sum of the products of opposite sides. |
| Opposite Angles | Opposite angles of any cyclic quadrilateral are supplementary. |
| Equal Opposite Angles Bisectors | If two opposite angles in a cyclic quadrilateral are bisected by the diagonal, then the point of intersection of the bisectors lies on the circumcircle. |
| Perpendicular Bisectors of Sides | The perpendicular bisectors of the sides of a cyclic quadrilateral intersect at a point that lies on the circumcircle of the quadrilateral. |
| Sum of Squares of Sides | The sum of the squares of the sides equals the sum of the squares of the diagonals plus four times the square of the radius of the circumcircle. |
圆内接四边形公式
对于圆内接四边形有多种公式,其中一些重要的公式如下:
- 圆内接四边形的面积
- 外接圆半径
- 圆内接四边形的对角线
下面我们来详细讨论一下这些公式:
圆内接四边形面积公式
圆内接四边形的面积使用以下公式计算:
圆内四边形面积 = √(sa)(sb)(sc)(sd)
在哪里,
- a、b、c、d 是圆内接四边形的边,并且
- s是半周长 [ s = (a + b + c + d) / 2 ]。
注意:此公式也称为 Brahmagupta 公式。
外接圆半径
设圆内接四边形的边为a、b、c和d,s为半周长,则外接圆半径为,

圆内接四边形的对角线
对角线是任何多边形中连接任意两个不相邻顶点的线。
假设 a、b、c 和 d 是圆内接四边形的边,p 和 q 是其对角线,那么我们可以使用以下公式找到它的对角线:
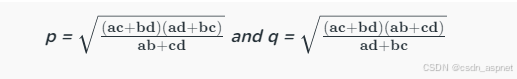
圆周四边形定理
为了更好地理解圆周四边形,我们来看一下几何学中的一些不同定理。其中一些重要的定理是:
- 内接角定理
- 托勒密定理
现在,让我们详细研究这些定理:
内接角定理
根据内接角定理,
任何圆内接四边形的对角和都是补角。
已知:一个圆内接四边形 ABCD,位于以 O 为圆心的圆内。
构造:连接半径 OA 和 OC
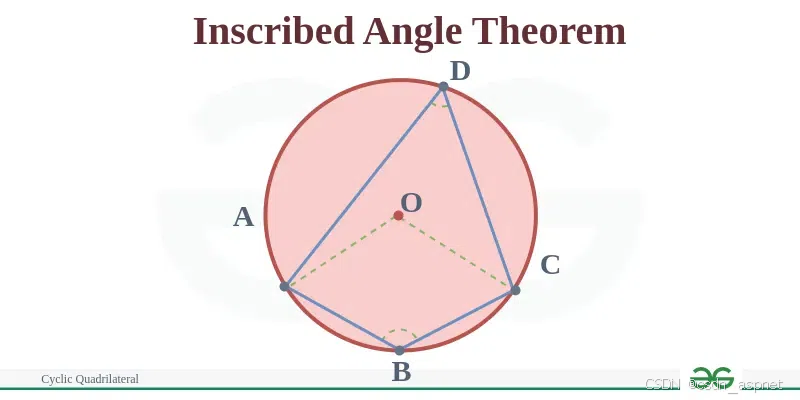
证明: 在四边形ABCD中,
2 × ∠ABC = 反射 ∠ AOC(根据圆周定理)...(等式 1)
相似地,
2 × ∠ADC = ∠ AOC...(等式 2)
我们知道,
∠ AOC + 反射 ∠ AOC = 360°...(等式 3)
根据方程(1)+方程(2)
2 × ∠ADC + 2 × ∠ABC = 反射 ∠ AOC + ∠ AOC
2 × (∠ADC + ∠ABC) = 反射∠AOC + ∠AOC
2 × ∠ADC + ∠ABC = 360°(根据等式 3)
∠ADC + ∠ABC = 180°(补充)
相似地,
∠BAD + ∠BCD = 180°(补充)
因此,圆内接四边形的对角互补。
上述定理的逆命题也成立。
即,如果四边形的对角和互补,那么它就是圆内接四边形。
托勒密定理
托勒密定理以希腊天文学家和数学家克劳狄斯·托勒密(约公元100年 - 约公元170年)的名字命名。该定理指出:
对于任何圆内接四边形,其两对相对边的乘积之和等于其对角线的乘积。
从数学上讲,如果ABCD是一个圆内接四边形,其边为AB、BC、CD和DA,对角线为AC和BD,则托勒密定理可以表示为:
AB · CD + BC · DA = AC · BD
或者
设a、b、c、d为圆内接四边形的边长,e、f为对角线长度,则:
ac + bd = ef
结论
总而言之,圆内接四边形是指四个顶点位于一个圆上的四边形。它们具有一些特殊的性质,例如内部存在垂直线以及托勒密定理。它们很容易制作,并且有助于解决几何问题。学习圆内接四边形有助于我们更好地理解形状,并领悟数学的美妙,从而激励我们学习更多。
阅读更多,
圆内接四边形的解题示例
例 1:计算边长分别为 21 米、35 米、62 米、12 米的圆内接四边形的面积。
解决方案:
已知:a = 21 米,b = 35 米,c = 62 米,d = 12 米。
s = (a + b + c + d) / 2
∴s = (21 + 35 + 62 + 12) / 2
∴s = 65 米
自从,
k = √(s - a)(s - b)(s - c)(s - d)
∴k = √(65 - 21)(65 - 35)(65 - 62)(65 - 12)
∴k=√44×30×3×53
∴k=√209880
∴k = 458.12米²
例 2:一个四边形板球场,边长分别为 23 米、54 米、13 米和 51 米,与一个圆形草地的边界相接。如何计算这个四边形球场的面积?
解决方案:
已知:a = 23 米,b = 54 米,c = 13 米,d = 51 米。
s = (a + b + c + d) / 2
∴s = (23 + 54 + 13 + 51) / 2
∴s = 70.5 米
自从,
k = √(s - a)(s - b)(s - c)(s - d)
∴k = √(70.5 - 23)(70.5 - 54)(70.5 - 13)(70.5 - 51)
∴k = √47.5 × 16.5 × 57.5 × 19.5
∴k=√878779.68
∴k = 937.43米²
例 3:一个圆内接四边形的边长分别为 28 米、61 米、37 米、10 米,求它的面积。
解决方案:
已知:a = 23 米,b = 54 米,c = 13 米,d = 51 米。
s = (a + b + c + d) / 2
∴s = (28 + 61 + 37 + 10) / 2
∴s = 68 米
自从,
k = √(s - a)(s - b)(s - c)(s - d)
∴k = √(68 - 28)(68 - 61)(68 - 37)(68 - 10)
∴k=√40×7×31×58
∴k=√503440
∴k = 709.53 米²
例 4:如何计算边长分别为 12 厘米、21 厘米、10 厘米和 5 厘米的圆内接四边形的周长?
解决方案:
已知:a = 12 厘米,b = 21 厘米,c = 10 厘米,d = 5 厘米。
s = (a + b + c + d) / 2
∴s = (12 + 21 + 10 + 5) / 2
∴s = 24 厘米
圆内接四边形的周长 = 2s
∴圆内接四边形的周长 = 2 × 24
∴圆内接四边形的周长 = 48 厘米
例 5:求圆内接四边形中∠C 为 70° 时∠A 的值。
解决方案:
对于圆内接四边形ABCD,两个对角的和为180°。
∠A + ∠C = 180°
70° + ∠C = 180°
∠C = 180° – 70°
∠C = 110°
角C的值为120°。
例 6:ABCD 是一个圆内接四边形,边为 a、b、c 和 d,对角线为 p 和 q,那么如何计算对角线的长度?
解决方案:
对于边为 a、b、c 和 d 的圆内接四边形 ABCD,对角线长度为:
使用这些公式我们可以轻松计算对角线的长度。
参考:What is Cyclic Quadrilateral - GeeksforGeeks
如果您喜欢此文章,请收藏、点赞、评论,谢谢,祝您快乐每一天。




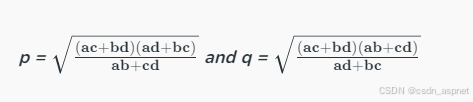


















 1521
1521

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










