四边形的构造

有句名言：几何学看似由人类创造，但其意义却完全独立于人类。实用几何是几何学的一个重要分支，它帮助我们研究物体的大小、位置、形状和维度，并用现有的几何工具绘制它们。几何学帮助我们决定使用什么材料、进行什么设计，并且在建筑过程中也发挥着至关重要的作用。不同的房屋和建筑物被建造成不同的几何形状，以赋予其新的外观，并提供适当的室内通风。简而言之，几何学是数学的一个分支，研究事物的大小、形状、位置、角度和维度。正方形、圆形和三角形等平面形状属于平面几何，被称为二维形状。这些形状只有两个维度：长度和宽度。确定几何设计通常使用四种重要的几何工具：圆规、直尺、量角器和直尺。

• 指南针——有助于绘制不同的角度。
• 直尺——它有两个三角板，用于绘制对称线。
• 量角器——用于确定和绘制正确且准确的角度。
• 尺子——用于测量和绘制线条来构建图形。

四边形

四边形是几何学中具有四条边和四个顶点的封闭多边形。四边形的其他名称包括四边形、四边形和四边形。换句话说，任何四边形都称为四边形。在本文中，我们将学习一些不同类型的四边形以及如何使用简单的几何工具构造它们。“Quad”表示“四”，“lateral”表示四边形的边。因此，所有具有四条边的封闭图形都称为四边形。任何四边形的边可以相等、不等、平行或不规则，这构成了这些四边形中各种形状的基础。无论是哪种形状，每个四边形都有四条边、四个顶点，并且所有角的总和为 360°。这适用于所有四边形。

最常见的四边形类型是正方形和长方形。我们从小学开始就学习这些基本的四边形，但在本章的这一部分，我们将介绍各种其他类型的四边形，它们具有正方形或长方形的性质，但并未被正式命名。四边形有很多不同的类型，本文将介绍其中一些。    

将构造以下类型的四边形：

• 如果给定四边形的四条边和一条对角线。
• 如果给定四边形的两条对角线和三条边。
• 如果给定四边形的两条相邻边和三个角。
• 假设给定四边形的三条边和两个夹角。
• 如果已知四边形的其他特殊性质。

让我们逐一讨论这些结构。

如果给定四边形的四条边和一条对角线：

按照以下步骤绘制四边形：

构造一个四边形 PQRS，其中 PQ= 5 厘米、QR = 7 厘米、RS = 6 厘米、PS = 6.5 厘米和 PR = 8 厘米。

首先绘制一个草图以供参考。然后按照以下步骤操作：

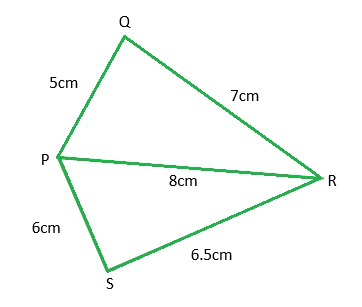
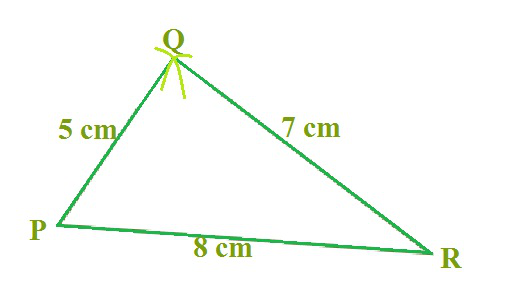
步骤1：从草图可以看出，∆PQR 可以利用 SSS 构造条件来构造。绘制 ∆PQR。

步骤2：接下来，我们需要找到第四个点S。它位于Q点相对于PR点的对侧。为此，我们进行了两次测量。

S 距离点 P 为 6 厘米。因此，以 P 为中心绘制一个半径为 6 厘米的圆弧。

步骤3： S距离R 6.5厘米。因此，以R为圆心，画一个半径为6.5厘米的圆弧

步骤4： S位于两圆弧的交点上。标记S，完成PQRS。PQRS即为所需四边形。

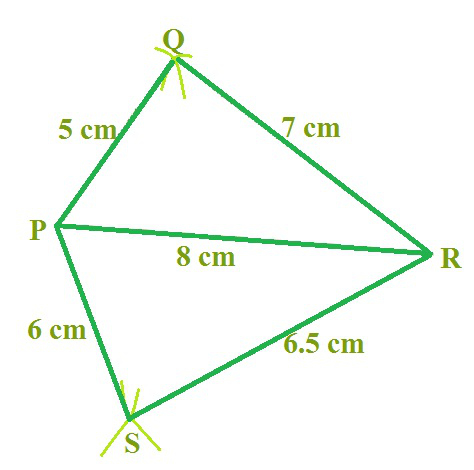
示例问题：构造四边形 ABCD，给定以下内容

AB = 4.5 厘米、BC = 5.5 厘米、CD = 4 厘米、AD = 6 厘米、AC = 7 厘米

回答： 

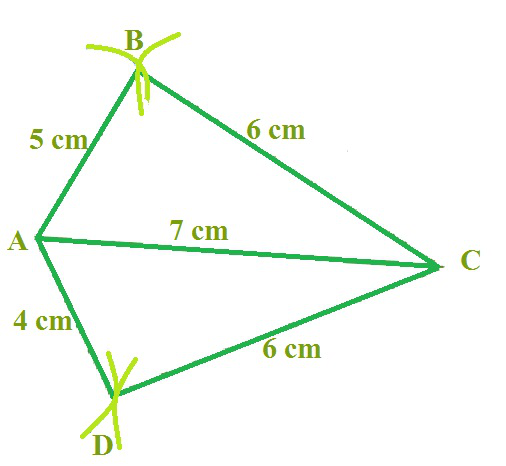
我们按照上述步骤制作四边形 ABCD，其中

AB = 5 厘米，BC = 6 厘米，CD = 6 厘米，AD = 4 厘米，AC = 7 厘米

因此，我们得到如下所示的最终结果，

因此，ABCD 就是所需的四边形。

如果给定四边形的两条对角线和三条边：

按照以下步骤绘制四边形：

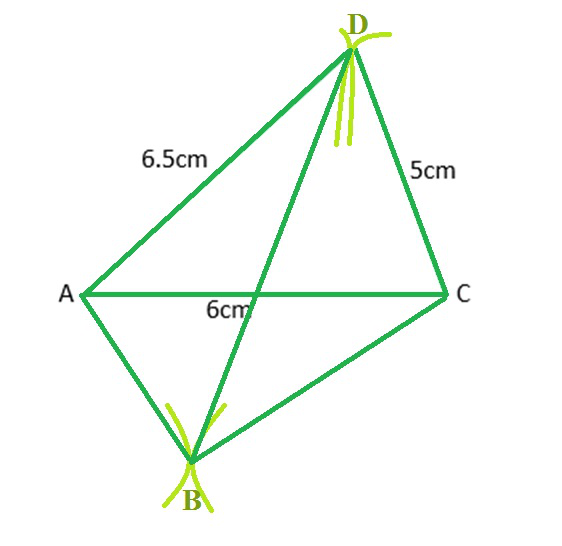
构造四边形 ABCD，已知 BC = 5.5 厘米，AD = 6.5 厘米，CD = 5 厘米，对角线 AC = 6 厘米，对角线 BD = 8 厘米。

首先，画出四边形ABCD的草图。

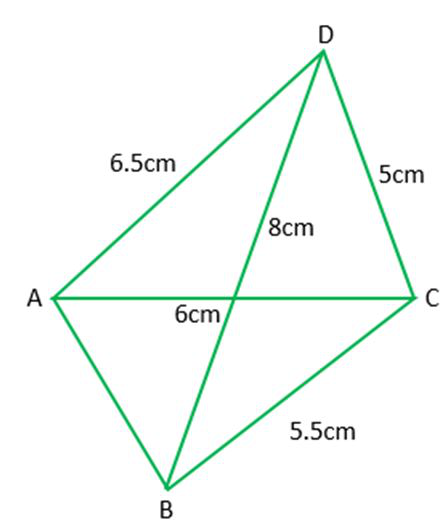
步骤 1：使用 SSS 构造绘制 ∆ACD。

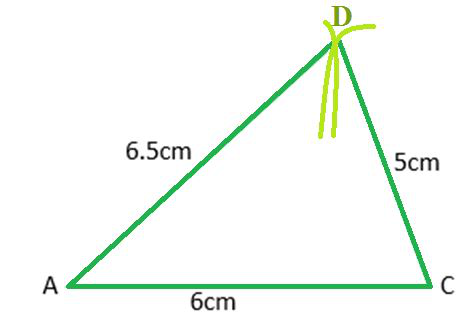
第二步：以D点为圆心，画一个半径为7厘米的圆弧。以C点为圆心，画一个半径为4.5厘米的圆弧。

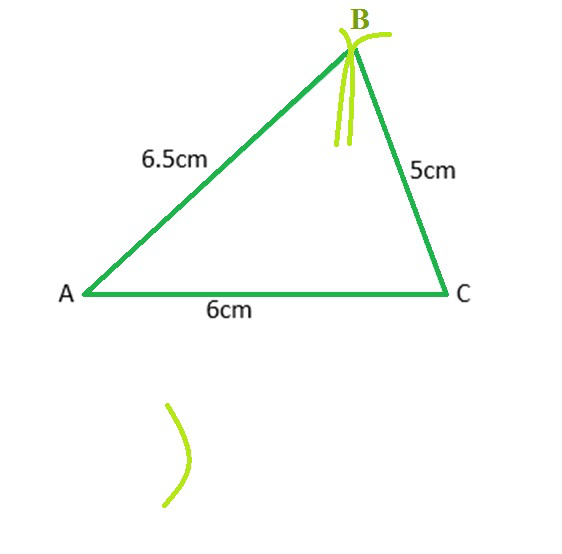
步骤 3：以 C 为中心画一个半径为 4.5 厘米的圆弧。

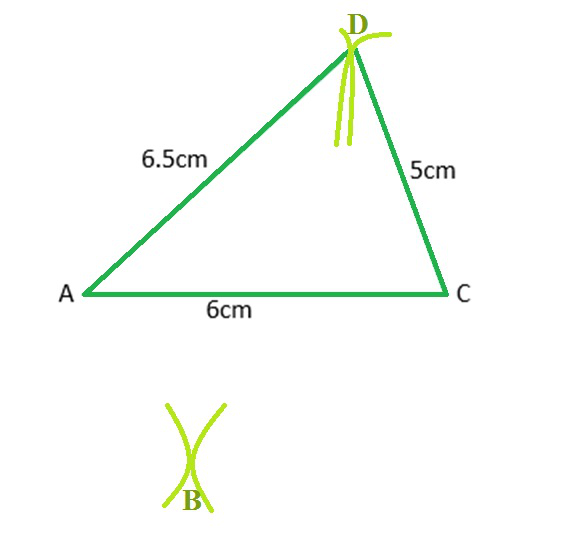
步骤4：由于B位于两条圆弧上，因此B是两条圆弧的交点。ABCD即为所需的四边形。

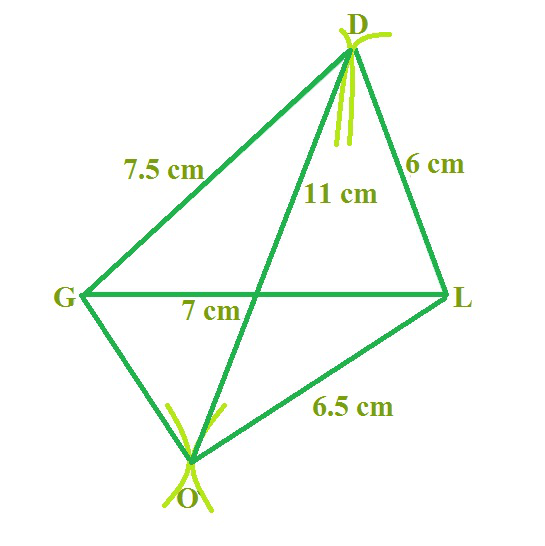
示例问题：构造一个四边形 GOLD，给定以下

OL = 6.5 厘米，GL = 7 厘米，GD = 7 厘米，LD = 6 厘米，OD = 11 厘米

回答： 

按照与上述类似的步骤，我们可以构造四边形 GOLD，其具有以下给定

OL = 6.5 厘米

GL = 7厘米

GD = 7.5厘米

LD = 6厘米

外径 = 11 厘米

因此，需要四边形 GOLD。

如果给定四边形的两条相邻边和三个角：

按照以下步骤绘制四边形：

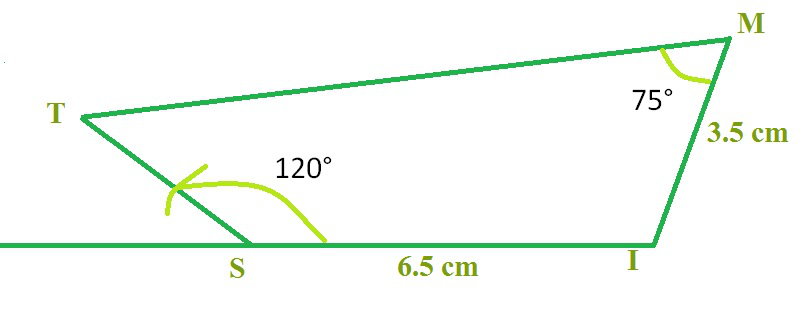
构造一个四边形 MIST，其中 MI = 3.5 厘米、IS = 6.5 厘米、∠M = 75°、∠I = 105° 和 ∠S = 120°。

先画一个草图。

步骤 1：我们首先定位点。

步骤 2：在 S 处构造 ∠IST = 120°

步骤3：在M处构造∠IMT = 75°。

步骤4：我们得到所需的四边形MIST。

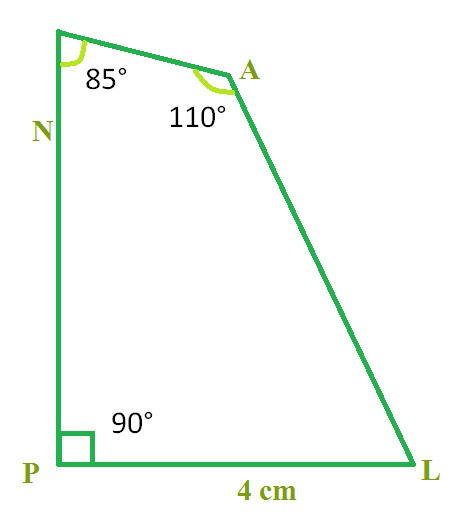
示例问题：根据给定的

PL = 4 厘米、LA = 6.5 厘米、∠P = 90°、∠A = 110° 和 ∠N = 85 °

回答：

如果给定四边形的三条边和两个夹角：

按照以下步骤绘制四边形：

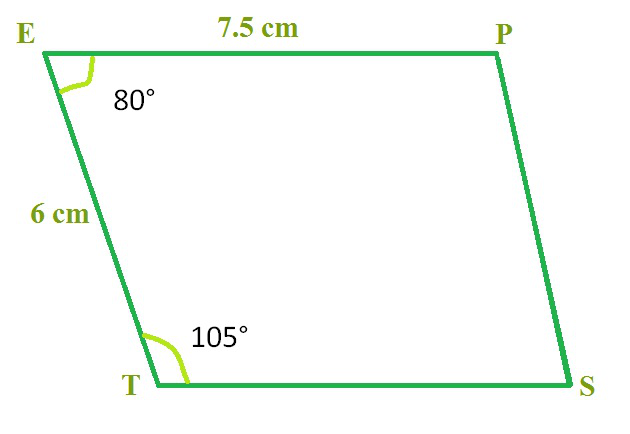
构造四边形 ABCD，其中 ST = 5 cm，TE = 6 cm，EP = 7.5 cm 且∠T = 105° 和∠E = 80°。

首先绘制草图

步骤 1：首先取 TE = 6 cm，沿 TX 画一个 105° 的角度。

找到距离此处 5 厘米的点。现在我们有 T、E 和 S

步骤2：第四点P位于EY上，EY与TE成80°角。故令∠TEY = 80°，位于TE上的C点。

步骤3： D位于EY上7.5厘米处。以E为圆心，画一条长7.5厘米的圆弧。该圆弧与EY交于P点。

步骤4：完成四边形步骤。

步骤5： STEP是所需的四边形。

如果已知四边形的其他特殊性质：

按照以下步骤绘制四边形：

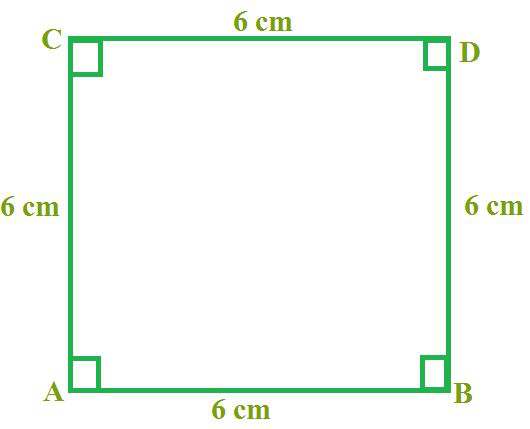
问题1：画一个边长为6cm的正方形。

回答： 

我们看到，虽然只给出了边长，但我们知道正方形是一个特殊的图形，所有角都等于直角。我们可以利用这个信息画出正方形。

步骤1：画出一个粗略的图形。

第二步：以6cm为底边画一条线AB。

步骤 3：在顶点 A 和 B 处画直角。

步骤4：沿A、B两点分别画出的射线剪开6cm。

步骤5：分别命名切点C和D。

步骤 6：加入 CD。

第七步： ABCD 就是所需的正方形。

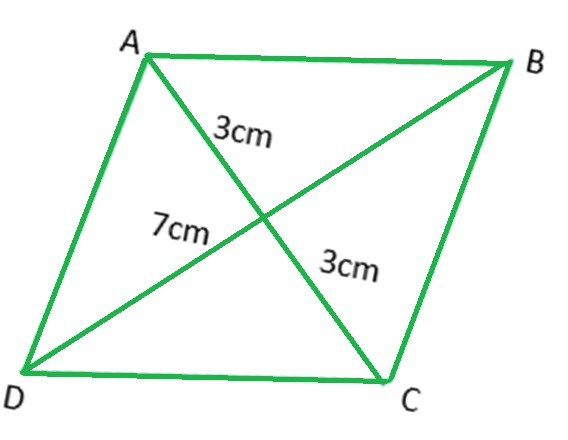
问题 2：构造一个菱形 ABCD，其中 AC = 6 厘米，BD = 7 厘米。

回答： 

给出了两条对角线的测量值。众所周知，

菱形的对角线是彼此垂直的平分线。

步骤 1：首先我们画出 AC=6cm，然后画出它的垂直平分线。

第 2 步：让它们在 0 处相遇。

步骤 3：沿所画的角平分线两侧剪掉 3 厘米的长度。

步骤 4：我们得到 B 和 D。

第五步：连接这些线，我们就得到了所需的菱形 ABCD。

参考：Construction of a Quadrilateral - GeeksforGeeks 

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。