对称的二叉树

题目描述：

请实现一个函数，用来判断一棵二叉树是不是对称的。
如果一棵二叉树和它的镜像一样，那么它是对称的

样例：

如下图所示二叉树[1,2,2,3,4,4,3,null,null,null,null,null,null,null,null]为对称二叉树：

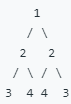
如下图所示二叉树[1,2,2,null,4,4,3,null,null,null,null,null,null]不是对称二叉树：

分析：

判断一棵二叉树是否对称，就是看该二叉树和其镜像是否相同。
求二叉树镜像的过程是：前序遍历二叉树，若当前节点的孩子节点不为空，则将二者交换，当交换完所有非叶节点的孩子节点后，就得到了树的镜像。
第一种方法是采用通过对二叉树前序遍历得到的结果和二叉树的镜像前序遍历的结果相比较，这个过程需要将二叉树转换成镜像，如果定义一种遍历方式在原二叉树上操作呢？
前序遍历是先遍历父节点，然后遍历左节点最后右节点。为了判断二叉树是否对称，我们定义对称的前序遍历，比较该二叉树前序遍历和对称前序遍历的结果是否一致。在判断的过程中若二者中值不相等或者只有一个为空则返回false。

    public boolean isSymmetric(TreeNode root) {
        if(isSymmetric(root,root))
        	return true;
        return false;
    }
	public boolean isSymmetric(TreeNode root1,TreeNode root2) {
        if(root1==null&&root2==null)
        	return true;
        if(root1==null||root2==null)
        	return false;
        if(root1.val!=root2.val)
        	return false;
        boolean left=isSymmetric(root1.left,root2.right);
        boolean right=isSymmetric(root1.right,root2.left);
        return left&&right;
    }
    //执行用时 : 2 ms, 在Symmetric Tree的Java提交中击败了89.83% 的用户
	//内存消耗 : 34.6 MB, 在Symmetric Tree的Java提交中击败了88.16% 的用户

//层次遍历
public boolean isSymmetric(TreeNode root) {
		Queue<TreeNode> q=new LinkedList<>();
		Queue<TreeNode> p=new LinkedList<>();
		q.offer(root);
		p.offer(root);
		while(q.size()>0) {
			TreeNode t1=q.poll();
			TreeNode t2=p.poll();
			if(t1==null&&t2!=null||t2==null&&t1!=null)
				return false;
            if(t1!=null&&t2!=null&&t1.val!=t2.val)
                return false;
			if(t1!=null) {
				q.offer(t1.left);
				q.offer(t1.right);
			}
			if(t2!=null) {
				p.offer(t2.right);
				p.offer(t2.left);
			}
		}
		return true;
	}
//执行用时 : 4 ms, 在Symmetric Tree的Java提交中击败了56.61% 的用户
//内存消耗 : 34.4 MB, 在Symmetric Tree的Java提交中击败了92.46% 的用户