Week - 2 - ttl

1. Rewrite the following for-loop into a while loop.

input m

x = 0

for i = 1 to m do

begin

x = x + i

end

output x

2. Rewrite the above for-loop into a repeat loop.

3. List the following functions from lowest order to highest order of magnitude:

O(1), O(n2), O(n3), O(n), O(log n), O(log2 n), O(n log n), O(√𝑛), O(n2 log4 n), O(n3/2 ), O(n10/3 ), O(n4).

从低到高排列：

1. O(1)

2. O(log n)

3. O(log² n)

4. O(√n)

5. O(n)

6. O(n log n)

7. O(n²)

8.O(n² log⁴ n)

9. O(n³/2)

10. O(n³)

11. O(n¹⁰/³)

12. O(n⁴)

O(n² log⁴ n) 的增长速度大于 O(n²) 但小于 O(n³)

4. Prove that the function f(n) = 3n2logn + 2n3 + 3n2 + 4n is O(n3). (That is, show that there exists constants c and n0 such that f (n) ≤ cn3 for all n > n0 .)

 

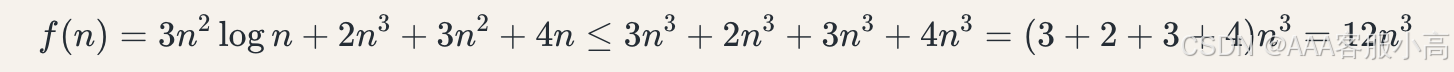
 5.

Algorithm IsCharacterUnique(T, C):

 count = 0  
  for i = 0 to n-1 do

    begin
        if T[i] == C then
        count = count + 1  

    end
  if count == 1 then
    return "Yes, the character appears uniquely."
  else
    return "No, the character does not appear uniquely."