week 3 - Data Collection & Data Distribution

如何理解世界，以及AI发展中的关键要素

• VUCA (Volatility, Uncertainty, Complexity, Ambiguity):

• Volatility（波动性）：指的是世界中快速和剧烈的变化。例如，市场或技术的快速变化会增加波动性。

• Uncertainty（不确定性）：世界充满了无法预测的情况。我们不能确定未来的事件或其后果。

• Complexity（复杂性）：指事物或系统的结构和行为具有高度的复杂性。这种复杂性可能源自多个因素的相互作用。

• Ambiguity（模糊性）：在不明确的信息下，无法做出清晰的判断或决策。

• UACC (Uncertainty, Ambiguity, Complexity, Changeability):

这与VUCA类似，但加入了Changeability（可变性），指的是世界的快速变化及其不可预测性，AI系统必须具备适应这些变化的能力。

• AI的发展方法论:

• Modeling the world（建模世界）：AI的目标之一是通过建模来理解和预测世界的行为。这包括观察、测试、记录、分析、预测等步骤。

方法学（Observation-Testing-Record-Analysis-Prediction-Response-Action）:

• 观察：收集数据和观察环境。

• 测试：验证假设或做出初步的尝试。

• 记录：整理和保存数据。

• 分析：从数据中提取有用的信息，理解其模式。

• 预测：基于分析结果，预测未来事件。

• 回应和行动：根据预测结果做出响应，并采取行动。

如何建模世界以及AI发展的关键要素

 AI发展所需的关键要素：

• 算法（Algorithm）：AI系统的核心是算法，它们为AI模型提供计算规则和逻辑框架。

• 计算能力（Computer Power）：随着AI模型的复杂性增加，计算资源变得至关重要。强大的计算能力使得更大、更复杂的模型能够高效运行。

• 大数据（Big Data）：大数据为AI提供了训练和验证的基础。没有海量数据，AI的学习和推理过程就无法进行。

机器学习的分类：

• 监督学习（Supervised Learning）：在这种方法中，AI通过学习有标签的数据来进行预测或分类。

• 无监督学习（Unsupervised Learning）：AI从没有标签的数据中找到数据的结构或模式。

• 强化学习（Reinforcement Learning）：AI通过与环境的互动，学习如何通过奖励和惩罚来最大化其行为。

深度学习（Deep Learning）：

• 深度神经网络（Deep Neural Networks）：包括多层的神经元结构，深度学习已广泛应用于图像识别、语音识别等领域。

进化计算（Evolutionary Computation）：

• 进化算法：模拟自然界的进化过程，通过遗传、变异、选择等方式，优化问题的解决方案。

如何收集数据以建模世界？

• 实验和抽样：在建模世界时，如何收集数据成为关键。使用“奶先加还是糖先加”的问题作为例子，这一实验通过统计方法进行验证。

• 这种问题利用实验设计和抽样方法来收集数据，验证假设。通过控制变量，确定奶和糖的顺序对味觉的影响。

• 统计学的革命：这张图片提到的《The Lady Tasting Tea》一书介绍了统计学如何在20世纪改变了科学，尤其是通过实验和抽样方法让我们更好地理解世界。

机器学习中的数据收集：步骤、方法和最佳实践

数据收集的流程：

• 原始数据收集：数据收集的第一步是获取原始数据，通常需要通过不同的渠道（如传感器、数据库、网络等）来获取。

• 数据清洗与预处理：原始数据往往包含噪音或缺失值，因此需要进行清理和预处理，使其适用于后续的分析和建模。

• 模型训练和测试：使用清洗后的数据来训练模型，并进行验证和测试，评估模型的准确性和泛化能力。

• 预测：训练后的模型用于做出预测，基于现有数据预测未来的趋势或结果。

• 商业计划和策略：最终，预测的结果可以帮助公司制定决策，优化商业策略。

• VUCA和UACC强调了现代世界的复杂性和不确定性，AI的建模过程帮助我们应对这些挑战。

• 数据收集是建模过程的起点，良好的实验设计和数据处理方法（如清洗和预处理）是成功的前提。

你上传的多张图片包含了关于机器学习数据收集的步骤、方法与最佳实践的内容，下面我将详细阐述并总结每张图片的知识点。

数据收集的来源、方法和数据存储

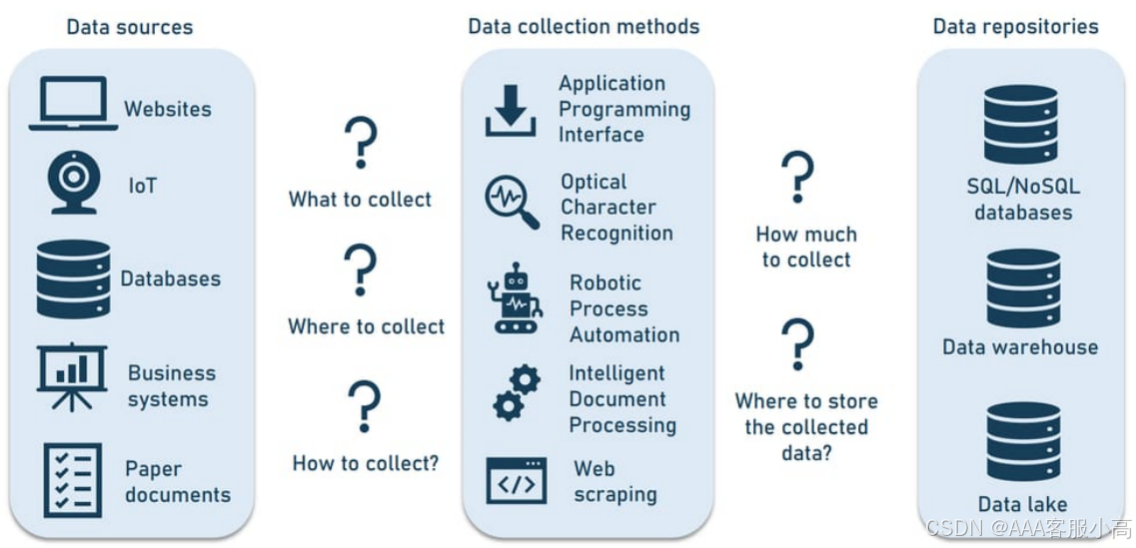
数据来源 (Data Sources):

• 网站 (Websites)：从网站上收集数据，常见的方法有爬虫（Web Scraping）。

• 物联网 (IoT)：通过智能设备获取实时传感数据，如传感器、监控设备等。

• 数据库 (Databases)：从数据库中提取结构化数据，例如通过API连接到SQL或NoSQL数据库。

• 商业系统 (Business Systems)：公司内的管理系统，如ERP系统，可能存储有业务相关的数据。

• 纸质文档 (Paper Documents)：通过OCR（光学字符识别）技术从纸质文档中提取数据。

 数据收集方法 (Data Collection Methods):

• API：通过API（应用程序接口）从不同的数据源获取数据。

• 光学字符识别 (OCR)：将扫描的文档或图片中的文字转化为可以分析的数字数据。

• 机器人流程自动化 (RPA)：通过自动化的机器人执行数据收集任务。

• 智能文档处理 (Intelligent Document Processing)：自动识别并提取文档中的信息，帮助企业数字化处理。

• Web Scraping：使用网络爬虫技术从网页上抓取数据。

数据存储位置 (Data Repositories):

• SQL/NoSQL数据库：存储结构化数据或非结构化数据。

• 数据仓库 (Data Warehouse)：集中存储来自不同来源的数据，以便进行分析和报告。

• 数据湖 (Data Lake)：存储大量结构化和非结构化的数据，通常用于数据分析、机器学习等。

数据收集：结构化数据、非结构化数据和半结构化数据

结构化数据 (Structured Data):

• 数据通常以表格形式存储，具有明确的行和列（例如，数据库中的数据表）。

• 常见存储：关系型数据库，如MySQL、SQL Server等。

• 数据模型：关系型数据模型。

• 分析方法：使用SQL查询、数据挖掘等技术进行分析。

非结构化数据 (Unstructured Data):

• 数据没有固定的格式，通常是文本、图像、音频和视频等形式。

• 常见存储：文件系统、数据湖、云数据仓库。

• 数据特点：没有固定的模式，难以直接分析。

• 分析方法：可以使用自然语言处理（NLP）、图像识别、视频分析等技术进行分析。

• 半结构化数据 (Semi-structured Data):

• 数据有某种程度的结构，例如XML、JSON等格式的数据。

• 常见存储：NoSQL数据库（如MongoDB、Cassandra）。

• 数据特点：有部分结构，但不完全符合传统数据库的模式。

• 分析方法：可以使用查询语言、数据挖掘等技术进行分析。

数据仓库、数据湖与数据集市的比较

 数据仓库 (Data Warehouses):

• 用途：主要用于组织内部的大规模数据分析和报告需求。

• 数据存储：主要存储处理后的结构化数据，支持大规模的数据分析。

• 易用性：设置相对复杂，需要较高的技术要求。

• 数据源：可以包含外部和内部的数据源，覆盖公司不同的业务领域。

数据湖 (Data Lakes):

• 用途：用于存储不同种类的数据，包括结构化和非结构化的数据，适用于大规模的数据存储和处理。

• 数据存储：包含大量原始数据，且以原始格式存储。

• 易用性：设置较复杂，通常用于处理更复杂的分析需求。

• 数据源：可以包含任何内部或外部数据源。

数据集市 (Data Marts):

• 用途：专门为特定的部门或主题提供数据支持。

• 数据存储：通常存储较小量的结构化数据，适合业务部门使用。

• 易用性：较容易搭建，适合较为专注的部门或业务场景使用。

数据收集的六种方法和2025年的数据指南

 数据收集方法 (Methods of Collection):

• 众包 (Crowdsourcing)：通过大量外部人员参与来收集数据。

• 管理数据收集 (Managed Data Collection)：数据收集由专门的团队管理和监督。

• 自动化数据收集 (Automated Data Collection)：使用技术手段自动收集数据，降低人工干预。

• 自动化数据生成 (Synthetic Data)：通过生成模型创造模拟数据，用于机器学习等。

• 授权数据集 (Licensed Data Sets)：购买或授权使用外部数据集。

• 机构合作 (Institutional Partnerships)：通过与学术机构或其他企业的合作来获取数据。

数据类型（Data Types）

在数据挖掘和机器学习中，数据通常根据其特征划分为不同类型，这对于选择合适的算法至关重要。

1. 数值型数据 (Numeric Data)：

• 连续数据 (Continuous Data)：能够在一个区间内取任意值，如温度、时间、身高等。常见的数据类型有浮动型和区间型。

• 离散数据 (Discrete Data)：只能取特定的整数值，如计数（例如学生人数、物品数量）等。

2. 分类数据 (Categorical Data)：

• 二元数据 (Binary Data)：这是分类数据的一个特殊情况，仅包含两种类别值，如0/1或真/假（例如，性别、是否购买）。

• 有序数据 (Ordinal Data)：分类数据具有明确的顺序或等级。例如，评级（从1星到5星）、教育程度（初中、高中、大学）等。

矩形数据结构 (Rectangular Data)

矩形数据是数据挖掘和机器学习中常用的数据结构。

1. 数据框架 (Data Frame)：

• 矩形数据框架类似于电子表格，包含行和列。这是数据分析中常用的基本数据结构。

2. 特征 (Feature)：

• 数据表格中的每一列通常被称为特征（例如，身高、体重、年龄等）。这些特征用于机器学习模型中的输入变量。

3. 结果 (Outcome)：

• 在许多数据科学项目中，目标是预测某种结果（通常是是/否的二元结果）。例如，预测某人是否会购买产品。

4. 记录 (Records)：

• 数据表中的每一行通常称为记录（例如，每一位顾客的详细信息，或每个实验中的每一项观测结果）。

位置估计（Estimates of Location）

在数据分析中，了解数据的集中趋势（位置估计）对于总结数据至关重要。

1. 均值 (Mean)：

均值是所有数据值的总和除以数据点的数量，通常称为平均值。

2. 加权均值 (Weighted Mean)：

 加权均值考虑每个数据点的权重，常用于对不同重要性的数据进行平均。

3. 中位数 (Median)：

中位数是排序数据中间的值，50%的数据在它之上，50%的数据在它之下。

4. 分位数 (Percentile)：

分位数指的是一个值，使得数据集中有P%的数据小于这个值，剩余的（100 - P）%的值大于这个值。

位置估计的进阶（Estimates of Location - Advanced）

1. 加权中位数 (Weighted Median)：

加权中位数考虑了每个数据点的权重，权重较大的数据点对最终的中位数位置有更大的影响。

该值使得排序后的数据中一半的权重之和位于其上方，另一半位于其下方。

2. 修剪均值 (Trimmed Mean)：

修剪均值是去除一部分极端值（extreme values）后，剩余数据的均值。常用于避免异常值对均值计算的影响。

3. 稳健性 (Robust)：

稳健性指的是数据估计对极端值的免疫能力。在数据中存在噪声或异常值时，稳健估计方法仍能提供可靠的结果。

4. 异常值 (Outlier)：extreme value

异常值是指与数据集中的大多数数据点显著不同的值。异常值可能会干扰数据分析，通常需要被标记并进行处理。

变异性度量（Variability Metrics）

变异性度量是描述数据分布和变化范围的工具。

1. 偏差 (Deviations)：

偏差是观察值与期望值或均值之间的差异。例如，预测误差和回归模型的残差（residuals）

The difference between the observed values and the estimate of location.

2. 方差 (Variance)：

 方差是各数据点与均值之间差异的平方和的平均值，度量了数据的波动性。

 The sum of squared deviations from the mean divided by n – 1 where n is the number of data values.

3. 标准差 (Standard Deviation)：

标准差是方差的平方根(square root)，是衡量数据分布的标准度量。

4. 平均绝对偏差 (Mean Absolute Deviation)：

是所有数据点与均值之间绝对偏差的平均值，常用来衡量数据分散程度。

5. 中位数绝对偏差 (Median Absolute Deviation)：

计算数据点偏差的中位数。与平均绝对偏差相比，它更不容易受到异常值的影响。

变异性度量的进阶（Variability Metrics - Advanced）

在数据分析中，变异性度量帮助我们理解数据的分布和离散情况。

1. 范围 (Range)：

范围是数据集中的最大值与最小值之间的差异，简单但有时容易受异常值的影响。

2. 秩统计量 (Order Statistics)：

是一种基于数据值从小到大排序的度量方法。它涉及通过排序数据来获得某些位置的值

 Metrics based on the data values sorted from smallest to biggest.

3. 分位数 (Percentile)：

分位数反映了数据中百分比小于某个值的数据点。例如，第50百分位就是中位数。

4. 四分位距 (Interquartile Range, IQR)：

四分位距是数据的第75百分位数与第25百分位数之间的差值，常用于描述数据的离散程度。

总结：

• 数据类型：有数值型、分类型等不同的数据类型，选择合适的算法需要根据数据的类型进行。

• 位置估计：了解数据的中心趋势对于数据分析至关重要，常见的有均值、中位数、分位数等。

• 变异性度量：通过计算数据的偏差、方差、标准差等，可以量化数据的分布和变化。

Degrees of Freedom, and n or n – 1?

• 方差公式中的分母：当我们用样本来估算总体的方差时，如果使用 n 作为分母，估算出来的方差会低于实际的总体方差，这被称为有偏估计（biased estimate）。而如果使用 n - 1，则可以得到无偏估计（unbiased estimate），即更接近实际总体的方差值。

• 自由度：自由度的概念是，估算方差时，数据点之间是互相依赖的。具体来说，样本的标准差依赖于样本均值，因此使用 n - 1 而非 n 来消除这种依赖，保证估算的方差是无偏的。

• 结论：对于大样本数据来说，使用 n 和 n-1 在实际计算中差异不大，但在理论上，使用 n-1 更能准确估计总体方差。数据科学家在解决大多数问题时，不需要特别担心自由度。

Exploring the Distribution

探索数据分布的工具和图表，包括：

• Boxplot（箱形图）：通过五个关键统计量（最小值、第一四分位数、中位数、第三四分位数和最大值）来可视化数据的分布情况。它常用于识别异常值。

• Frequency table（频率表）：记录数据值在某些区间（即“箱”）内的出现次数或频率，便于统计分析。

• Histogram（直方图）：是频率表的可视化，展示数据分布。直方图将数据划分为不同的区间（箱），并统计每个区间的数据数量或频率。需要注意的是，直方图与条形图（bar chart）不同，后者用于类别数据。

• Density plot（密度图）：密度图是直方图的平滑版本，通过核密度估计来估计数据的分布。这种图表帮助我们更清晰地看到数据的分布趋势。

Exploring Categorical Data

探索分类数据的方法：

• Mode（众数）：数据集中最常出现的类别或值，反映数据的集中趋势。

• Expected value（期望值）：当类别与数字值相关联时，通过类别出现的概率来计算的平均值。

• Bar charts（条形图）：显示每个类别的频率或比例，通常用于展示类别变量的分布情况。

• Pie charts（饼图）：类似于条形图，但以扇形的方式展示每个类别的比例，适用于少数类别的展示。 each category plotted as wedges in a pie

Correlation

相关性

• Correlation coefficient（相关系数）：衡量两个数值变量之间关联程度的指标，值的范围从 -1 到 +1。相关系数的绝对值越接近 1，表示相关性越强；越接近 0，表示相关性越弱。

• Correlation matrix（相关矩阵）：展示不同变量之间相关系数的表格，行和列是变量，表中的每个值代表变量之间的相关系数。

• Scatterplot（散点图）：通过散点图展示两个变量的关系，横轴表示一个变量的值，纵轴表示另一个变量的值。适用于观察两个变量之间的线性关系。

Exploring Two or More Variables

两个或多个变量之间关系的图表类型：

• Contingency table（列联表）：展示两个或多个分类变量之间频数的表格。它有助于理解变量之间的相互关系，尤其是对于分类数据。

• Hexagonal binning（六边形分箱）：通过将数据点分到六边形区域中来表示两个数值变量的关系。这种方法尤其适用于大量数据点的可视化。

• Contour plot（轮廓图）：展示两个数值变量之间的密度，就像是一个地形图，轮廓线表示相同的密度值。 like a topographical map（地形图）

• Violin plot（小提琴图）：类似于箱形图，但在展示数据分布时，加入了密度估计，形态类似于小提琴，因此得名。这种图表能够更细致地展示数据的分布情况。

 

 

 

 

 

Population versus sample

总体和样本之间的区别：

• Population（总体）：是数据集中包含所有可能观察对象的集合。总体的分布通常呈现理想的形态，如正态分布。

• Sample（样本）：是从总体中抽取的一部分数据，样本的分布通常是样本数据的一个近似值，可能有一些偏差或噪声。

Random Sampling（随机抽样）

相关概念：

• Sample（样本）：从一个更大的数据集或总体中提取的一个子集。

• Population（总体）：数据集的整体，通常是一个较大的数据集，或者表示总体的某个数据集合。

• N (n)：总体（样本）的大小。

• Random sampling（随机抽样）：通过随机方式从总体中抽取样本。

• Stratified sampling（分层抽样）：将总体划分为多个层次，然后从每个层次中随机抽取样本。

Dividing the population into strata and randomly sampling from each strata（层次）. Stratum (pl., strata)         A homogeneous（同种类的）subgroup of a population with common characteristics.

• Bias（偏差）：指系统性误差。

• Sample bias（样本偏差）：样本没有代表总体，或者样本有偏。

随机抽样的目的是为了确保样本尽可能准确地代表总体，从而得出有效的结论。

---

 Selection Bias（选择偏差）

相关概念：

• Selection bias（选择偏差）：指由于选择观察对象的方式不当，导致样本不能代表整个总体。

• Data snooping（数据窥探）：指在数据中大量搜索有趣的模式或信息，可能会导致无效的统计结论。（过拟合Overfitting）

• Vast search effect（庞大搜索效应）：由于反复建模或使用大量预测变量建模数据，可能导致偏差或不可重复性。

---

Sampling Distribution（抽样分布）

相关概念：

• Sample statistic（样本统计量）：从样本数据中计算出的指标，用于估计总体参数。

• Data distribution（数据分布）：数据集中每个值的频率分布。

• Sampling distribution（抽样分布）：从多个样本或重采样（resamples）中得到的样本统计量的频率分布。

• Central limit theorem（中心极限定理）：随着样本量的增加，抽样分布趋向正态分布。

• Standard error（标准误差）：样本统计量的变异度（标准差standard deviation），用于度量样本统计量的稳定性。

样本统计量的变异性（variability）指的是样本统计量在多次抽样中的变化程度。当我们从总体中抽取多个样本时，计算得到的每个样本统计量（比如样本均值、样本方差等）可能会有所不同。标准误差（Standard Error, SE）就是衡量这些样本统计量（如样本均值）变化的程度

标准误差：

• 标准误差与标准差不同，它衡量的是样本统计量（如样本均值）在多次抽样中的变异性。因此，它反映了通过一个样本来估计总体参数时的准确性或不确定性。

• 标准误差随着样本量的增加而减小，因为更大的样本通常会更接近总体的真实特征。

---

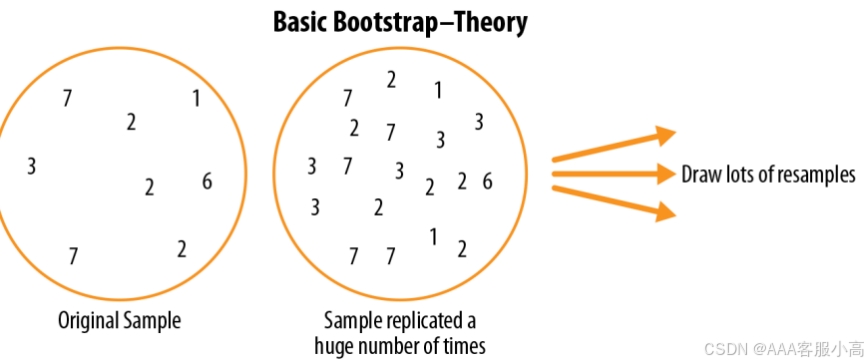
Bootstrap（自助法）

• Bootstrap sample（自助样本）：从已观察的数据集中有放回地抽取样本。

• Resampling（重采样）：从已观察的数据中进行重复抽样，包括自助法和置换（洗牌）程序。

从观测数据中重复取样的过程，包括了两种主要的方法：自助法（bootstrap）和置换法（permutation，也称作洗牌法shuffling）。自助法是一种通过从原始数据集中重复抽取样本来构建新的数据集的方法，它允许我们估计统计量的分布，尤其是当原始数据集较小或分布未知时。置换法则是通过在不改变数据本身的情况下，随机改变数据的排列顺序来模拟随机性，从而评估统计推断的稳健性。

自助法是一种重采样技术，主要通过从原始数据集中有放回地抽取样本来构建新的样本。这个过程可以重复进行，从而估算出样本统计量的分布。它广泛应用于不依赖于正态分布假设的统计分析中。

---

 Multivariate Bootstrap Sampling（多变量自助法抽样）

多变量自助法是指在多维数据上进行重采样，通过从多维样本空间中反复抽样来估计参数分布。这种方法尤其适用于多变量数据分析，能够揭示数据中变量间的关系。

---

Confidence Intervals（置信区间）

用于评估和表达基于样本数据的估计值的可靠性

• Confidence level（置信水平）：置信水平表示的是在无限多次重复实验中，所构建的置信区间包含真实总体参数的比例。简单来说，置信水平告诉我们有多大把握相信某个区间包含真实的总体参数。

置信区间是基于样本数据构建的一个区间估计，用于表示我们对总体参数（如总体均值或总体比例）的估计范围。置信区间不仅给出一个点估计，还给出了一个区间，说明总体参数在该区间内的概率。

• 置信区间 是一个范围，表示我们估计总体参数可能落入的区间。

• 置信水平 则是表示这个区间的准确性和可靠性的概率，描述了在多次抽样中，构建的置信区间包含真实总体参数的可能性。

• Interval endpoints（区间端点）：置信区间的上下限。

置信区间为我们提供了一个范围，这个范围有一定的概率包含总体参数。置信区间的置信水平通常为95%或99%，表示在多次实验中，95%或99%的置信区间将包含真正的总体参数。

正态分布（Normal Distribution）

• 误差（Error）：误差是数据点与预测值或均值之间的差异。也就是实际观测值与模型预测值或理想平均值之间的偏差。

• 标准化（Standardize）：标准化是通过将数据值减去均值并除以标准差来将数据转换为标准正态分布。标准化的目的是消除原始数据单位的影响，便于比较不同数据集。

• z-score（Z分数）：Z分数是标准化后的数据点，它表示数据点距离均值的标准差个数。计算公式是：

• 标准正态分布（Standard normal）：标准正态分布是均值为 0，标准差为 1 的正态分布。标准正态分布常常用来计算Z分数，帮助我们理解数据点与均值之间的关系。

• QQ-图（Quantile-Quantile Plot）：QQ图是一种可视化工具，用于比较样本分布和理论分布（如正态分布）之间的匹配程度。通过在图中绘制样本分位数与理论分位数的关系，QQ图帮助我们判断数据是否遵循正态分布。

正态曲线（Normal Curve）

这张图展示了正态分布的特性，强调了标准正态分布（均值为0，标准差为1）中的数据分布。

• 68-95-99.7规则：该规则描述了正态分布数据的集中趋势：

• 68% 的数据位于均值的 ±1 标准差 范围内。

• 95% 的数据位于均值的 ±2 标准差 范围内。

• 99.7% 的数据位于均值的 ±3 标准差 范围内。

这意味着在标准正态分布中，大部分数据会集中在均值附近，随着数据距离均值越来越远，出现的概率迅速降低。

长尾分布（Long-Tailed Distributions）

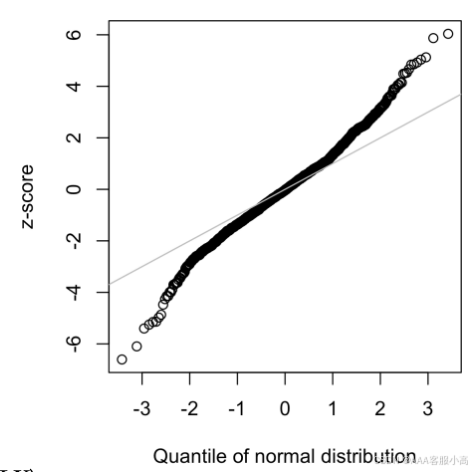
• 尾部（Tail）：长尾分布的尾部是频率分布的长而窄的部分，其中极端值出现的频率较低。尾部反映了数据集中少数非常大或非常小的值，这些值会影响分布的形态。

relatively extreme values occur at low frequency.

• 偏斜（Skew）：当分布的一侧（尾部）比另一侧更长时，分布就被称为“偏斜”。偏斜可以是：

 正偏斜（右偏）：右尾更长，意味着数据集中大部分值较小，少数较大的极端值拉长了右侧。

 负偏斜（左偏）：左尾更长，意味着大多数数据集中在较大的值，而少数较小的极端值拉长了左侧。

• QQ图：在这张图中，我们通过QQ图来检查数据是否符合正态分布。如果点大致沿着直线分布，则说明数据接近正态分布。如果出现明显的偏离直线的情况，则说明数据具有长尾或偏斜。

学生t分布（Student’s t-Distribution）

• 样本量（n）：样本量是从总体中抽取的样本的大小。t分布的形态与样本量密切相关，样本量较小的时候，t分布的尾部较长，随着样本量的增加，t分布逐渐接近标准正态分布。

• 自由度（Degrees of Freedom）：自由度是t分布的一个关键参数，它与样本量和统计量有关。自由度决定了t分布的形状。通常自由度为 n-1，其中 n 为样本量。

 A parameter that allows the t-distribution to adjust to different sample sizes, statistics, and numbers of group

t分布的尾部指的是分布曲线两侧较远的区域，这些区域代表着样本数据中极端值或异常值出现的概率。由于t分布主要用于样本量较小的情况，因此它的尾部比正态分布更宽，表示小样本数据中出现极端值的可能性较大。随着样本量的增加，t分布的尾部逐渐收窄，接近于标准正态分布。

 二项分布（Binomial Distribution）

• 试验（Trial）：是一个具有离散结果（discrete）的事件，比如投掷硬币得到正面或反面。

• 成功（Success）：试验的目标结果，例如在投掷硬币时，成功可能是得到“正面”。

• 二项分布（Binomial Distribution）：描述在一系列二项试验中成功次数的分布。每次试验都有两个可能结果（例如“成功”和“失败”），并且每次试验是独立的。二项分布的公式为：

泊松分布与相关分布（Poisson and Related Distributions）

• λ（Lambda）：是泊松分布的参数，表示单位时间或单位空间内事件的发生频率。

• 泊松分布（Poisson Distribution）：描述在一定时间或空间内，某一事件发生的次数。泊松分布通常用于事件发生次数较少的情况，例如，每小时内顾客到达商店的次数。

• 指数分布（Exponential Distribution）：描述事件发生间隔的概率分布。指数分布是泊松分布的时间反向分布，常用于描述等待时间或间隔时间。

• 威布尔分布（Weibull Distribution）：威布尔分布是一种广义的指数分布，允许事件发生的速率随时间变化。

---

总结：

1. 正态分布和标准正态分布是统计学中常见的分布类型，涉及如何标准化数据、计算Z分数以及利用QQ图可视化分布。

2. 长尾分布和偏斜分布描述了数据分布不对称的情况。

3. 学生t分布用于样本量小且总体标准差未知时的统计推断。

4. 二项分布和泊松分布分别描述离散事件（如成功与失败）和事件发生频率的分布。