五、规划控制——基于MPC的车辆控制和轨迹规划（2）

概要：本文主要学习基于MPC车辆运动模型以及目标函数的构建

---

前言

---

本文将对MPC运动学模型及目标函数进行研究。

一、车辆运动控制架构

1. 运动规划模块会生成基于运动轨迹的参考路径；
2. 运动规划模块会给出速度的参考和约束的构建（包含上层对于安全性能的考量即在哪个范围内驾驶是安全的）；
3. 将1和2作为输入给到MPC进行优化 ，它会根据反馈的测量值和模型进行预测；
4. 可以预测到时域下车辆的轨迹（predicted trajectory）和最优控制序列（Optimal control horzion）；
5. 把第一个控制量发给车的底层控制器（Low level control）最终产生油门刹车和方向盘扭矩来控制车的运动。
   （1）如果行驶足够快，则不需要使用底层控制器也可以发出油门刹车和方向盘的指令。
   （2）MPC问题构架复杂，运算量较大，长时间下很难保证系统的实时性，这种情况下需要加入底层控制器避免延时的问题，常用底层控制器：PID，可以运行在高频架构下面，保证抗干扰性能。

总结：
MPC的作用是在有限的时域内，对车辆的轨迹进行不断的迭代和优化，并且产生相对应轨迹追踪控制信号，也就是说每当收到一个新的反馈，就需要基于MOC进行新的优化，保证优化的实时性；而好的模型会让MPC生成高质量的预测状态从而保证准确性和有效性，与此同时构建的约束会对提高优化解的安全性；同时目标函数可以更好选取需要优化的量，从而最大限度保证车辆达到预期行驶的方向和轨迹追踪。

二、车辆运动控制输出

1. MPC输出基于最优轨迹追踪下有限时域的最优控制，而控制信号的选取可以根据不同的应用场景分为：
   （1）Speed / Steering angle
   （2）acceleration / steering rate
   （3）jerk（加速度变化率）/ steering acceleration

三、MPC解析

总的来说，运用MPC来控制车辆需要注意以下几个方面：

1. 模型选择，构建系统，预测未来信息（针对不同场景选择不同的颗粒度）
2. 目标函数选择（轨迹追踪、车辆控制效率和舒适度）
3. 约束的选择，保证安全性和模型准确性（满足模型、驱动力限制，基于底层控制器加入引擎关系、动力模型、执行器模型、轮胎力模型等）

3.1 车辆模型构建（Curvilinear Coordinates vehicle model）

回顾：
（1）自行车模型（运动学模型）

（2）自行车模型（动力学）

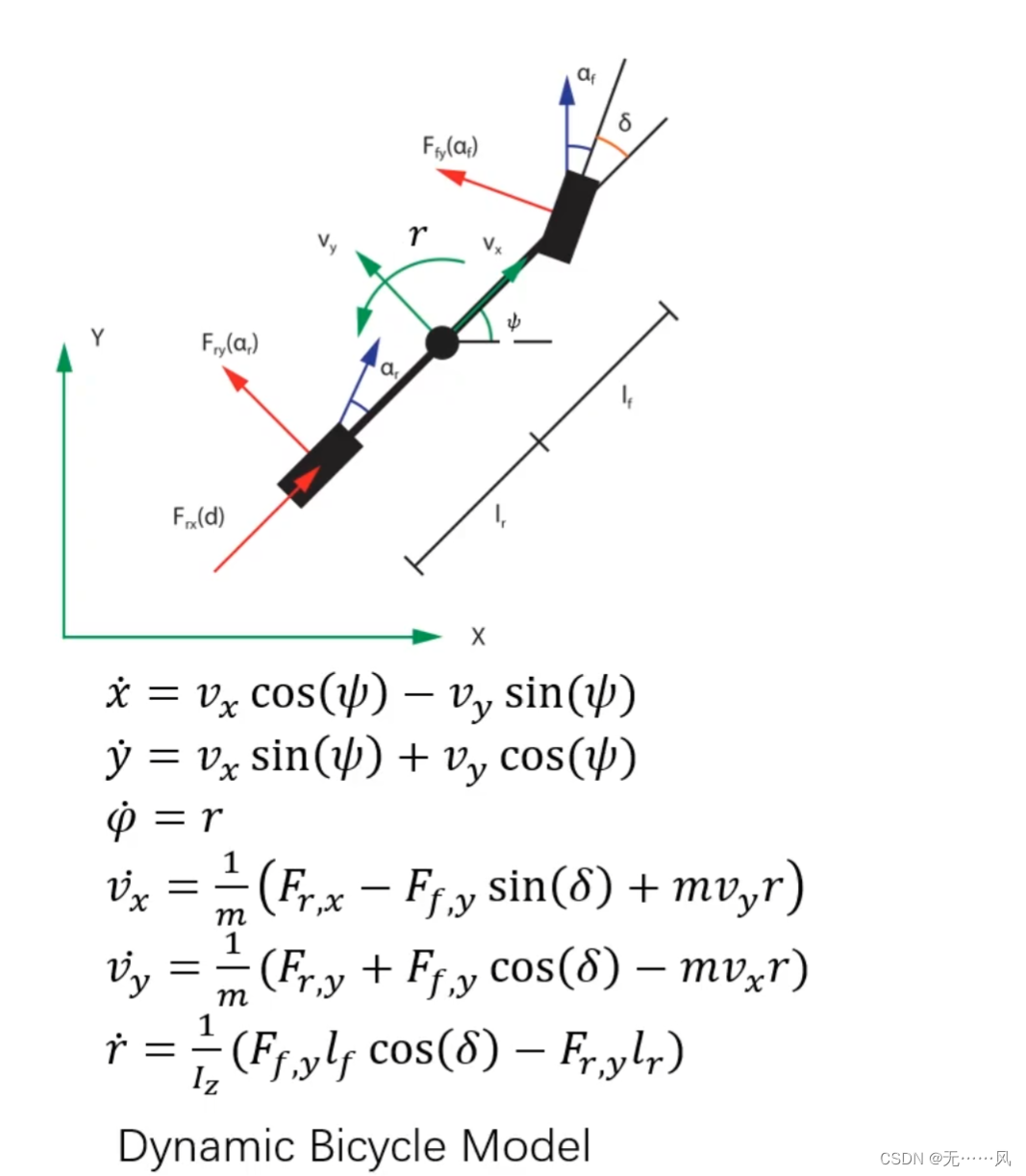
Curvilinear Coordinates vehicle model
该模型性描述车辆和参考轨迹之间关系的模型，包括车辆对于轨迹的速度和车本身速度之间关系，以及与轨迹之间侧向横向的误差、轨迹曲率建立关系。

状态量：

其中，S是路径点的行驶距离，N是车辆与路径的横向误差，u是车辆和路径横摆角的误差。V是车辆vx和vy的合速度，a是行进方向的速度变化，δ是转向角等。
有些变量是为了构建约束而设计的并不都是给到底层控制器。

输入量：

其中，Ujerk为速度的二阶微分，另一项是对转角的二阶微分。
由于积分比微分准确，所以通过二阶微分在积分可以求得速度、加速度、角速度、转角；而且输入项和舒适度是息息相关的。

3.2 车辆模型推导

可以用ds/dt来描述车辆沿着参考轨迹运动。

其中：

1. Vs为vx和vy方向上的分量，也就是参考点旋转半径R减去相对于车辆的距离n，乘以旋转角速度。
   
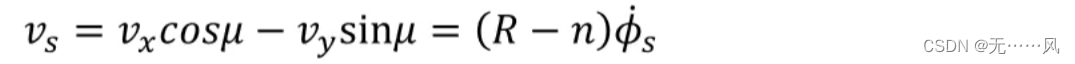
2. 参考点的旋转速度s’为R乘以旋转角速度。
   
   这样就可以建立起轨迹和车辆速度之间的关系。
3. 以路径的曲率表示旋转大小，表达式为：
   
4. 结合上述表达式，可以表示为：
   
   再通过自行车模型建立起车辆整体运动和参考轨迹之间的关系。
   
   其中，
   这时，β+μ表示为车辆速度和参考点速度之间的夹角。

横向误差的速度为：

旋转部分就是车旋转的速度R和参考点旋转速度的差值，其中Rv为lr/sinβ。

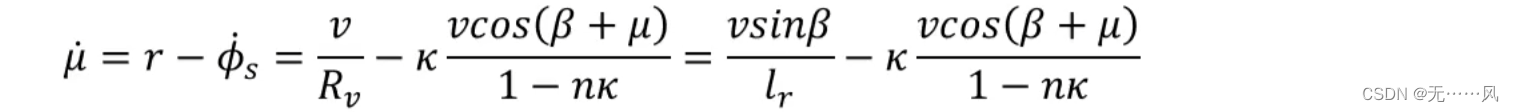
曲线坐标车辆动力学模型（非线性模型）：

该模型将纵向运动和横向运动耦合起来，以及车辆运动和运动轨迹的相对运动也建立关系。

3.3 β值解析

基于自行车模型进行求解β。

四、MPC模型选择

需要根据具体的需求和情况进行具体分析。

1. Accuracy：
   
   非线性、动力学模型、横纵向耦合。
2. Fast：
   
   线性（QP）、运动学模型（低速）、解耦合（降低模型复杂度）。

综上来看，模型并不是越准确或者越快越好，要综合分析有效选择模型。

五、车辆目标函数的构建

目标函数是优化控制核心的概念之一，它直接反应了优化的目的和期待车辆的行为，可以达到什么样的效果。

5.1 目标函数的定义

目标函数的定义有以下几个方面：

1. 参考轨迹跟踪精确度的优化，假设运动规划就已经考虑了舒适度、安全性的优化，期待车辆严格追踪参考的轨迹，就可以提高追踪轨迹的损失cost。
2. 如果在规划中并没有对路径进行平滑处理，但比较注重舒适度，那么就可以对舒适度进行目标函数的建立和调节。
3. 同时对安全性有一定的保障，所以，可以建立安全性的目标函数来保证安全性能。

一般来说，根据不同的规划控制架构，其目标函数的权重是不同的。所以，可以用不同的权重比叠加，这样可以针对不同的情况对这三个权重进行调节，

其中，wt就是对跟踪的权重，wc就是对舒适度的权重，ws就是对安全性能的权重。
当然，在不同场景下，三个权重的调节会有一个优先级的概念，如在紧急场景下，安全性就破坏了舒适度的权重。

5.2目标函数解析

5.3.1 目标函数（Tracking Objective）

跟踪规划轨迹和速度曲线。

其中，
（1）第一项为参考轨迹纵向速度的偏差的矫正；
（2）第二项为侧向偏移误差的矫正；
（3）第三项为方向误差的矫正。

5.3.2 目标函数（Comfort Objective）

其中：
（1）第一项为对于纵向加速度倒数的控制；
（2）第二项为对于纵向加速度变化的控制；
（3）第三项为对于侧向加速度变化的控制；
（4）第四项/第五项对于转向角变化/振荡的优化；
通常我们需要有选择的有侧重的选择量进行优化。

5.3.3 目标函数（Safety Objective）

通过对可行使区域的违反程度来衡量系统的安全度。

实际上，我们对系统的约束分为**软约束（可以违反）和硬约束（不能违反）**两种。

一般来说，输入约束都是硬约束，因为它有物理限制，如车辆油门移动量、电机最大转速量。
一般来说，输出约束都是软约束，因为他可能在某个场景比如爬坡工况下，即使最大化油门，速度还是起不来，违反了速度约束。所以，设置软约束避免输出和输入之间的冲突。

引入硬约束，会导致控制实现控制的复杂度增加：
（1）即使是稳定系统，可行域会受到限制；
（2）在测量和预估状态都会存在噪声或者干扰的存在，它也会使控制器超出可行的范围。
所以，在实际应用中，状态约束通常为软约束。
所以，像状态或者输入变量一样，我们引入了松弛变量，对优化器提供了边界违反的许可。
这样就将安全性的约束转变为对约束违反的惩罚。

我们可以引入松弛因子来优化违反边界的程度，从而优化安全性能。

其中，
（1）λsoft为松弛因子，包含了侧向、速度、加速度的松弛因子
（2）E代表了对这三个软约束的权重比

（3）λhard为硬约束，包含了侧向、加速度、位置的硬约束（目标车相对距离）

（4）H杠为硬约束的权重比

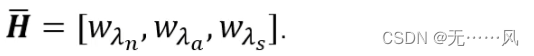
5.3.4 总结

以上就是针对不同的应用场景构建出来不同的约束包括对于参考轨迹的跟踪能力、舒适度和安全性（对于约束的违反程度）。

MPC是短视策略，每一步预测的轨迹实际上只能跟踪第一步，而且MPC是对有限时域优化的问题。所以，就会发生以下两种情况：
（1）很难保证其可行性，MPC可能没有解，常发生在很难达到的约束情况下；
（2）很难保证其稳定性，系统从初始到稳定状态需要一定时间，预测时域太短很难完成其收敛过程。
为了解决上述问题，我们需要对终端状态进行约束和优化，迫使系统的状态在预测期结束以后，在特定的集合内取值，来保证迭代的稳定性和可行性。

5.3.5 目标函数（Terminal Objective）

终端目标函数其实是施加在预测时域之后最终阶段的Cost，主要用于设计终端的代价函数来提高闭环的稳定性和总体的Cost，弥补我们没有无限优化范围的不足。

终端约束和目标函数的构建：
（1）终端约束为系统全局稳定性提供了约束条件；
（2）在实践中，增大时域，检查采样稳定性；
（3）对于小时域时长N，终端约束可以选择为0，作为最简单的选择，但是我们的吸引力区域（表征系统稳定性的特征）比较小；
（3）对于大时域时长N，我们的吸引力区域接近最大的控制不变集；
（4）没有终端约束的吸引域有时候可能比有终端约束的吸引域要大，但是对于表征吸引域比较困难。

在车辆控制应用中，可以把终端成本选择在预测时域的最后阶段，与参考路径的运动方向进行对齐，这种Cost可以保证车辆密切追踪参考轨迹，即使在控制范围之外，也可保证轨迹的连续性和平滑性。如弯道停车，预测时长可能到了停车线上，后面的路径则是在预测时域之外，所以，在其工况下，可以加入一个终端目标函数，使得最终停车的方向和后续路径的方向对齐。这样，就会帮助我们提高控制的性能。

---

总结

本文主要是对于自动驾驶规划控制中模型预测的优化控制进行学习，主要介绍了MPC运动学模型以及目标函数的构建等知识，这篇文章希望可以对想要学习自动驾驶规划控制方向的同学们有一定的帮助。
喜欢的朋友们动动小手点个关注，我会定期分享我的一些知识总结和心得体会，感谢大家!