10.矩阵覆盖

看了个寂寞

于 2020-06-12 09:00:27 发布

阅读量206

点赞数

CC 4.0 BY-SA版权

分类专栏：算法文章标签： java 递归法

本文链接：https://blog.youkuaiyun.com/gtjsjj/article/details/106708209

算法专栏收录该内容

50 篇文章

订阅专栏

本文介绍了如何使用斐波那契数列解决一个编程问题：用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形。当n分别为0、1、2时，存在特定的覆盖方法数。对于n大于2的情况，通过递归考虑两种摆放方式（一种放置2*1矩形，另一种放置1*2矩形）来计算总数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

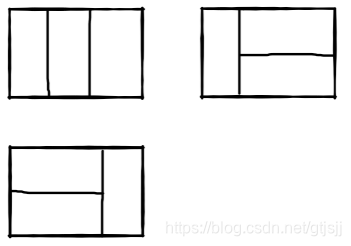
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？比如n=3时，2*3的矩形块有3种覆盖方法：

思路

链接：https://www.nowcoder.com/questionTerminal/72a5a919508a4251859fb2cfb987a0e6?f=discussion
来源：牛客网

依旧是斐波那契数列

2*n的大矩形，和n个2*1的小矩形

其中target*2为大矩阵的大小

有以下几种情形：

1⃣️target <= 0 大矩形为<= 2*0,直接return 1；

2⃣️target = 1大矩形为2*1，只有一种摆放方法，return1；

3⃣️target = 2 大矩形为2*2，有两种摆放方法，return2；

4⃣️target = n 分为两步考虑：

第一次摆放一块 2*1 的小矩阵，则摆放方法总共为f(target - 1)

第一次摆放一块1*2的小矩阵，则摆放方法总共为f(target-2)

因为，摆放了一块1*2的小矩阵（用√√表示），对应下方的1*2（用××表示）摆放方法就确定了，所以为f(targte-2)

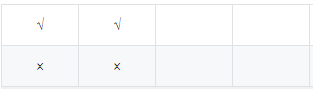
代码

public class Solution {
    public int RectCover(int target) {
        if(target==0)
            return 0;
        else if(target==1)
            return 1;
        else if(target==2)
            return 2;
        else
            return RectCover(target-1)+RectCover(target-2);
    }
}