深度优先搜索

最新推荐文章于 2025-11-29 17:03:10 发布

原创最新推荐文章于 2025-11-29 17:03:10 发布 · 93 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#剪枝 #dfs

本文探讨了八皇后问题的解决方案，利用深度优先搜索（DFS）策略，通过左右对角线限制避免冲突。同时介绍了如何在给定数列中选择特定数量的元素以达到预设和的组合优化问题，同样采用DFS进行求解。这两个问题展示了DFS在解决约束条件下搜索问题的广泛应用。

八皇后问题

八皇后问题
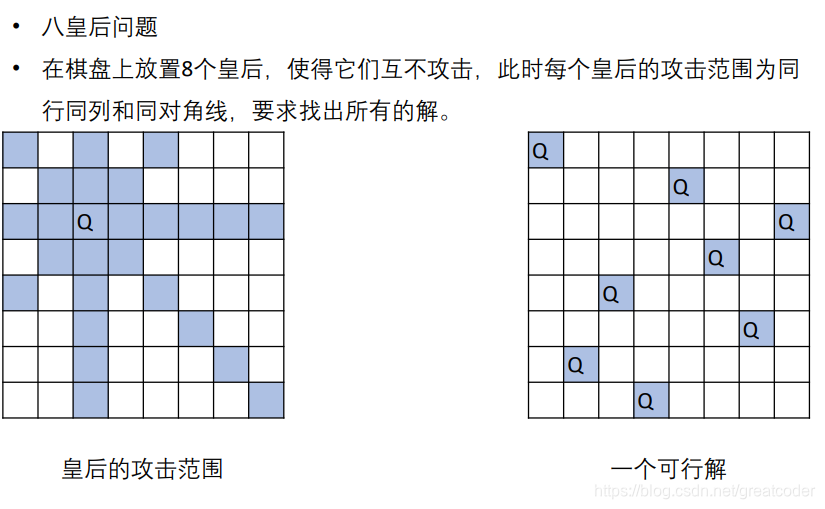
使用dfs Right数组记录了那一条从左下到右上的对角线上不能放棋子，
Right【i+ x】
例如：
i + x = 2, (i,x) = (0,2) , (1,1),(2,0) 这一条线上都不能放棋子
i + x = 5 （i，x） = （0，5），（1，4），（2，3），（3，2），（4，1），（5，0）之一条线上不能放棋子

Left【i- x + n】记录了那一条从左上到右下的对角线上不能放棋子。
推导：
同一对角线（0，0）（1，1）（2，2）
（1，2）（2，3）（3，4）
有公式y = x + b
有公式 y- x = b，因为b可能为负，y-b + n最为公式
Left[i - x + n]

const int MAXN = 1010;
bool Left[2*MAXN];
bool Right[2*MAXN];
int vis[MAXN];
int a[MAXN];//a中记录了每一列选择的行数
int ans;
void permutation(int x,int n)
{
    if(x==n)
    {
        ans++;
        for(int i = 0;i < n ;i++)
        printf("%d ",a[i]);
        printf("\n");
        return;
    }
    for(int i = 0;i < n;i++)
    {
        if(!vis[i] && !Left[i - x + n] && ! Right[i + x]){
            vis[i] = 1;
            Left[i - x +n] = 1;
            Right[i + x] = 1;
            a[x] =i;
            permutation(x+1,n);
            vis[i] = 0;
            Left[i - x +n] = 0;
            Right[i + x] = 0;
        }
    }
}

选数问题

选数问题
给定n个正整数，要求选K个数，使得选出来K个数之和为sum，求和法的方案数
K < n < 16
问题描述

int s;
int k;
int cnt++;
int a[20];
void dfs(int sum,int x,int kk)
{
    if(sum == s && kk = k)
    {
        cnt++;
        return;
    }
    if(x > n || sum > s || kk > k) return;
    //选这个数
    dfs(sum + a[x],x + 1, kk+1);
    //不选这个数
    dfs(sum, x+1, kk );

}

再卖菜CSP201909-4

再卖菜
使用dfs搜索