取模运算与快速幂

最新推荐文章于 2024-02-12 14:10:30 发布

原创最新推荐文章于 2024-02-12 14:10:30 发布 · 206 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

博客探讨了取模运算的性质，如(𝑎±𝑏) % 𝑝 = 𝑎 % 𝑝 ± 𝑏 % 𝑝 % 𝑝 和 (𝑎 × 𝑏) % 𝑝 = (𝑎 % 𝑝) × (𝑏 % 𝑝) % 𝑝。针对大数乘法，提出使用快速幂算法优化计算，将复杂度降低到𝑂(log𝑏)。示例展示了如何计算(1015 * 1016) % (109 + 7)。这种方法在处理大型数据时避免了溢出问题并提高了效率。

取模运算的一些性质

（ 𝑎 ± 𝑏 ）%𝑝 = 𝑎%𝑝 ± 𝑏%𝑝 %𝑝
(𝑎 × 𝑏) %𝑝 = （（𝑘1𝑝 + 𝑎0 ）× (𝑘2𝑝 + 𝑏0 )%𝑝) = 𝑎0 × 𝑏0 %p
即 • （𝑎 × 𝑏） %𝑝 = （𝑎%𝑝 ）× （𝑏%𝑝） % p
(10¹⁵ * 10¹⁶)%(10⁹ + 7) ,直接运算会爆long long，要用取模运算的运算规则

快速幂

计算 𝑎^𝑏 mod 𝑝 的结果 0 < 𝑎, 𝑏, 𝑝 ≤ 10⁹
• 如果直接循环计算，则需要 𝑂(𝑏) 的复杂度，会TLE
引入分治的思想

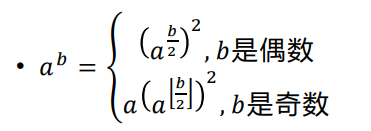
每次可以将b除2，复杂度O（logb）
和矩阵的快速幂思路完全相同。

long long qpow(long long a,long long b,long long p)
{ 
 long long ans = 0;
 for(a %=p;b;a = a*a %p,b >>=1)
 if(b & 1)
 ans = ans *a % p;
 return ans;
 
}