基于CoRAD的哑节点连接恢复

自组织传感器网络中哑节点的连接恢复

普什彭杜·卡尔、阿里吉特·罗伊和苏迪普·米斯拉，印度理工学院克勒格布尔分校

在本研究中，我们提出了一种名为CoRAD的方案，用于在静态无线传感器网络（WSN）中，当部分节点出现 “哑的”行为时，利用具有可调通信范围的传感器节点重新建立丢失的连通性。由于此类行为的发生，节点之间 可能会出现临时性连通性丢失。这一现象不同于静态无线传感器网络中常见的节点孤立问题。仅激活中间休眠节 点并不能保证连通性的恢复，因为孤立节点可能不存在邻居节点。相反，单个传感器节点通信范围的增加可能导 致其迅速死亡。此外，传感器节点的通信范围增大存在最大限制，该限制可能不足以恢复连通性。因此，综合考 虑网络自组织和孤立节点重新连接中的上述因素，我们提出了一种基于价格的方案，通过激活中间休眠节点或调 整网络中其他部分节点的通信范围来解决该问题。当哑节点在有利环境条件恢复后回归正常行为时，该方案还会 停用额外激活的节点，并降低已增加的通信范围。为实现所提方案，CoRAD需要构建由支持GPS的可调通信范 围传感器节点组成的网络。通过仿真，我们在相同场景下将所提方案与现有的拓扑管理方案LETC和A1进行比较， 比较指标包括激活节点数量、消息开销和能量消耗。结果表明，所提方案相较于现有拓扑管理方案表现出更优的 性能。

类别和主题描述符：C.2.2[Wireless Sensor Networks]：环境影响，可靠数据采集
通用术语：连通性，性能，可靠性 附加关键词和短语：哑节点，环境影响，连通性，动态收缩 e, 可调sensor节点

美国计算机协会参考格式：
普什彭杜·卡尔、阿里吉特·罗伊和苏迪普·米斯拉。2016年。含哑节点的自组织传感器网络中的连接恢复。《美国计算机协会 自主与自适应系统汇刊》第10卷第4期，文章28（2016年1月），30页。DOI:http://dx.doi.org/10.1145/2816820

1.引言

低成本且高效的集成电子设备的最新进展对无线传感器网络（WSNs）的实现产生了重大 影响，目前这些网络已广泛应用于安全、监控、灾难管理、军事、医疗保健、农业和环境 监测等领域。

[阿基尔迪兹等人，2002b；孙等人 2010]。由于传感器节点通信范围有限，无线传感 器网络采用从源节点到基站的多跳路径，在此通信过程中，一个或多个节点作为中间节点 进行协作。连通性是无线多跳网络的主要考虑因素之一[阿基尔迪兹等人，2002a]。连通网 络中，网络内每对节点之间至少存在一条路径。传感器节点之间的协作与合作是建立节点 间连通性和保障网络正常运行的重要因素[吴等人 2012]。异常行为、攻击和故障是促进传 感器节点间协作与合作需要克服的主要挑战。一个有故障的传感器节点可能在网络中造成 拥塞，无法覆盖其感知区域，丢弃接收到的数据包，或错误转发数据包[巴吉奇等人， 2014；赫伯特等人 2007]。传感器节点异常行为可能造成的影响包括丢包、路由信息或数 据包的篡改、网络拓扑的错误表示以及误导节点[德罗扎等人，2007；米斯拉等人 2009, 2010]。外部攻击者可以降低网络资源可用性，并破坏网络的完整性与机密性[卡拉 皮斯托利等人 2013]。所有这些影响都是导致网络性能下降的因素[阿布杜瓦利耶夫等人 2013]。

在本研究中，我们考虑了一种特定类型的异常行为，称为哑的行为[Misra等人 2014]。 当传感器节点由于通信范围缩小（通常是由于不利环境影响开始出现）而无法通信，并在 之后一段时间内随着有利环境条件恢复而重新恢复通信时，该节点表现为哑节点。这些哑 节点继续进行感知，但无法将感知数据传输给其他节点。因此，传感器节点的哑行为导致 可变网络连通性，产生通信空洞，造成信息丢失，并使网络部分孤立。为了应对网络中哑 节点带来的不利影响并改善网络性能，采用支持GPS的可调通信范围传感器节点重构网络 拓扑[陈等人，2007；Mir和Ko 2008],，这些节点可根据需要调整其通信范围，但会带 来额外能耗。我们还考虑了远距离路径损耗传播[Seybold 2005]以建模信道特性。当传 感器节点开始表现为哑节点并变得孤立时，哑节点会最优地增加通信范围，并激活中间的 休眠节点，以重新建立与网络的连接。通过这种方式，缓解了哑节点对网络造成的不利影 响。本文提出了一种在存在哑节点情况下利用可调传感器节点进行连通性重新建立（ CoRAD）的方案来解决这一问题。

1.1.动机

节点之间的连通性是实现多跳无线传感器网络的一个重要问题。由于雾、降雨和高温等恶 劣环境条件导致通信范围缩小，使得传感器节点表现为哑的。由于这种行为的发生，传感 器节点会从网络中孤立出来，在暂时无法参与网络功能的同时，继续执行感知操作，但不 将感知信息发送到汇聚节点。因此，网络中会动态地产生通信空洞。需要强调的是，这些 空洞在性质上是动态的，不同于现有传感器网络中已知的空洞（例如Ahmed等人[2005] 和Yu等人[2007]）。这些空洞可能在网络运行过程中产生或消失，从而增加或减小网络中 空洞的规模。该问题具有研究意义，因为这种影响并非永久性的，而是临时的——当环境条 件恢复良好时，节点将恢复正常的操作。因此，这种行为被视为一种异常行为，并可能带 来不利影响

对网络性能的影响需要得到充分解决。通过调整单个节点的通信范围来重新建立大量 共处且断开连接的节点之间的连通性可能并不可取，因为该节点的能量会迅速耗尽，导致 其快速死亡。因此，应实现一种“平衡”，以最优地调整节点的通信范围，并激活部分选 定的休眠节点，从而使额外的能量消耗在各节点之间均匀分布，进而延长网络的寿命。由 于哑行为本质上是动态的，当有利环境条件恢复时，那些已增加通信范围的节点需要减小 其通信范围；而为重新建立连通性而被激活的额外节点则需要返回休眠状态，以减少网络 的额外能量消耗。

1.2.贡献

在本研究中，我们构建了一个使用可调范围传感器节点的网络，这些节点可以通过增加能 量消耗来调整其通信范围。在连通性重建过程中，依赖单个传感器节点并调整其通信范围 以重新建立连通性是不可取的。这样做会导致该节点的能量消耗加快，从而使其更早失效。 此外，每个节点的通信范围都有一个最大限制，即使将通信范围增加到该限制，也可能仍 无法重新建立连通性。因此，我们需要优化传感器节点通信范围的调整。为了平衡传感器 节点的能量消耗并延长网络寿命，需要进行额外的节点激活。我们在此项工作中的整体贡 献概述如下。

—我们提出一种名为CoRAD的基于价格的优化机制，用于在不利环境影响初期因通信范围 动态收缩而导致节点暂时孤立时，重新建立节点连通性。—当恢复有利环境条件时，需要 将增加的通信范围恢复至正常水平，并将额外激活的节点重新置为休眠状态。本文提出了 一种解决该问题的方案。—我们对所提方案CoRAD进行了理论表征。—我们进行了基于 仿真的性能评估，并与其他现有的拓扑管理协议进行了比较。

1.3.组织结构

本文其余部分组织如下。第2节描述了该领域的相关工作。第3节阐述了本文所解决的问题。 第4节和第5节分别对整个系统进行建模并提出针对该问题的解决方案。我们在第6节中描 述了仿真设置并对结果进行了分析。第7节给出了结论，并指出了未来可能的扩展方向。

2.相关工作

无线传感器网络中的一个关键问题是建立传感器节点之间的连通性，以便感知信息能够在 与其他节点协作的同时从源节点传输到汇聚节点。传感器节点之间的协作与合作是传感器 网络正常运行所关注的主要问题。通信范围缩小是影响这些网络中节点间成功协作的主要 挑战，进而会降低网络性能。Misra和Jain[2011]提出了一种用于无人值守无线传感器 网络的自组织和自愈的策略控制

自配置机制（PCSSN）方案，用于拓扑管理与维护。在该方案中，他们利用了密集部署的 传感器网络的冗余特性，仅激活那些能够降低网络能量消耗的节点。他们基于马尔可夫决 策过程（MDP）设计了节点激活策略，以激活最少数量的节点，同时不影响应用保真度。 在这些策略中，作者在构建和维护拓扑时未考虑由于通信范围缩小导致的节点孤立问题。 Zhang和Hou[2005]证明，为了实现完全覆盖和连通性，通信范围应为感知范围的两倍。 他们提出了一种完全去中心化和局部化的算法，称为最优地理密度控制（OGDC），用于 发现并激活一个最小子集的节点，以确保这些节点之间的覆盖和连通性。在他们的算法中， 作者未考虑由于恶劣环境条件导致的通信范围缩小，在这种情况下，节点可能无法满足该 约束条件。传感器节点的通信范围需要达到感知范围的两倍，因此在网络中可能无法提供 完全的覆盖和连通性。Khelifa等人[2009]开发了一种新的监控机制，以保证无线传感器 网络中的强连通性。在任意时刻，该机制都能检测代表网络连接监控关节点的关键节点。 这些关节点连接网络的不同部分。因此，开发了一种自组织机制，以提高其周围区域的连 通度，从而增强容错能力。Dini等人[2008]提出了一种修复分裂网络的方法。他们通过确 定移动节点的合适位置，重新建立传感器节点之间的连通性。然而，当无线传感器网络的 部署区域为非平面时，即存在障碍物干扰移动节点的移动，该方法可能无效。Senel等人 [2011]提出了一种基于蛛网结构的方法，借助最小生成树来重新连接因传感器节点损坏而 形成的分区网络。在此工作中，他们部署了中继节点以重新连接被分割的网络，这些中继 节点是永久部署的。然而，Khelifa等人[2009],、Dini等人[2008],以及Senel等人 [2011]的研究仅考虑了永久性的连接问题，并采取措施缓解永久性节点孤立问题。他们未 考虑由外部环境因素引起的临时节点隔离。

阿纳斯塔西等人[2004]展示了传感器节点的性能如何受到恶劣环境条件的影响。这些 条件会导致永久性或临时性的无线链路故障[帕拉迪斯和韩 2007]。此外，温度会影响无线 通信链路的信号强度以及传感器节点的传输功率[班尼斯特等人2008；纳迪姆等人2010； 博亚诺等人 2010]。法尼莫昆和弗罗利克[2003]以及米什拉等人[2011]研究了传感器网络 的连接问题。在他们的实验中，主要使用了低成本的环境感知网络。邦瓦赞等人[2011]采 用了一种两层次方法，基于生命周期评估（LCA）和能量建模来开发计算模型。他们首先 探讨了无线传感器网络基础设施及其生命周期，然后详细阐述了环境影响对评估模型的作 用。从现有文献的回顾可以看出，环境影响对传感器节点的通信具有不利影响，从而导致 通信范围缩小。

拉贾戈帕兰和瓦尔什尼[2009]研究了在存在信道衰落的情况下无线传感器网络的概 率连通性问题。他们建立了一个数学模型，用于评估传感器网络的概率连通性，该模型结 合了无线信道特性、多址干扰、网络拓扑和传播环境等因素。他们提出了一个分析框架， 用于计算在不同情况下的节点孤立概率和网络连通性

信道衰落模型。Ruiz等人[2004]提出并评估了一种基于无线传感器网络管理架构 MANNA的故障检测方案。该架构可为事件驱动的无线传感器网络提供自配置、自诊断和 自愈能力，以及部分自动化的自管理功能。Dhurandher等人[2009]基于服务质量（ QoS）和信誉机制考虑行为异常节点，以寻找用于路由的安全路径。在这些研究中，作者 将恶意外部实体的攻击、节点故障或功能失常视为传感器节点出现异常行为的主要原因。 然而，他们并未将由于不利环境影响导致通信范围收缩，从而使节点暂时无法向其他节点 发送其感知信息的行为视为异常行为，而Misra等人[2014],、Roy等人[2014a,2014b, 2014c],、Kar和Misra[2015],、Kar等人[2015],以及Jose等人[2011]则考虑了此类情 况。他们提出了可调传输范围（ART）协议，该协议根据传感器节点的位置并利用长距离 通信来平衡各节点之间的能量消耗。该协议通过减少较长跳数通信的数量，实现将信息路 由至基站。这是通过根据网络中节点的位置调整传输范围功率来实现的。Mao等人[2011] 通过选择和优先排序转发列表，最小化了无线传感器网络中将数据转发至汇聚节点的总能 耗。他们提出了高效节能机会路由（EEOR）方案，其中所有传感器节点的传输范围要么是 固定的，要么是动态可调的。然而，这些研究仅考虑了通信范围的永久性变化；为此，它 们通过调整通信范围以建立节点间的连通性，但未考虑因环境的临时性变化而需要调整通 信范围的情况。

综合：对现有文献的回顾表明，作者研究了不同类型的异常行为、故障、连接问题以 及环境影响。S.米斯拉等人[2014]研究了在恶劣环境条件下传感器节点出现的一种行为， 并将其称为哑行为。他们对该行为在无线传感器网络性能上的影响进行了表征和分析。事 实上，由于哑行为对网络性能具有负面影响，因此可将其归类为一种特定类型的异常行为。 Roy等人[2014a,2014b,2014c],、Kar和Misra[2015],以及Kar等人[2015]评估了 存在哑节点时无线传感器网络的性能，并提出了多种针对这些节点的检测方案。然而，在 现有文献中，尚无用于将暂时孤立的哑节点重新连接至网络的方案。在本研究中，我们利 用可调通信范围的传感器节点，重新建立网络中孤立节点之间的连通性，以改善其下降的 网络性能。

3.问题描述

哑行为[Misra等 2014]是由于雾、降雨和高温等环境现象突然发生而引起的。如果由于 这些现象导致传输范围缩小，则节点在某些时刻可能能够感知其物理环境，但无法与其邻 居进行通信。

我们考虑了网络中的两种节点：(a)正常行为的节点和(b)哑的节点。此外，所有传感 器节点都被视为非均匀的，这意味着每个节点具有相同的感知能力，但可以调整其通信范 围。表I列出了本文中使用的所有符号。

设R为传感器节点的固定通信范围。在图1中，设dmin[Misra等 2014]为节点X到其最 近的活跃邻居节点Y的距离。我们有
$$
dmin= min(r ne c) ∀ne. (1)
$$

表I.本文中的符号说明 符号 描述
n 节点的正常行为
d 节点的哑行为
rcne 节点到活跃邻居节点的通信范围
dmin到最近的活跃邻居节点的距离
ne 活跃邻居节点列表
R 传感器节点的最大指定固定通信范围
rc(t) 在时间t的通信范围
Er i 邻居节点ni的剩余能量
Emr 最大剩余能量
Rl i 邻居节点ni的接收信号强度
Rlm 最大接收信号强度
ϕi 节点ni到连接BEGIN和STOP节点的直线的距离
υi 节点ni与STOP节点之间的距离
Luv BEGIN和STOP节点对之间的距离
De i 节点ni的有效距离
Hc i 节点ni到BEGIN节点的跳数
Hc m 最大跳数
e i 节点ni的能量等级
e m 节点的最大能量水平
ωi 节点ni的价值函数
ςi 节点ni的成本函数
σi 节点的选择约束ni
bi 节点的效益函数ni
bc i 节点ni的累积收益
trep 接收REPLY数据包的估计时间
trpt 重复算法的估计时间

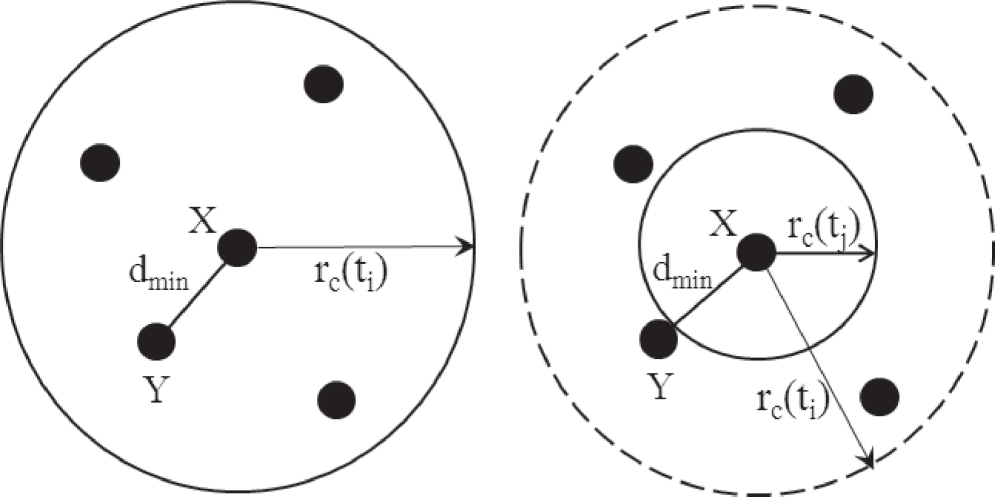
定义1.正常行为 ：一种能够在周围环境中感知物理现象，并在其整个生命周期内传输 感知数据的传感器节点被称为正常行为节点（参见图1(a)）。此类行为用n表示。数学上[ Misraetal. 2014],
$$
n={1, (0< dmin ≤ rc(ti) ≤ R) ∀ti
0, otherwise . (2)
$$

定义2. 哑行为 ：一种传感器节点，能够感知其周围环境中的物理现象，但在某一特定时刻无法 传输所感知的数据

由于存在温度、雾或降雨等恶劣环境条件，但能够在环境条件恢复有利时在不同时间点进 行传输的节点被称为哑节点[Misraetal. 2014]（参见图1(b)）。这种行为用d表示。 数学上[Misraetal. 2014],
$$
d={1, {(0< dmin ≤ rc(ti) ≤ R)} ∧{0 ≤ rc(tj)< dmin< R)} ∀ti, tj ti = tj
0, otherwise . (3)
$$

在公式(3)中，我们考虑任意两个时间点ti 和tj（其中ti = tj），如果满足该条件（方 程的第一行），则节点表现出哑行为；否则，节点行为正常。实际上，该方程表示了一个 节点在其生命周期内哑行为的暂时性。因此，我们考虑了所有的时间点ti 和tj。我们考虑 了两个不同的时间点ti 和tj，因为哑节点在不同时间点表现出不同的行为，即节点行为的 暂时性。

由于哑节点引起的拓扑变化：由于不利环境影响的存在，传感器节点的通信范围缩小。 由于这种通信范围缩小，传感器节点可能会与网络失去连接而孤立。由于不利环境影响具 有时间性和变化性，通信范围的缩小也可能随时间而变化。因此，根据通信范围的缩小情 况，无线传感器网络中可能会出现链路中断、网络分割和节点孤立。

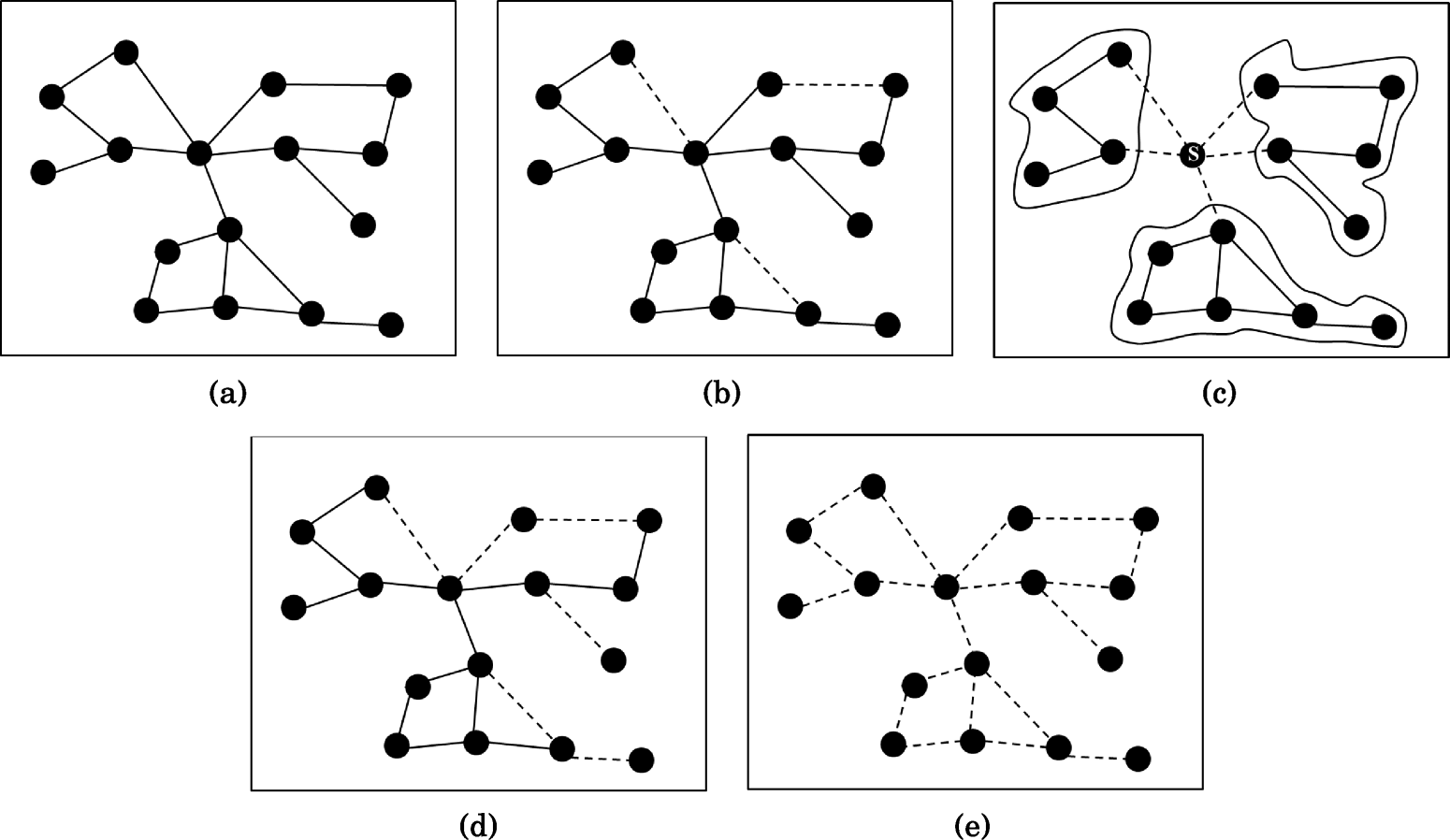
在正常条件下工作的无线传感器网络如图2(a)所示。它可以表示为一个图G=(N,L)， 其中N表示节点的集合，L表示节点之间的链路集合。 | N| = κ是网络中节点数量。汇聚节 点表示为s ∈ N。根据传感器节点通信范围缩小的情况，不利环境因素的影响可分为以下 几种情况：

Case 1 ：在存在中等程度不利环境影响的情况下，通信范围的收缩并不严重。因此，网络中的 少量链路断裂，但

使整个网络仍然保持连通，如图2(b)所示。该场景可以数学上定义为 ∀n ∈N存在路径sn。 在这种情况下，由于网络是连通的，所提方案CoRAD无需在任何节点上执行。链路 断裂可能导致服务质量（QoS）下降。然而，在本研究中我们仅考虑孤立节点连通性的恢 复，而不考虑QoS的下降问题。

情况2 ：在静态无线传感器网络中，哑节点的出现不仅取决于通信范围的缩小，还取决 于节点活跃邻居的位置。在图2(c)中，当节点A在不利环境影响下通信范围缩小时，所有与 节点A的链路均中断（如虚线所示）。因此，节点A与网络隔离。于是，图2(a)所示的原始 网络分裂为三个部分（如图2(c)所示）。数学上，该场景可定义为：对于所有正整数κ1, κ2,. .., κp，使得∑ p i=1 κi= κ，存在N(G)的一个划分为 p个部分N1, N2,...,Np，使得 | Ni| = κi，且对每个{ii s}，N 1 ≤诱导出G的一个连通子图，并且N ≤是包含汇聚节点s的 特定子图，其中s s 1 ≤p。因此， ≤n ∀(N ∈Ni)，其中(iss)不存在路径sn。

我们考虑使用CoRAD来实现临时孤立节点与网络的连接。仅当节点从网络中孤立时， 才会调用CoRAD ；因此，无法在网络分区之间重新建立连通性。然而，在这种情况下， 孤立节点可通过CoRAD与网络重新连接。

情况3 ：由于存在不利环境影响，部分传感器节点与网络失去连接。在这种情况下， 孤立节点与汇聚节点之间不存在路径。图2(d)显示，由于通信范围缩小，导致部分节点发 生孤立。数学上， ∃n ∈N，使得不存在路径sn。

在此情况下，孤立节点可利用所提方案CoRAD.重新建立与网络的连通性。

情况4 ：由于存在极端恶劣环境条件，所有传感器节点彼此之间均被孤立。在这种情况 下，任意节点与汇聚节点之间均无路径。图2(e)显示，由于通信范围缩小，所有节点彼此 断开连接。数学上， ∀n w ∈ N时不存在路径nw，当n= w。

在这种情况下，由于所有节点彼此隔离，每个节点都需要启动连通性重建过程。

4.系统模型

这项工作基于由于传感器节点存在哑行为而导致的节点孤立问题。由于哑行为本质上是暂 时的，因此节点孤立也是暂时发生的。在此项工作中，我们的目标是重新建立孤立节点与 网络之间的连通性。为此，我们提出了一种方案CoRAD，利用可调节的传感器节点来实现 该目标。我们假设无线传感器网络部署在无障碍区域，因此在这种场景下，对数距离路径 损耗信道模型[Seybold 2005]是适用的。在此路径损耗模型中，发射功率、接收功率以及 发射器与接收器之间距离的关系[Levis 2005]如下：
$$
PR= PT GRGT( λ 4πd)^η
(4)
$$
其中，PT和PR分别为发射功率和接收功率；GT和GR分别为传输天线增益和接收天线增益； λ是

波长；以及d表示一对节点之间的距离。 η是路径损耗指数，取决于介质的衰减效应。在 自由空间中， η的值为2，但在存在恶劣环境条件时，其值可高达8。随着 η值的增加，接 收功率降低。因此，传感器节点发射的信号相比理想情况会在更短的距离内达到其接收阈 值。因此，通信范围与信号的接收功率成正比，在存在恶劣环境条件时，通信范围会减小。

定义3.起始节点 ：一个起始节点U是一个孤立节点，它启动CoRAD以与终止节点连接。 传感器节点的通信范围在存在不利环境影响的情况下会减小。此后，开始节点可以激 活位于其当前（减小的）通信范围内的休眠邻居节点。当在当前（减小的）通信范围内不 存在任何休眠邻居节点时，开始节点能够调整其通信范围以寻找任意邻居节点。

定义4.终止节点 ：一个终止节点V是某个起始节点U的连接节点，该起始节点此前与 之相连，但在当前时刻已断开连接。CoRAD方案在此节点上停止执行，并选择一条从该 节点到U的可靠且最优路径。

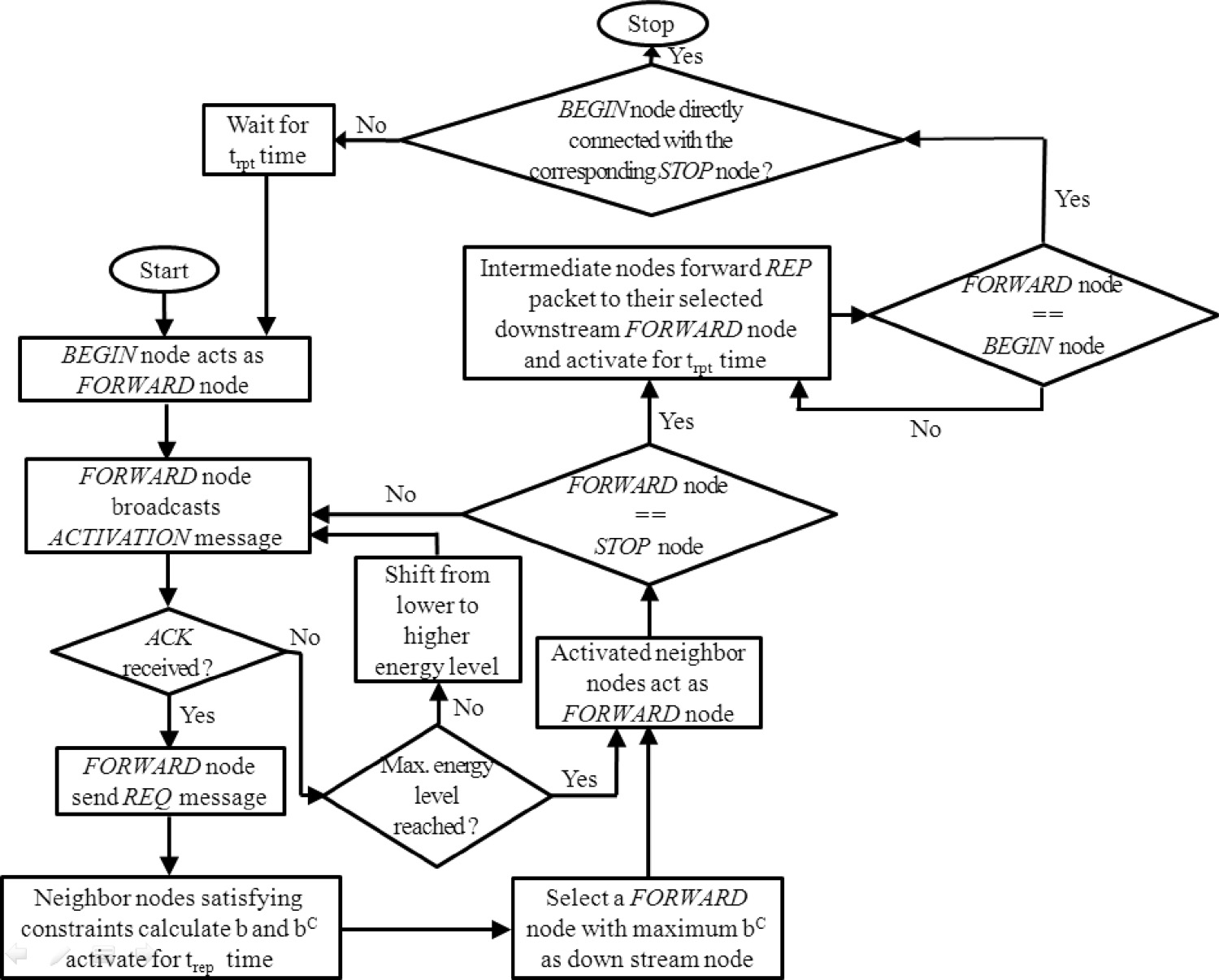
每个STOP 节点都有其对应的BEGIN 节点，该节点是一个孤立节点。BEGIN 节点尝试在自身与 STOP 节点之间重新建立连通性。CoRAD 方案从一个BEGIN 节点开始，在STOP 节点结束。

定义5.转发节点 ：转发节点计算自身的常规收益和累积收益值。此外，它将连通性重 建过程向终止节点转发。最后，根据最高的累积效益值选择一个下游转发节点。

FORWARD节点是位于一对开始和停止节点之间的中间实体。它在计算自身的常规 收益和累积收益后，将连通性重建过程转发给上游邻居节点。如果一个FORWARD节点无 法在其当前（已减小的）通信范围内找到任何邻居节点，则会调整其通信范围。

所提出的基于价格的分布式方案激活了开始节点和停止节点之间的一组最优中间休眠 节点子集。在少数情况下，当开始节点和停止节点之间的中间节点数量不足时，该方案还 会重新调整中间节点或开始节点的通信范围，以重新建立连通性。

设 P表示参与者集合，即P={ρ1, ρ2, ρ3,…, ρn}。效益函数的集合记为 B，其中 B={bρ | ρ ∈ P}。因此，我们将基于价格的方案定义为 ξ= 〈P, B〉。

一些支持GPS的可调通信范围传感器节点被随机部署在某个感兴趣的区域。最初，所 有传感器节点均处于激活状态。然而，在能量受限的无线传感器网络中，长时间保持所有 传感器节点激活是不可取的，因为这会导致传感器节点不必要地消耗能量，并产生冗余覆 盖。因此，应激活一个最小子集的传感器节点，以实现对整个区域的最优覆盖。由于不利 环境影响的发生，传感器节点的通信范围会缩小。如果某个节点的通信范围缩小至低于其 最近的活跃邻居节点的距离，则该节点将与网络发生孤立。这种孤立是暂时的，当恢复到 有利环境条件时，该节点将恢复正常行为并重新连接到网络。

与网络连接。当传感器节点检测到自身与网络隔离时，它将启动所提出的CoRAD方案， 在开始和停止节点之间重新建立连通性。

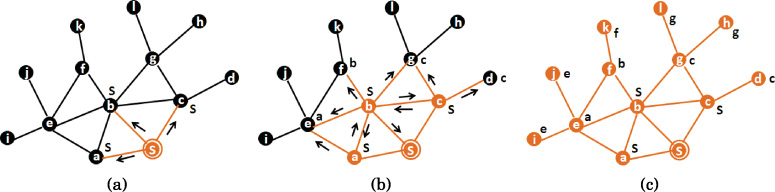
初始部署后，所有激活的传感器节点都会寻找其连接节点。如果所有传感器节点都保持 与其连接节点的连接，则可确保网络完全连通。具体而言，所有传感器节点与其连接节点的 连通性至少保证了从每个节点到汇聚节点的一条路径。开始时，汇聚节点广播一个HELLO 消息。单跳邻居节点在接收到HELLO消息后，选择汇聚节点作为其连接节点。随后，这些 邻居节点广播一个HELLO消息。当单跳邻居节点接收到HELLO消息后，若尚未选择任何连 接节点，或者其本身不是汇聚节点，则选择第一个向其发送HELLO消息的节点作为其连接节 点。该过程逐步在网络中的其他节点中进行，直到所有节点都选择了各自的连接节点。连接 节点选择过程如图3所示。

所提方案的目标是重新建立BEGIN和STOP节点之间的可靠连通性。为了重新建立 连接，所提CoRAD方案会激活最优数量的中间休眠节点。当某个节点的减小的通信范围内 没有休眠邻居节点时，需要调整该特定节点的通信范围。类似地，如果BEGIN节点在其减 小的通信范围内没有任何邻居节点，则需调整其通信范围。剩余能量Er i是影响传感器网络 中节点ni可靠性的一个重要参数。链路质量是影响网络中节点间连通性的一个重要参数。 具体而言，接收信号强度（RSS）是节点之间可靠通信的重要链路质量度量指标。较高的 RSS表示更优的链路质量。节点ni的RSS表示为 Rl i。此外，为了降低网络的整体能量消耗， 还需要激活较少数量的节点来重新建立BEGIN和STOP节点之间的连通性。为了实现激活 更少数量的节点，我们引入另一个参数，即有效距离De i，如下所示。
$$
De i= ϕi+ υi. (5)
$$

在公式（5）中， ϕi是节点ni与STOP节点V之间的距离； υi是节点ni到连接 BEGIN和STOP节点的直线之间的距离，如图4所示。这两个参数的求和用于推导有效距 离De i，因为激活较少数量的节点需要进行选择

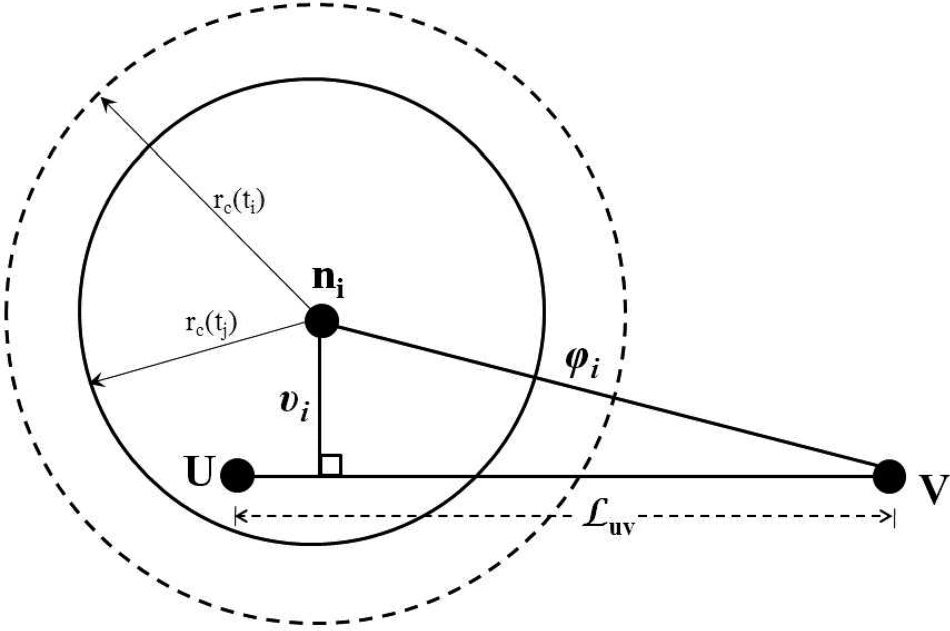
距离STOP节点最近且最接近连接BEGIN和STOP节点的直线的节点。因此，当 ϕi和 υi 均为最小时，有效距离De i最小。我们试图对距离ϕi和 υi赋予同等的重要性。我们根据节点 在连通性重建过程中的参与度为其分配重要性。在特定情况下，若某节点的有效距离较大， 则该节点获得的重要性较低，反之亦然。因此，为了激活参与连接恢复过程的节点，我们 考虑其有效距离。此外，有效距离被纳入效益函数中，并基于最高的累积效益值来寻找整 体最优路径。从BEGIN节点到某节点的跳数被视为另一个参数。选择跳数较少的可靠路径， 因为这可以减少节点激活次数。我们将节点ni的跳数记为 Hc i。为了调整传感器节点的通信 范围，发射器具有不同的能量等级。通常，传感器节点在最低能量等级下运行。当节点需 要增加其通信范围时，会以额外的能量消耗为代价，从较低能量等级切换到较高等级。所 提方案的目标是使传感器节点ni的能量等级e i保持在较低水平。

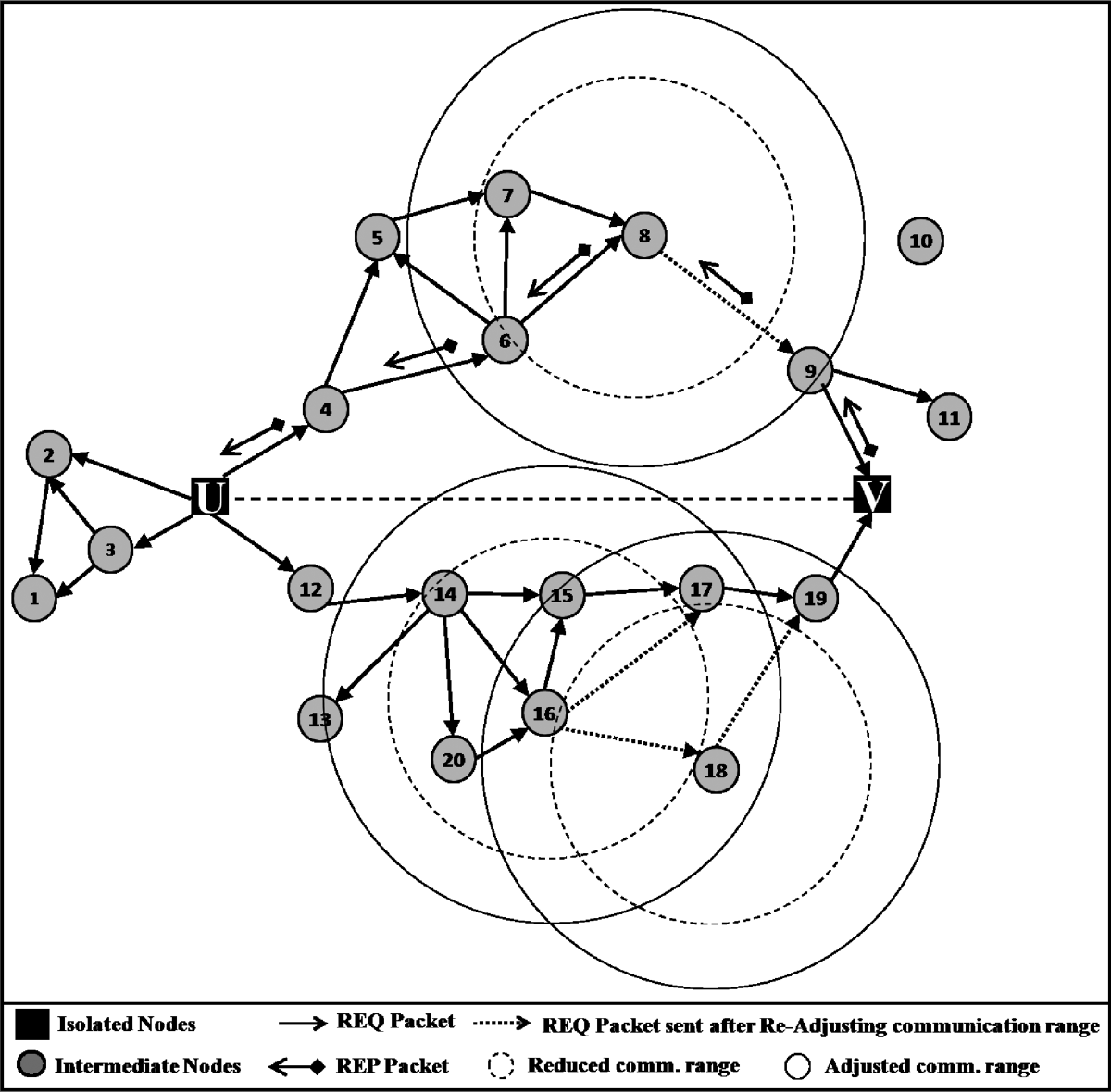
假设部署了 κ个传感器节点，每个节点被分配唯一的ID，使得id={1… κ}。由于恶劣环 境条件的发生，如果一个传感器节点与网络隔离，它将开始作为BEGIN节点，并启动连接恢复。 当该节点此前与BEGIN节点相连但已断开连接时，BEGIN节点会与最近的已激活邻居节点—— 即STOP节点重建连通性。图6展示了BEGIN节点U如何与STOP节点V重建连接。初始时， BEGIN节点充当FORWARD节点，激活其邻居节点并使其参与连接恢复过程。随后，已激活 的邻居节点轮流担任FORWARD节点，逐步推进连接恢复过程，直到STOP节点成为 FORWARD节点。当前的FORWARD节点在其单跳邻居范围内广播节点ACTIVATION消息，以 唤醒处于休眠状态的邻居节点。收到ACTIVATION消息后，那些尚未作为此特定BEGIN节点的连 接恢复过程中的FORWARD节点且满足选择约束的邻居节点，将回复一个ACK数据包。如果 FORWARD节点未收到任何ACK，则从较低能量等级切换到较高等级以增加其通信范围，并重 复该过程直至接收到任意A κ。若在最大能量级别仍未收到任何A{v2}，则无法参与连接恢复过 程。A{v3}消息包含转发节点ID（FWD={1… κ}ID）和广播地址（ BROADCAST{v5}ADDR）。A{v6}消息包含邻居ID（NBR{v7}ID）和邻居地址（ NBR{v8}ADDR）。A{v9}和A{v10}数据包的格式分别如图5(c)和图5(d)所示。

节点U发起连接恢复过程并作为转发节点。它在其减小的通信范围内向节点2、3、4和12广 播ACTIVATION消息。在收到来自邻居节点的ACK后，节点U向节点2、3、4和12发送R EQUEST数据包。REQUEST数据包包含起始节点ID（BGN_ID）、起始节点位置（BGN_ POS）、转发节点地址（FWD_ADDR）、终止节点ID（STP_ID）、终止节点位置（ STP_POS）、累积效益值（BNF_VAL）和跳数（HC），如图5(a)所示。接收到REQUEST 数据包的节点将在接下来的trep时间内保持活跃，并计算自身的效益值和累积效益值。参数 trep是预计从终止节点接收到REPLY数据包的时间。此后，每个接收到REQUEST数据包的节点都作为转发节点继续执行相同的过程，直到到达终止节点。根据最高的累积效益值，从 多个转发节点接收到REQUEST数据包的节点将选择其中一个转发节点作为通往起始节点的 下游节点。图6显示，节点8在扩大其通信范围（以虚线表示）后向上游节点9发送REQUEST 数据包，因为在减小的通信范围内没有其他节点可到达终止节点。类似地，节点16和18也 扩大其通信范围以获得邻居节点。当终止节点从多个转发节点接收到REQUEST消息时，会 选择其中一个作为通往起始节点的下游节点，并向其发送REPLY数据包。REPLY数据包包含 终止节点ID（STP_ID）、终止节点地址（STP_ADDR）、起始节点ID（BGN_ID）和起 始节点地址（BGN_ADDR），如图5(b)所示。

5.提出的解决方案

我们提出了一种基于价格的[埃达拉特等人，2009年；刘和克里希纳马查里 2006]方案， 以重新建立孤立节点与网络的连通性。该所提方案通过激活一组最优的中间休眠节点，或 在通信范围内没有邻居节点时增加传感器节点的通信范围，从而可靠地重新建立孤立节点 与网络的连接。该基于价格的解决方案是根据剩余能量Er、接收信号强度Rl、有效距离 De、 跳数 Hc以及能量等级 e设计的。

无线传感器网络被建模为一个图G(N,L)，其中每个节点ni ∈ N和 ∀lij ∈ L
与 ∀lij ∈ L，其中lij 是任意节点ni与nj之间的链路，i ≠ j。为了重新建立每对节点之间的连通性，一个开始节点尝试与一个停止节点建立连接，其余节点则作为中间节点。根据基于价格的方法，每个 节点ni满足一个约束条件（后文讨论），并按如下方式计算其自身的效益值：
$$
bi=(ωi − ςi), (6)
$$

其中bi、ωi和 ςi分别是每个节点ni、i ∈ κ的效益、价值和成本函数。

价值函数ωi对选择节点ni进行连接恢复的优势进行量化。该价值函数以E r和Rl作为参 数，因为具有更高剩余能量和接收信号强度的节点在连接恢复方面是比其他节点更优的选 择。因此，价值函数ωi设计如下：
$$
ωi=(Er m + Rl i Rl m) , (7)
$$
其中Er m和R l m分别为最大剩余能量（即初始能量）和最大接收信号强度。

成本函数ςi量化了选择相应节点ni的不利性。该成本函数考虑了参数D e、Hc和 e，因 为具有更大有效距离、跳数和更高能量水平的节点在连接恢复方面相比其他节点是较差的 选择。在设计成本函数之前，有必要先确定节点ni的有效距离。

设开始、停止以及任意中间节点ni的位置分别为(xu,yu)、(xv,yv)和(αi, βi)。连接开始和 停止节点的直线方程为：
$$
(yv −yu)x+(xu −x v)y+(xvyu −xuyv)= 0. (8)
$$

由方程(8)可知，节点ni到连接开始和停止节点的直线的距离 υi为：
$$
υi=|(yv −yu)αi −(xv −xu)βi+(xvyu −xuyv)|
√(yv −yu)2+(xu −xv)2 . (9)
$$

从STOP节点到节点ni的距离ϕi为：
$$
ϕi= √(xv − αi)2+(yv − βi)2. (10)
$$

BEGIN和STOP节点之间的距离Luv计算如下：
$$
Luv= √(xv −xu)2+(yv −yu)2. (11)
$$

因此，由方程(5)、(9)和(10)可得，节点ni的有效距离 De i为：
$$
De i= |(yv −yu)αi −(xv −xu)βi+(xvyu −xuyv)|
√(yv −yu)2+(xu −xv) 2 +√(xv − αi)2+(yv − βi)2. (12)
$$

成本函数ςi设计如下：
$$
ςi=(De Luv + Hc i Hc m + e i e m) . (13)
$$
参数Hc m和 e m分别是节点ni的最大跳数和最大能量等级数。

因此，效益函数bi对选择节点ni进行连接恢复的有效优势进行了量化。由方程(6)、(7)和(13)可得效益函数bi如下：
$$
bi= σi[ρ+(Er m + Rl i Rl m) −(De i Luv + Hc i Hc m + e i e m)] , (14)
$$
其中，σi 是节点ni的选择约束。该选择约束定义如下：
$$
σi= ⎧⎨⎩ 1,(Er th ≤ Er i ≤ Ei m) ∧(Rl th ≤ R l i ≤ R l m) ∧(0 ≤ ϕi ≤ Luv) 0, otherwise , (15)
$$
其中， Er th和 Rl th分别为剩余能量和接收信号强度的最小通信阈值。由于效益值必须为非负， 因此在方程(14)的效益函数中加入了一个常数 ρ。 ρ的值由引理5.3推导得出。

每个节点ni通过将其自身的效益值与从自身到开始节点的所有下游节点的总效益值相 加，来计算其累积效益值（bc i），如下所示：
$$
bc i= bi+ i−1 ∑ j=1 bj . (16)
$$

LEMMA 5.1 .一对起始节点和终止节点的最大有效距离De为2Luv 。

PROOF 。从公式（15）给出的约束可知，所提方案CoRAD受到距离约束0 ≤ ϕ i ≤Lu v 的限制，该 约束仅允许那些节点

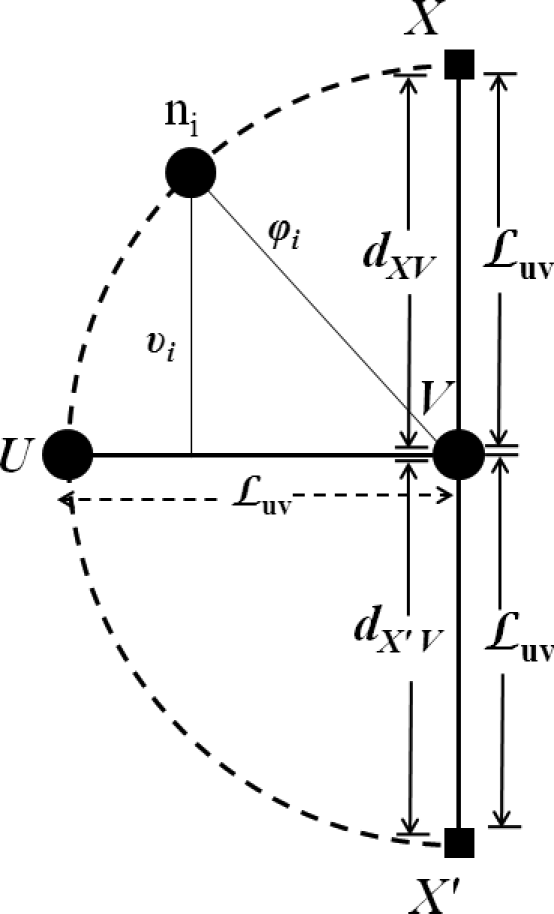
参与的节点位于以STOP节点V为中心的半圆X − U −X′内，如图7所示。当 ϕ和 υ均达 到最大值时，有效距离 De达到最大。这种情况可能出现在位于X和X′的节点上，其中 ϕ= υ= Luv。在这种情况下， De取得最大值，即：
$$
De= ϕ+ υ = Luv+ Luv = 2Luv. (17)
$$

THEOREM 5.2 .方程(14)中的效益函数具有最大值和最小值，如下所示：
$$
bi max= ρ+ 2 − 1 N −2 . bi min= ρ+ Er th Er m + Rl th Rl m −4,
$$
当Er th ≤ Er i ≤ Er m、 Rl th ≤ R l i ≤ R l m、 0 ≤ ϕi ≤ Luv和 σi= 1时。

PROOF 。方程(14)中的效益函数bi是 Er i、 Rl i、 De i、H c i和 e i的线性组合，当 σi= 1时成 立。该函数通过从价值函数ωi中减去成本函数 ςi而设计得到。当价值函数取得最大值且成本 函数取得最小值时，效益函数取得最大值。价值函数在Er i= Er m和 Rl i= Rl m时取得最大值。 因此，价值函数的最大值为：
$$
ω max i=(E r m Er m + Rl m Rl = 2. (18)
$$

当节点ni为停止节点，且无中间节点，同时传感器节点无需进行功率等级切换时，成本函 数的值最小。即Die= 0、Hic= 1和ie= 0。因此，成本函数的最小值为：
$$
ςimin=( 0 Luv + 1 N −2+ 0 me) = 1 N −2. (19)
$$

因此，效益函数的最大值为：
$$
bimax= ρ+ωim ax− ςmin = ρ+ 2 − 1 N −2. (20)
$$

当价值函数取得最小值且成本函数取得最大值时，效益函数取得最小值。当Er i= Er th和 Rl i= Rl th时，价值函数取得最小值。因此，价值函数的最小值为：
$$
ωmin i=(Er th Er m + Rl th Rl m) . (21)
$$

当 De i= 2Luv、 Hc i= Hc m和 e i= e m时，成本函数的值最大。因此，成本函数的最大值为：
$$
ςimax=(2Luv + Hc m Hc m + e m e =(2+ 1+ 1) = 4. (22)
$$

因此，效益函数的最小值为：
$$
bmin i= ρ+ωim ax− ςmin = ρ+(Er th Er m + Rl th Rl m) −4. (23)
$$

LEMMA 5.3 .方程(14)中 ρ的值为[4 −( Er th Er m + Rl th Rl m )].

PROOF 。为了获得正值效益，需要添加一个常数，将最小效益值调整为0。这样，从方 程(14)得出的所有效益值均为正值。方程(23)给出了最小效益值。在该方程中，如果我们代 入ρ=[4 −( Er th Er m + Rl th Rl m )],，则最小效益值变为0。
$$
bmin i= ρ+(E r th Er m + Rl th Rl m) −4 = 4 −(E r th Er m + Rl th Rl m) +(E r th Er m + Rl th Rl m) −4 = 0.
$$
由于Er th、 Er m、 Rl th和 Rl m是常数，因此 ρ也是一个常数。 因此， ρ=[4 −( Er th Er m + Rl th Rl m )]。

LEMMA 5.4 .方程(14)中的效益函数在区间Etrh ≤ Eir ≤ Emr, Rlth ≤ Rli ≤ Rlm, 0 ≤ Die ≤ 2Luv, 0 ≤ Hci ≤ Hmc和 0 ≤ie ≤me上是连续的。

PROOF 。多元函数y= f(x,y)在任意点(x0,y0)处是连续的，如果
∀ε> 0 ∃δ(ε)> 0, such that |x −x0| < δ, |y −y0| < δ ⇒ ∣∣f(x,y)− f(x0,y0)∣∣< ε.

方程(14)中给出的效益函数为：
$$
bi= σi[ρ+(EEmirr + RRlmli) −(LDuiev + HHmcci + ie me)] ,
$$
其中σi为常数。该函数在任意点(Er 0,R l 0,D e 0,H c 0, e 0)处连续。当 ∀ε> 0 ∃δ(ε)> 0时，令 |Er i −Er 0| < δ, |Rl i −R l 0| < δ, |De i −D e 0| < δ, |Hc i −H c 0| <δ和 |e i −e 0| < δ；则有 | f(Er i, Rl i,D e i,H c i, e i) −f(Er 0,R l 0,D e 0,H c 0, e i)| < ε，其中 δ和 ε为正常数。此外，σi在 Er th ≤ Er i ≤ Er m, Rl th ≤ Rl i ≤ Rl m, 0 ≤ De i ≤ 2Luv, 0 ≤ Hc i ≤ Hc m和 0 ≤ e i ≤ e m的 区间内也是一个正常数。因此，
$$
|bi − b0| = ∣ ∣ ∣ σi{ρ+(Er Eme + Rl i Rlm) −(De i 2L+ Hc i Hmc + e i me)} − σi{ρ+(Er 0 Ee m + Rl 0 Rl m) −(De 0 2L+ Hc 0 m + e 0 e m)} ∣ ∣ ∣ ∣ ∣ ∣ σi Er m) (Er i −Er 0)+( σi Rl m) (Rl i −R l 0) −( σi 2L)(De i −D e 0) −( σi Hc m) (Hc i −H c 0) −( σi e m) (e i −e 0) ∣ ∣ ∣ ∣ ≤ ∣ ∣ ∣ ∣ σi Er m ∣ ∣ ∣ ∣ ∣ r 0 ∣ ∣ ∣ ∣ ∣ σi Rl m ∣ ∣ ∣ ∣ ∣ l i −R l 0 ∣ ∣ + ∣ ∣ σi 2L ∣ ∣ ∣ ∣ e i −D e 0 ∣ ∣ ∣ ∣ ∣ σi Hc m ∣ ∣ ∣ ∣ ∣ c i −H c 0 ∣ ∣ ∣ ∣ ∣ σi e m ∣ ∣ ∣ ∣ ∣ ∣ e i −e 0 ∣ ∣ < ε. (24)
$$
Only if
$$
∣ ∣ ∣ ∣ σi Er m ∣ ∣ ∣ ∣ ∣ r 0 ∣ ∣≤ ε 5 , ∣ ∣ ∣ ∣ σi Rl m ∣ ∣ ∣ ∣ ∣ l i −R l 0 ∣ ∣≤ ε 5 , ∣ ∣ ∣ σi 2L ∣ ∣ ∣ ∣ e i −D e 0 ∣ ∣≤ ε 5 , ∣ ∣ ∣ ∣ σi Hc m ∣ ∣ ∣ ∣ ∣ c i −H c 0 ∣ ∣≤ ε 5 , ∣ ∣ ∣ ∣ σi e m ∣ ∣ ∣ ∣ ∣ ∣ e i − e 0 ∣ ∣≤ ε 5 (25)
$$
if ∣ ∣E r 0 ∣ ∣ ≤ ε 5 ∣ ∣ ∣ ∣ Er m σi ∣ ∣ ∣ ∣ , ∣ ∣R l i −R l 0 ∣ ∣ ≤ ε 5 ∣ ∣ ∣ ∣ Rl m σi ∣ ∣ ∣ ∣ , ∣ ∣ De i −D e 0 ∣ ∣ ≤ ε 5 ∣ ∣ ∣ ∣ 2L σi ∣ ∣ ∣ ∣ , ∣ ∣ Hc i −H c 0 ∣ ∣ ≤ ε 5 ∣ ∣ ∣ ∣ Hc m σi ∣ ∣ ∣ ∣ , ∣ ∣ e i − e 0 ∣ ∣ ≤ ε 5 ∣ ∣ ∣ ∣ e m σi ∣ ∣ ∣ ∣ . (26)
$$
Let
$$
δ1= ε 5 ∣ ∣ ∣ ∣ Er m σi ∣ ∣ ∣ ∣ , δ2= ε 5 ∣ ∣ ∣ ∣ Rl m σi ∣ ∣ ∣ ∣ , δ3= ε 5 ∣ ∣ ∣ ∣ 2L σi ∣ ∣ ∣ ∣ , δ4= ε 5 ∣ ∣ ∣ ∣ Hc m σi ∣ ∣ ∣ ∣ , δ5= ε 5 ∣ ∣ ∣ ∣ e m σi ∣ ∣ ∣ ∣ (27)
$$
$$
δ= min(δ1, δ2, δ3, δ4, δ5). (28)
$$

因此，由方程(27)和(28)可知，对于每一个 ε> 0，都存在一个 δ(ε)> 0，使得当 | x −x0| < δ, | y −y0| < δ ⇒ |f(x,y) −f(x0,y0)| < ε时成立。因此，方程(14)中的效益函数是连续的。

5.1.连通性探索

所提方案在起始节点和相应终止节点因不利环境影响导致通信范围缩小而被隔离时，重新 建立两者之间的连通性。当起始节点检测到自身与网络失去连接时，将发起连接恢复过程。 在连接恢复过程的初始阶段，起始节点作为转发节点，向其单跳邻居广播ACTIVATION消息。 邻居节点在接收到ACTIVATION消息后被激活。这些已激活的邻居节点中，若尚未参与过该 特定起始节点的连接恢复过程，并且满足公式（15）中定义的约束条件σi= 1，则向起始节 点回复ACK。当一个转发节点未从其邻居节点接收到ACK时，它将从较低能量等级切换到 较高等级，随后发送ACTIVATION消息并等待接收ACK。转发节点以相同方式持续进行，直到 收到来自其邻居节点的任意ACK为止。如果某个转发节点已达到最大能量级别但仍未能收 到任何ACK数据包，则禁止其继续参与连接恢复过程。满足约束条件的邻居节点将在接下来的trep时间内保持激活状态，其余邻居节点则进入休眠状态。参数trep是预计从终止节点 接收到回复数据包所需的时间。随后，起始节点向其邻居节点发送REQUEST数据包。每个 已激活的邻居节点利用公式（14）和（16）计算自身的效益值以及累积效益值（bc i）。该 过程在活跃邻居节点中继续进行。这些活跃邻居节点开始作为转发节点，向其所有邻居发 送ACTIVATION消息。那些尚未为该特定起始节点和终止节点对担任过转发节点、但满足公 式（15）所给约束条件的邻居节点，将向相应的转发节点回传ACK，并在接下来的trep时间 内保持激活状态。同时，它们在接收到转发节点发来的REQUEST数据包后，也会计算自身 的常规收益和累积效益值。若某邻居节点从多个转发节点接收到REQUEST数据包，则根据 最高的累积效益值选择其中一个作为通往起始节点路径上的下游节点。此过程在邻居节点 中迭代进行，并逐步向前推进，直至到达终止节点。算法1给出了从起始节点到相应终止节 点的连通性探索过程。

5.2.路径选择

在从多个FORWARD节点接收到REQUEST数据包后，STOP节点基于最高的累积效益值， 从这些FORWARD节点中选择一个作为通往BEGIN节点的下游节点。随后，STOP节点 向其直接下游的FORWARD节点发送一个REPLY数据包。当中间节点接收到REPLY数据包 时，会将其转发给在连通性探测过程中基于最高累积效益值所选定的直接下游节点。该过 程持续进行，直到REPLY数据包到达相应的BEGIN节点。接收到REPLY数据包的节点建立 从BEGIN节点到相应STOP节点的连接。接收到REPLY数据包的中间节点将在接下来的t rpt时间内保持激活状态，其中trpt是重复执行所提出的连接恢复过程的估计时间。算法2描 述了该过程

从STOP节点到对应的BEGIN节点的路径选择过程。整体操作流程如图8所示。

整个过程包括节点之间多种类型（ACTIVATION、ACK、REQUEST和REPLY）的消息交换。 随着网络中节点总数的增加，节点之间交换的消息总数也随之增加。网络开销直接取决于 网络中交换的消息数量。因此，随着新连接的建立，开销也随之增加。

恶劣环境条件虽然是暂时的，但并不频繁，且在恢复到有利环境条件之前可能会持续 相当长的时间。在恶劣环境条件下，传感器节点的通信范围会发生缩小，导致传感器节点 暂时与网络隔离。当恢复到有利环境条件时，这些孤立的传感器节点会重新连接到网络。 因此，在恶劣环境条件下，临时节点隔离的持续时间可能并不短。传感器节点的计算能力 速度非常高，同时传感器节点使用射频（RF）信号进行通信，提供了高通信速度和较低的 传播延迟。因此，连接恢复所需的等待时间可以忽略不计。节点之间连通性的恢复对于防 止临时节点隔离期间的数据丢失至关重要。然而，在连接恢复的等待期间，通过利用传感 器节点中可用的缓冲空间，可以减少数据丢失的可能性。

算法1:连通性探索
Require:
—起始节点ID：起始节点的ID—步骤ID：终止节点的ID—(xu,yu)：起始节点的位置—(xv,yv)： 终止节点的位置—trep：期望从终止节点收到回复的时间—trpt：重复时间1:如果(ID= 起始 ID)那么2:(xf,yf) ←(xu,yu)3:bc ← 04:Hc ← 05:结束如果6:广播ACTIVATION消息7:如 果接收到ACK那么8:发送REQUEST数据包9:否则10:当未接收到ACK 时循环11:从低到高能量 级别转移12:如果达到最大能量级别则13:退出循环14:结束如果15:结束循环16:结束如果 17:如果(ID ≠ 步骤ID)且(接收到REQUEST)那么18:(α, β) ← 节点位置19:计算 Luv、 ϕ、 υi 和 De20:Er ←节点的剩余能量21:Rl ← 节点的接收信号强度22:如果((Er th ≤ Er ≤ Er m)且( Rl th ≤ R l i ≤ R l m)且(0< ϕ ≤ Luv))那么23:ρ= 4 −(Er th E rm+ Rl th R lm ) 转移参数24:b ←[ρ+(Er E rm+ Rl R lm) −( De L uv + Hc H cm+ e m)]25:如果(ID ≠ 起始ID)那么26:bc ← BNF值+ b27:如果(接收到相同 起始节点ID的REQUEST数量> 1)那么28:节点缓冲区 ←转发地址，其中bc最大29:BNF值 ← max(bc)30:结束如果31:如果(接收到相同起始节点ID的REQUEST数量= 1)那么32:节点缓冲 区 ←转发地址33:结束如果34:Hc ← Hc+ 135:结束如果36:(xf,yf) ←(α, β)37:激活节 点持续下一个trep 时间38:节点广播ACTIVATION 消息，后跟REQUEST消息39:结束如果40:结 束如果

PROPOSITION 1 。当网络中有N个节点时，CoRAD的最佳情况和最坏情况时间复杂度分别为 O(1)和O(N)。

PROOF 。CoRAD分为两部分：连通性探索和路径选择。在连通性探索过程中，在最佳情况下， 不存在

算法2：路径选择
要求：
— forward addr[]：主节点地址列表
—bnf val[]：效用值列表
1:如果((FWD ID= STP ID)&&(收到REQUEST))那么
2: bnf val[] ← BNF VAL来自REQUEST数据包
3:对于i执行= 1到bnf val.length
4:转发w地址[i] ←FWDADDR
5:结束循环
6:如果REQUEST收到的数量> 1那么
7: F WD ADDR ← f orward addr with max(bnf val)
8: else
9: F WD ADDR ← f orward addr
10: endif
11:发送REPLY至FWD ADDR
12:结束如果
13:如果((FWD ID ≠BGN ID)且接收到REQUEST)，则
14:如果(!timeout(trep)那么
15: FWDADDR ←FWDADDR来自节点缓冲区
16:转发REPLY到FWD地址
17:为下一个trpt 时间激活节点
18:结束如果
19:结束如果

任何处于减小的通信范围内的休眠邻居节点，BEGIN节点调整其通信范围。在此调整之后， BEGIN节点与STOP节点相连。因此，在这种情况下，路径选择过程的时间复杂度也是 O(1)，因为STOP节点可以直接将REPLY包发送给BEGIN节点。因此，CoRAD的最佳情 况时间复杂度为O(1)+ O(1)= O(1)。

另一方面，当连通性探索过程需要遍历网络中的所有节点才能到达STOP节点时，就 会出现最坏情况。在这种情况下，连通性探索过程需要O(N)时间。此时，所选路径应为平 均长度为O(N)的路径。因此，REPLY数据包从STOP节点传输到BEGIN节点需要O(N)时间。 因此，路径选择过程的时间复杂度为O(N)。因此，CoRAD的最坏情况时间复杂度为 O(N)+ O(N)= O(N)。

THEOREM 5.5 . CoRAD建立的最终连通性是一种均衡。

PROOF 。我们假设CoRAD已经找到了从一个开始节点U到一个停止节点V的连通性C =(nu, n1, n2,… ni,nj,…, nk,…, np, nv)。因此，该路径的累积效益值为：
$$
bc v = bv+ bu+ p ∑ j=1 bj . (29)
$$
通过反证法，我们假设该路径未达到均衡。其他不位于此路径上的节点也可能满足该约束。 因此，CoRAD会找到另一条路径C′=(nu, n1, n2,… ni, nl,…, nm,…, nq, nv)，从一个开 始节点U到一个停止节点V，使得q ≤p。该路径的累积效益值为：
$$
bc ′ v = b v+ bu+ q ∑ j=1 b j . (30)
$$

表II.仿真参数
| 参数|值|
| —|—|
| 节点数量|150–350|
| 仿真区域|500米 × 500米|
| 感知范围|50m|
| 初始剩余能量|1.5–2.0焦耳|
| 正常情况下的通信范围 通情信况范围的变化|110m|
| 由于收缩|85–30米|
| 通信范围的增加 每单位能量级移动|20m|

CoRAD探索了开始和停止节点之间所有可能的连通性，并选择累积效益值最高的连通性。 因此，bc v ≠ bc′ v，尽管q< p。否则，CoRAD选择C′作为开始和停止节点之间的连通性。 因此，CoRAD建立的连通性是一种均衡。

6.仿真结果

6.1.仿真设计

我们考虑了由于节点存在哑行为而导致传感器节点暂时孤立的情况。所提方案CoRAD 仅 在节点孤立期间重新建立连通性。为了对所提算法进行仿真，我们考虑在500米 ×500米的 区域内部署150至350个异构传感器节点。初始时，所有节点均处于活跃状态。部署后，一 部分传感器节点保持激活状态以最优地覆盖整个区域，其余传感器节点则转入休眠状态。 仿真中使用的数据包格式（ACTIVATION、ACK、REQUEST和REPLY）如图5所示。我们还假设 数据包的发送和接收消耗的能量为50纳焦/比特。节点的感知范围为50米，在正常场景下通 信范围为110米。为了模拟由于不利环境影响导致的通信范围收缩，我们将通信范围从85米 变化到30米，以5米间隔递减。仿真参数列表见表II。我们基于以下参数对所提算法 CoRAD 进行了评估。

—孤立节点百分比：网络中每100个节点存在的孤立节点总数。孤立节点百分比的计算公式 为 I N× 100，其中I为孤立节点数量，N为网络中的节点总数。
—激活节点百分比：网络中每100个节点的激活节点总数。激活节点百分比的计算公式为 A N× 100，其中A为激活节点数量，N 为网络中的节点总数。
—成功率：在网络中能够成功建立连接的孤立节点数量（C）与孤立节点总数（I）之间的 比率。成功率的计算公式为 C I。
—平均路径长度：在开始节点与相应的停止节点之间恢复的连通性的平均跳数。平均路径 长度的计算公式为χ C+ 1，其中 χ表示网络中为连接恢复而激活的节点数量，C表示能够 成功与网络建立连接的孤立节点数量。
—消息开销：在网络中所有孤立节点执行连通性重建过程所需交换的控制消息总数。消息 开销计算公式为NactSact+NackSack+N reqSreq+ NrepSrep，其中Nact、Nack、N req和Nrep 分别为ACTIVATION、ACK、REQUEST和 REPLY数据包，以及Sact、Sack、Sreq和Srep分别是ACTIVATION、ACK、REQUEST和REPLY数据包的大小。
—能量消耗：所有孤立节点与网络重新建立连接过程中执行操作所需的总能量。因此，能 量消耗是指传输和接收ACTIVATION、ACK、REQUEST和REPLY数据包所消耗的总能量。

我们将所提算法CoRAD与两种最近提出的现有拓扑管理方案——基于学习自动机的节能拓 扑控制（LETC）[Torkestani 2013]和分布式拓扑控制算法（A1）[Rizvi等人 2012]—— 在激活的节点数量、开销和能量消耗方面进行了比较。结果通过对30次运行在变化的拓扑 上取集合平均绘制而成。在所有图中，x轴表示通信范围，y轴表示不同的仿真参数。

6.2.结果与讨论

本节对所提方案CoRAD的仿真结果进行分析和讨论。图9展示了在不同节点数量下，随着 通信范围的变化，孤立节点百分比的变化情况。该图显示，随着通信范围的逐渐增加，网 络中孤立节点的百分比下降。当节点的通信范围增大时，其减小的通信范围内存在激活节 点的可能性也随之增加，因此孤立节点数量随通信范围的增大而减少。同时发现，网络中 节点总数的减少会导致孤立节点百分比上升。其可能原因是：当节点数量减少时，网络变 得更稀疏，已激活的邻居节点数量也随之减少，导致更多节点在其通信范围内无法找到任 何处于活跃状态的邻居节点。因此，随着网络中节点总数的减少，孤立节点数量增加。

不同节点数量下，为维持拓扑结构所需激活节点百分比随通信范围变化的情况如图10 所示。我们观察到，随着通信范围的增加，所需激活节点的百分比下降。通信范围的增加 减少了网络中的孤立节点数量，从而导致需要更多的节点激活来重新建立网络中孤立节点 的连通性。该图还表明，节点总数的减少会增加所需激活节点的数量。

网络中孤立节点连通性的重建。节点总数的减少会导致网络中孤立节点数量的增加。因此， 节点总数的减少会增加为重建网络中孤立节点连通性所需激活的节点数量。

图11描述了在网络中节点数量变化的情况下，BEGIN和STOP节点之间恢复连通性 的平均路径长度。从该图中我们观察到，随着通信范围的增加，平均路径长度减小。其原 因是由于不利环境影响的存在，所有中间节点的通信范围也以类似于孤立节点的方式缩小。 此外还发现，由于传感器节点在网络中的随机部署，平均路径长度随着网络中节点总数的 变化而随机变化。

图12展示了在不同节点数量下，传感器节点的通信范围对连接恢复成功率的影响。该 图表明，随着网络中节点总数的增加，成功率也随之提高。从该图中我们还可以观察到， 随着通信范围的增加，成功率也增加。节点总数及其各自通信范围的增加，也会增加邻居 节点的数量。因此，邻居数量的增加提高了孤立节点找到邻居节点以恢复网络连通性的概 率。该图还显示，当网络中节点数量超过150时，在通信范围超过65m时，成功率达到了1。 这是因为当通信范围达到65m或以上时，所有孤立节点都已与网络重新连接。

图13展示了在不同节点数量下，重新建立连通性的消息开销随通信范围变化的情况。 该图显示，随着节点总数的增加以及各自通信范围的减小，消息开销也随之增加。网络中 节点总数的增加会导致每个节点的邻居数量增多，从而增加了网络中ACTIVATION、ACK和 REQUEST数据包的数量。相反，通信范围的减小会增加网络中孤立节点的数量。因此，需 要更多的ACTIVATION、ACK和REQUEST数据包来重新建立更多孤立节点的连通性。从而导致 ACTIVATION、ACK和REQUEST数据包数量的增加，进而提高了网络中的消息开销。

图14展示了在不同节点数量下，随着通信范围变化的连接性恢复的能耗。该图显示， 随着节点总数的增加以及各自通信范围的减小，能量消耗随之增加。网络中节点总数的增 加导致每个节点的邻居数量增多，从而增加了网络中传输和接收的数据包数量。另一方面， 通信范围的减小会增加网络中孤立节点的数量。因此，为重新建立网络中孤立节点的连通 性，所需传输和接收的数据包数量也随之增加。数据包传输和接收次数的增加导致整个网 络的能量消耗上升。

图15展示了CoRAD与两种最近提出的现有拓扑管理方案LETC和A1在激活节点百分比 方面的比较。在图15(a)、15(b)和17(c)中，考虑的节点总数分别为150、250和350。从这些 图表中可以看出，在LETC和A1方案下，随着节点通信范围的减小，激活节点百分比也随之 下降。然而，使用所提出的CoRAD方案时，随着节点通信范围的减小，激活节点百分比反 而增加。其可能原因是，由于通信范围减小，传感器节点逐渐变为孤立节点，因此现有的 拓扑管理方案无法重建整个网络的拓扑结构。而CoRAD通过激活额外节点或调整节点的通 信范围来实现