统计学——离散概率分布和连续概率分布

1.离散概率分布

1.1 伯努利分布

伯努利实验：同样的条件下进行的相互独立的实验，特点是实验的可能结果只有两种。成功/失败。如果随机变量X是一次伯努利实验，则这个随机变量就符合伯努利分布。一次抛硬币就是典型的伯努利分布。

1.2 二项分布

二项分布：发生次数是固定的，感兴趣的是成功的次数。

二项分布的判断依据如下：

• 做某件事的次数（也叫试验次数）是固定的，用n表示。
• 每一次事件都有两个可能的结果（成功，或者失败）
• 每一次成功的概率都是相等的，成功的概率用p表示
• 你感兴趣的是成功x次的概率是多少。那么就可以用二项分布的公式快速计算出来了。

二项分布计算公式：
$$P(x)=C_n^x{p}^x(1-p{)}^{n-x}$$
二项分布的期望和方差如下：

期望$E(x)=np$
方差$D(x)=np(1-p)$

我们需要注意，当n为1时，就是伯努利分布；而当n很大的时候，二项分布的形状与正态分布类似，所以计算n很大的概率时，可以正态分布计算概率。而当p<0.25，n>20，np<5时，二项分布可以用泊松分布来计算概率。

1.3 几何分布

几何分布：需要知道尝试多次能取得第一次成功的概率，则需要几何分布。

几何分布判断依据如下：

• 每一次事件都有两个可能的结果（成功，或者失败）
• 每一次“成功”的概率都是相等的，成功的概率用p表示
• 进行x次尝试这个事情，取得第1次成功的概率是多大

几何分布和二项分布很像，但关注点不同，几何分布关注第一次成功的概率，而二项分布关注的是成功的次数。
几何分布的概率计算公式：
$$P(x)=(1-p{)}^{x-1}p$$

p为成功概率，即为了在第x次尝试取得第1次成功，首先你要失败（x-1）次。

几何分布的期望和方差：

期望$E(x)=\frac{1}{p}$
方差$$D(x)=\frac{1-p}{p^2}$$

当p一定时，x=1的概率最大，随着x的增加概率越来越小。而p=100%时，我们第一次就成功了，而p接近0时，基本上都不会成功。

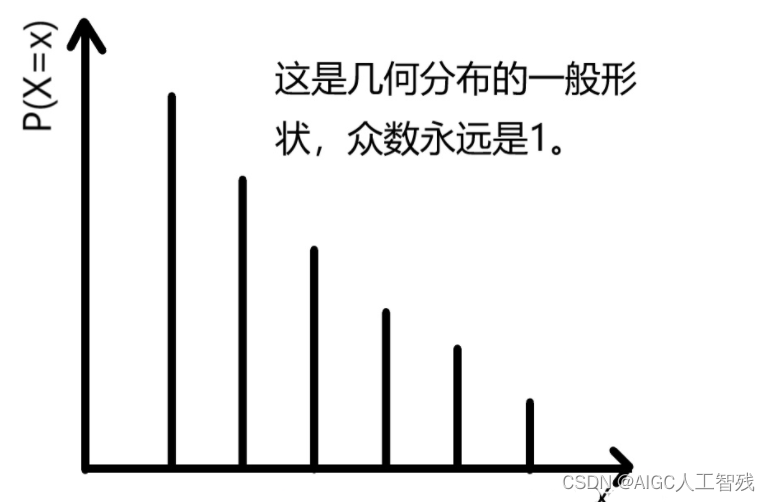
1.4 泊松分布

泊松分布：一定时间范围内某个事件发生的概率分布。泊松分布需要满足以下三个条件：

• 事件是独立事件
• 在任意相同的时间范围内，事件发生的概率相同
• 你想知道某个时间范围内，发生某件事情x次的概率是多大

如果你想知道某个时间范围内，发生某件事情x次的概率是多大。比如一天内中奖的次数，一个月内某机器损坏的次数，一段道路发生交通事故的次数等。
泊松分布计算公式：
$$P(x)=\frac{{\lambda }^x{e}^{-\lambda }}{x!}$$

• x代表你想要计算的事件次数，例如你想要计算一天内中奖7个人的概率，x就是7；
• λ代表中奖这个事件一天内发生的平均次数，注意跟x区别开来；

泊松分布的期望和方差：

期望$E(x)=\lambda$
方差$D(x)=\lambda$

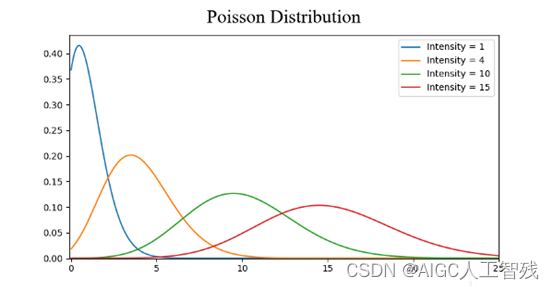
λ的大小会影响泊松分布的形状。当λ较小时，泊松分布向右倾斜；当λ增大时，泊松分布逐渐对称；而λ增大到一定程度时，泊松分布呈正态分布。如下图

2.连续概率分布

2.1 均匀分布

均匀分布：是关于定义在区间a,b上连续变量的简单概率分布，其概率密度函数如下图所示。

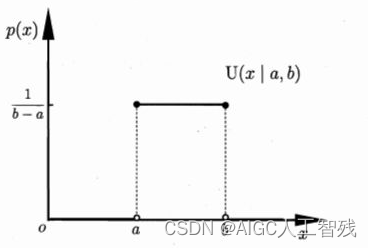
均匀分布的概率密度函数：
$$f(x)=\frac{1}{a-b}$$
数学期望和方差：

数学期望$E(x)=\frac{a+b}{2}$
方差$$D(x)=\frac{(b-a{)}^2}{12}$$

2.2 正态分布

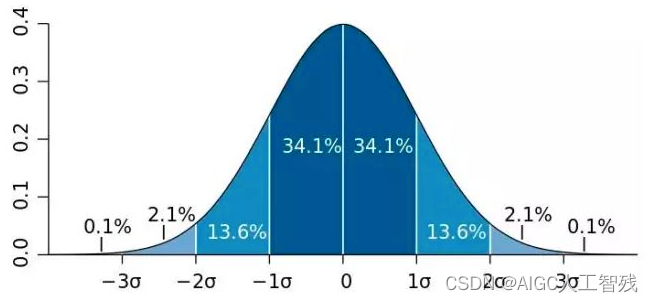
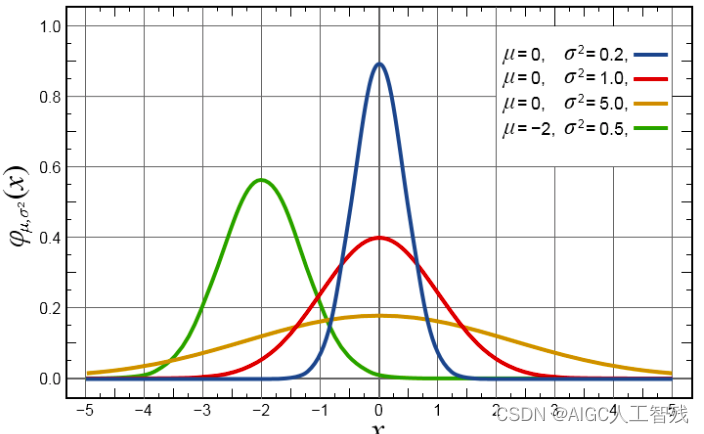
正态分布：连续型随机变量中最重要的分布。世界上绝大部分的分布都属于正态分布，人的身高体重、考试成绩、降雨量等都近似服从。正态分布如同一条钟形曲线。中间高，两边低，左右对称。大部分数据集中在某处，小部分往两端倾斜。如下图所示：

概率密度函数：
$$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
数学期望和方差:

数学期望$E(x)=\mu$
方差$D(x)={\sigma }^2$

均值μ表示正态分布的左右偏移，标准差σ决定曲线的宽度和平坦，标准差σ越大曲线越平坦。

正态分布性质：
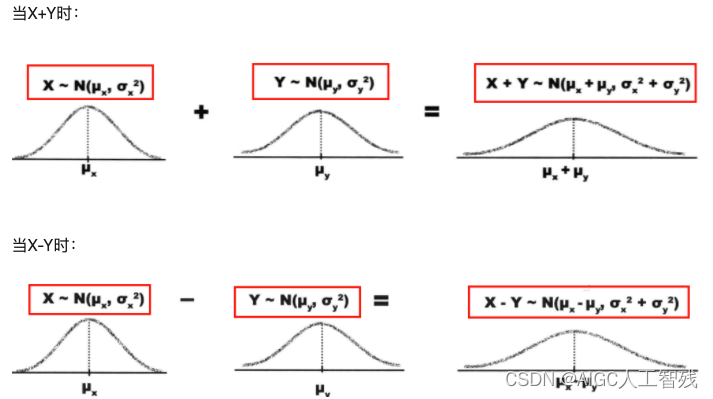
如果独立随机变量X和Y符合正态分布，那么X+Y也符合正态分布。如果正态分布X~N(μ, σ²)中，Y是一个线性变换的形式aX+b，因为X符合正态分布，所以aX+b也符合正态分布。

2.3 其他分布

• Z分布：就是标准的正态分布，普通的正态分布经过Z得分能够得到Z分布；

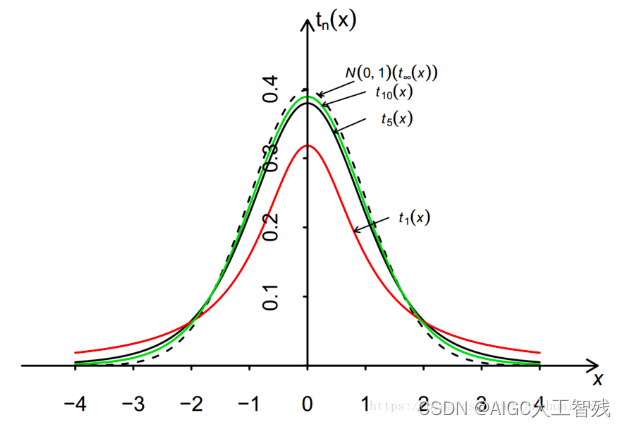
• t分布：又叫学生分布，是小样本分布，当t分布随着自由度v的增大越来越趋近于正态分布。
  

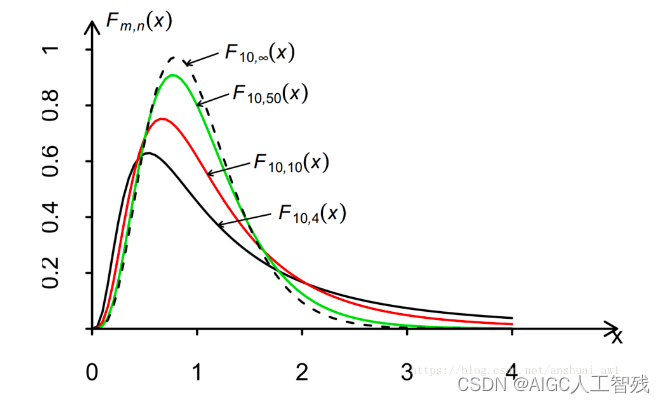
• F分布：两个独立变量组成的概率密度分布。
  

• 卡方分布：卡方分布通常用于假设检验，特别是拟合优度的卡方检验。