详细解说堆的结构

知道堆这种数据结构吗？

建堆的过程是什么样的？

堆是一颗完全二叉树。

在这棵树中，所有父节点都满足大于等于其子节点的堆叫大根堆。

所有父节点都满足小于等于其子节点的堆叫小根堆。

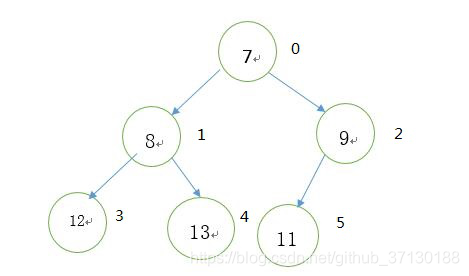
堆虽然是一颗树，但是通常存放在一个数组中，父节点和孩子节点的父子关系通过数组下标来确定。如下图的小根堆及存储它的数组： 

创建

除了知道怎么计算一个节点的父节点和孩子节点的索引外，我们还需要两个算法，即保持堆的性质和建堆。我们将看到建堆的方法对大根堆和小根堆也是一样的。

保持堆的性质：

保持堆的性质，对大根堆和小根堆很相似，但不完全一样，所以得分开说。

1. 对大根堆来说是：已经存在两个大根堆，现在要把一个元素作为这两个大根堆根的父节点，构成一个新的堆，但是这个堆的根结点可能不满足大根堆的性质，也就是说，它可能比它的孩子节点小，所以需要对它进行操作。

操作的方式就是，我们从这个节点和它的孩子节点中选出最大的，如果最大的节点是这个节点本身，堆就已经满足大根堆性质了。

否则，将这个节点与最大节点交换，交换后该节点在新的位置上也可能违背大根堆性质，所以需要递归的进行，直至这个节点比孩子节点都大或者是子节点为止（这个过程也叫做元素下降，因为元素从根结点开始一步一步往下移）（符合就成了；不符合就交换数值然后递归，直到符合成了）。

（2）对小根堆：保持堆的性质，过程是，已经存在两个小根堆，现在要把一个元素作为这两个堆的根，作为新的小根堆，但是这个元素可能会违背小根堆的性质，所以需要将它下降（也就是说，不断将它与它和孩子节点中的最小节点交换，直到它是它和它孩子节点中最小的或者是叶子节点为止）。对应的Java代码如下：

有了上面的这些准备工作，我们终于可以建堆了。正如前面所说，建堆的过程对大根堆和小根堆是一样的。我们可以把单个元素看作大根堆或者小根堆。假设数组中最后一个堆元素的下标为i，则数组中从0下标开始，最后一个有孩子节点的元素就是j=parent(i)。于是，我们从j到0，对一个元素都调用heapify方法，堆就建好了。下图是算法导论给出的伪代码：

可以用堆构建优先级队列，因为我们可以在常数时间内获得堆中（优先级）最大或者最小的元素，这对于优先级队列来说是很重要的。（可能就是排大根堆跟小根堆）