title:排序
date:2022-10-23 22:52:16
description:数组排序(快排,堆排,归并,冒泡),链表排序(归并)
categories:LeetCode 学习笔记
tags:排序
1.排序理论
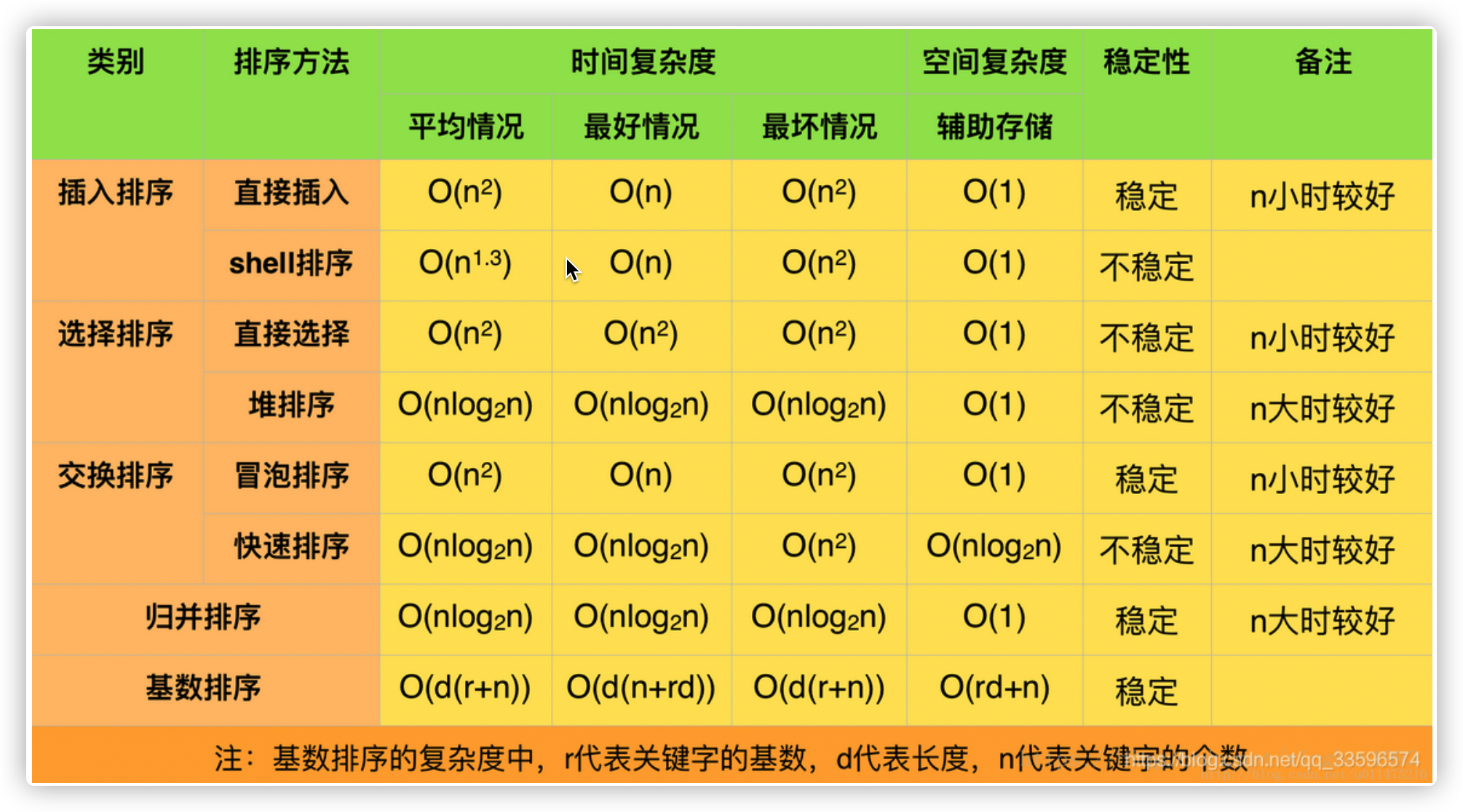
题目:215
快排是一种递归的算法,所以会形成一个树型结构,最优的情况下,树的两侧都比较平衡,最优的时间复杂度 O(NlongN)
但是最坏的情况下会生成一个单侧树,时间复杂度 O(N2)
1.2 自定义排序规则
有时候我们需要升序或者降序排序,又或者对第一维度升序对第二维度降序,那么下面的方法就是自定义排序规则
1.2.1 重写 sort 方法
sort 方法第三个参数接受一个排序规则,我们只需要将排序规则重新定义即可。这个可以具体借鉴 1.2.2 中自定义的排序函数
1.2.2 STL 容器所接受的排序对象
比如说像大小根堆中的元素就是有序的,所以我们可以定义其排序规则。默认情况下创建的是大根堆
// 1. 先创建自定义的排序类
class mycomparison{
public:
bool operator()(const pair<int,int>& lhs,const pair<int,int>& rhs){
return lhs.second>rhs.second; // 构建小根堆
}
};
// 2.创建小根堆
priority_queue<pair<int,int>,vector<pair<int,int>>,mycomparison> pri_que;
1.2.2 二维数组的排序
这里我们要重写 sort 方法,因为 sort 方法第三个传输传入的是排序准则。
假设说现在我们想让 [x1,x2] 中 x1 升序的情况下 x2 降序,那么就应该像下面一样写代码
下面的意思是说
如果第一维度是相同的:按照第二维度进行降序排序
**第一维度是不相同的:**按照第一维度升序排序
最后就将该方法名传入
static bool comp(vector<int>& a,vector<int>& b){
if(a[0]==b[0]) return a[1]>b[1]; //
return a[0]<b[0]; // 如果 x1 维度是不相同的
}
sort(envelopes.begin(),envelopes.end(),comp);
这个方法也可以协程匿名函数的形式。在这里使用隐式返回的方法。就需要写返回值类型
sort(envelopes.begin(),envelopes.end(),[](vector<int>& a,vector<int>& b){
if(a[0]==b[0]) return a[1]>b[1]; // 降序
return a[0]<b[0];
});
2.八大排序算法
2.1_快速排序
2.1.1 算法描述
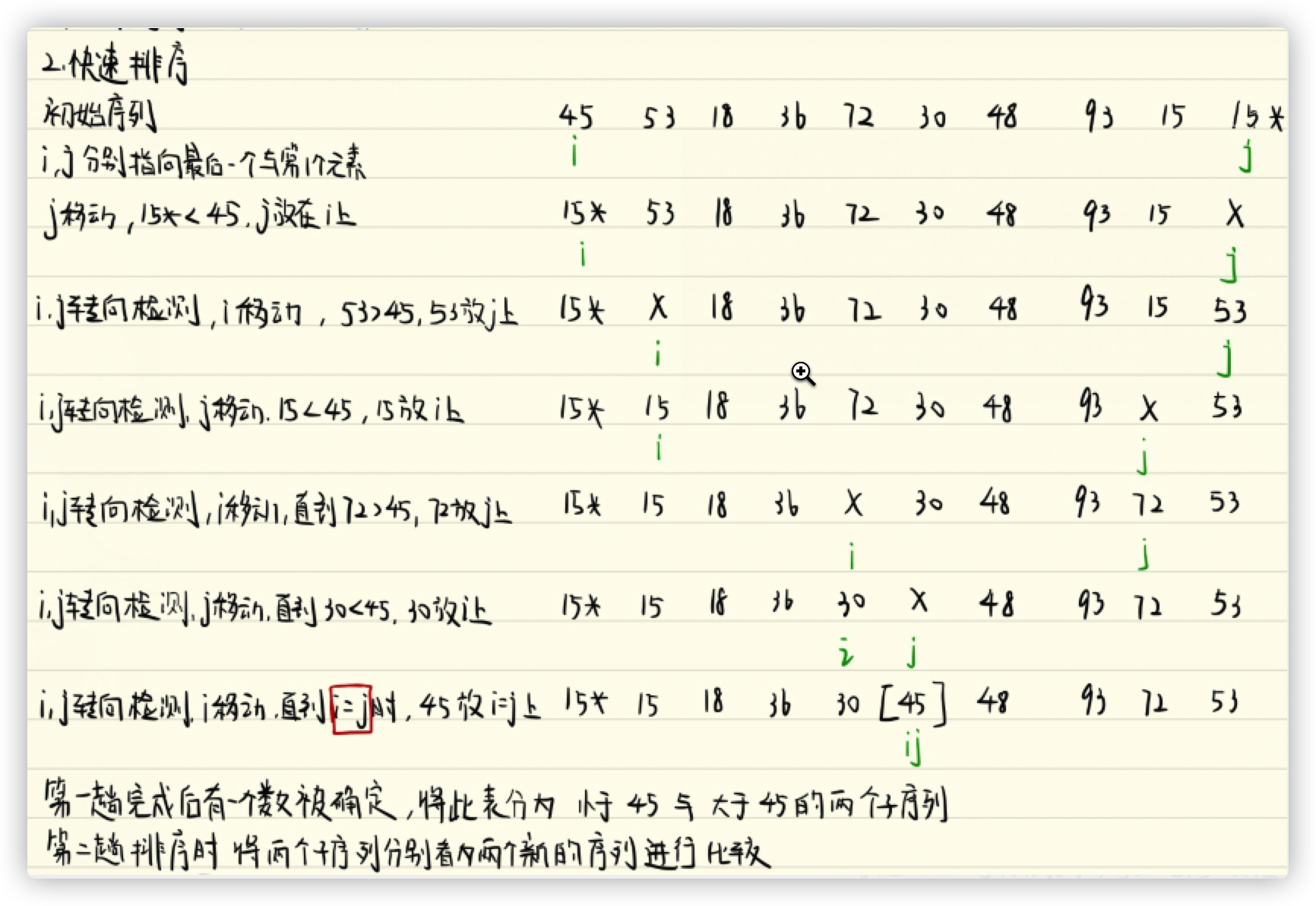
参考算法
关键:有两个指针 i,j 。有一个 temp ,先判断 j 再判断 i ,当“满足”时,i 或 j 就移动,不满足时 i,j 交换位置
2.1.2 代码实现
class Solution {
public:
void quick_sort(vector<int>&nums,int left,int right){
if(left<right){ // 结束递归的条件
int i = left;
int j = right;
int temp = nums[left];
// 开始快速遍历
while(i<j){
// 先判断 j
while(i<j&&nums[j]>=temp) j--; // 如果 j 指向元素一直>= temp 就不交换
if(i<j){ // 不满足上述条件了
nums[i] = nums[j]; // 将 j 放在 i 上,j 的位置变为 x
i++; // i 的 x 被占了,开始进行 i 的判断
}
// 然后判断 i
while(i<j&&nums[i]<temp) i++;
if(i<j){
nums[j] = nums[i]; // 将 j 放在 i 的 x 上
j--; // j 的坑被占,继续 j 的判断
}
}
nums[i] = temp; // i,j 都遍历完成后将 temp 放在 i 的位置,因为最后 i 上是挖坑了的
// 将 temp 为分界点然后对剩余的左右量变数组进行遍历操作
quick_sort(nums,left,i-1); // nums 左边
quick_sort(nums,i+1,right); // nums 右边
}
}
int findKthLargest(vector<int>& nums, int k) {
// 对 nums 进行排序
quick_sort(nums,0,nums.size()-1);
// 取前 k 个值
return nums[nums.size()-k];
}
};
2.3 912堆排序
2.3.1 算法描述
使用大根堆排序的算法有两步:
①节点调整:向下调整,即不断将 cur 和其左右子树进行交换。最后生成的结果是父节点的值一定会大于左右两个节点
②最大堆:对于每一个父节点都要走节点调整的步骤
③每次迭代得到堆的最大值:上面的步骤只能确保堆顶是最大值,不确定父结点两个孩子谁大。所以每一次生成大根堆后需要交换节点重新得到第二大的数
排序部分算法:
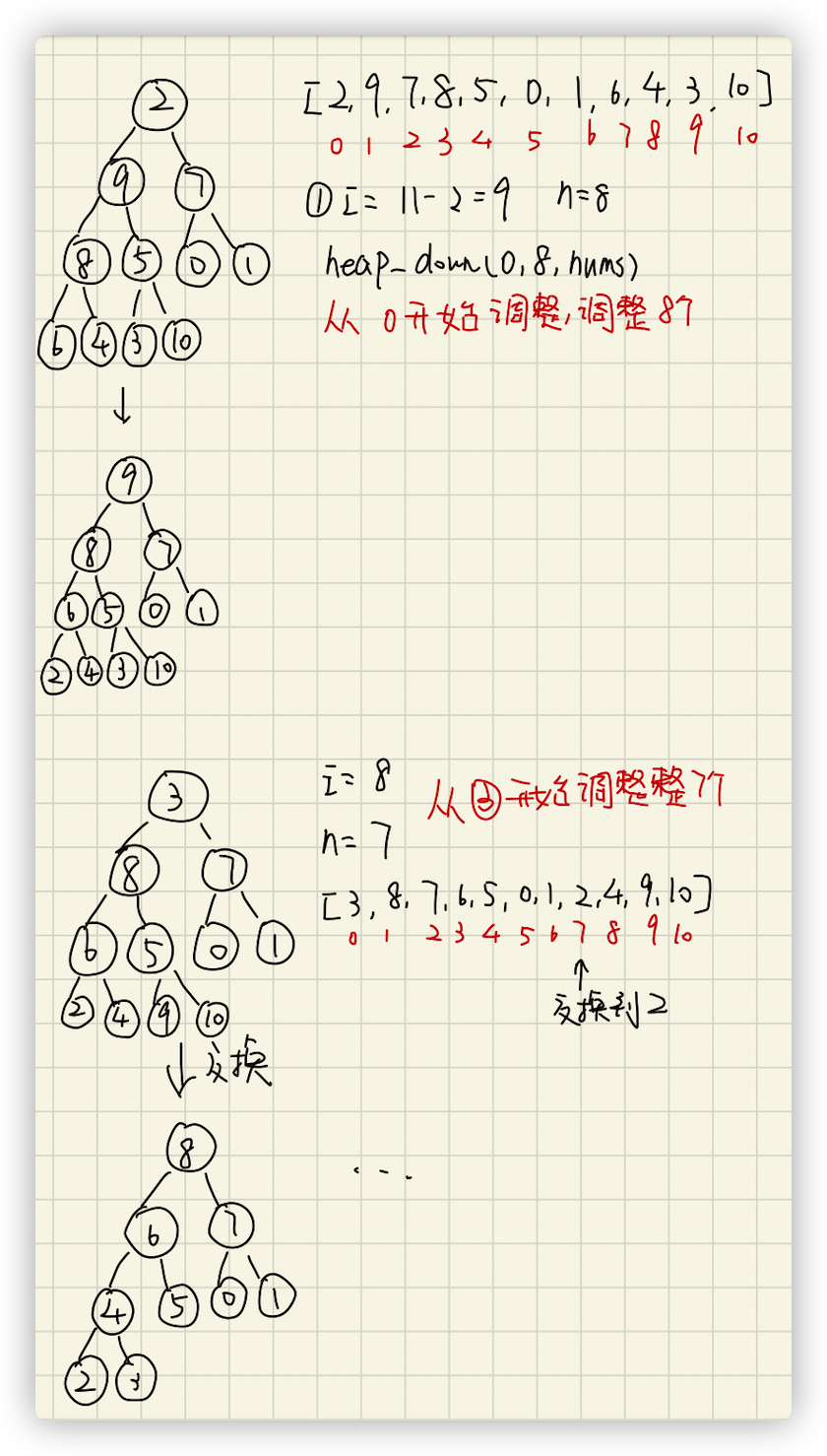
从代码角度来说需要如下定义;
(1) head_down
该函数调整 nums[cur] 节点在最大堆中的位置
(2)maxHeapity
函数是构建整个堆为大根堆。 调整的起始位置在 n/2-1 开始,因为在 n/2 后面的节点都是叶子节点,交换是从父结点开始交换的。
(3)sortArray
每次我们会从大根堆中拿到最大的节点放在堆最后的位置,然后再重新生成大根堆
class Solution {
public:
void head_down(vector<int>& nums,int cur,int n){
while(cur<n){
int left = 2*cur+1;
int right = 2*cur+2;
int max_val = nums[cur];
int max_inx = cur;
if(left<n && max_val<nums[left]){
max_val = nums[left];
max_inx = left;
}
if(right<n&&max_val<nums[right]){
max_val = nums[right];
max_inx = right;
}
if(max_inx==cur) break;
swap(nums[cur],nums[max_inx]);
cur = max_inx;
}
}
void maxHeap(vector<int>& nums){
int n = nums.size();
for(int i = n/2-1;i>=0;i--){
head_down(nums,i,n);
}
}
vector<int> sortArray(vector<int>& nums) {
// 创建堆,得到最大堆
int n = nums.size();
maxHeap(nums);
for(int i = n-1;i>0;i--){
swap(nums[0],nums[i]);
head_down(nums,0,i);
}
return nums;
}
};
2.4 归并排序
2.4.1 算法描述
归并排序是递归的方式,该算法采用经典的分治。分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起
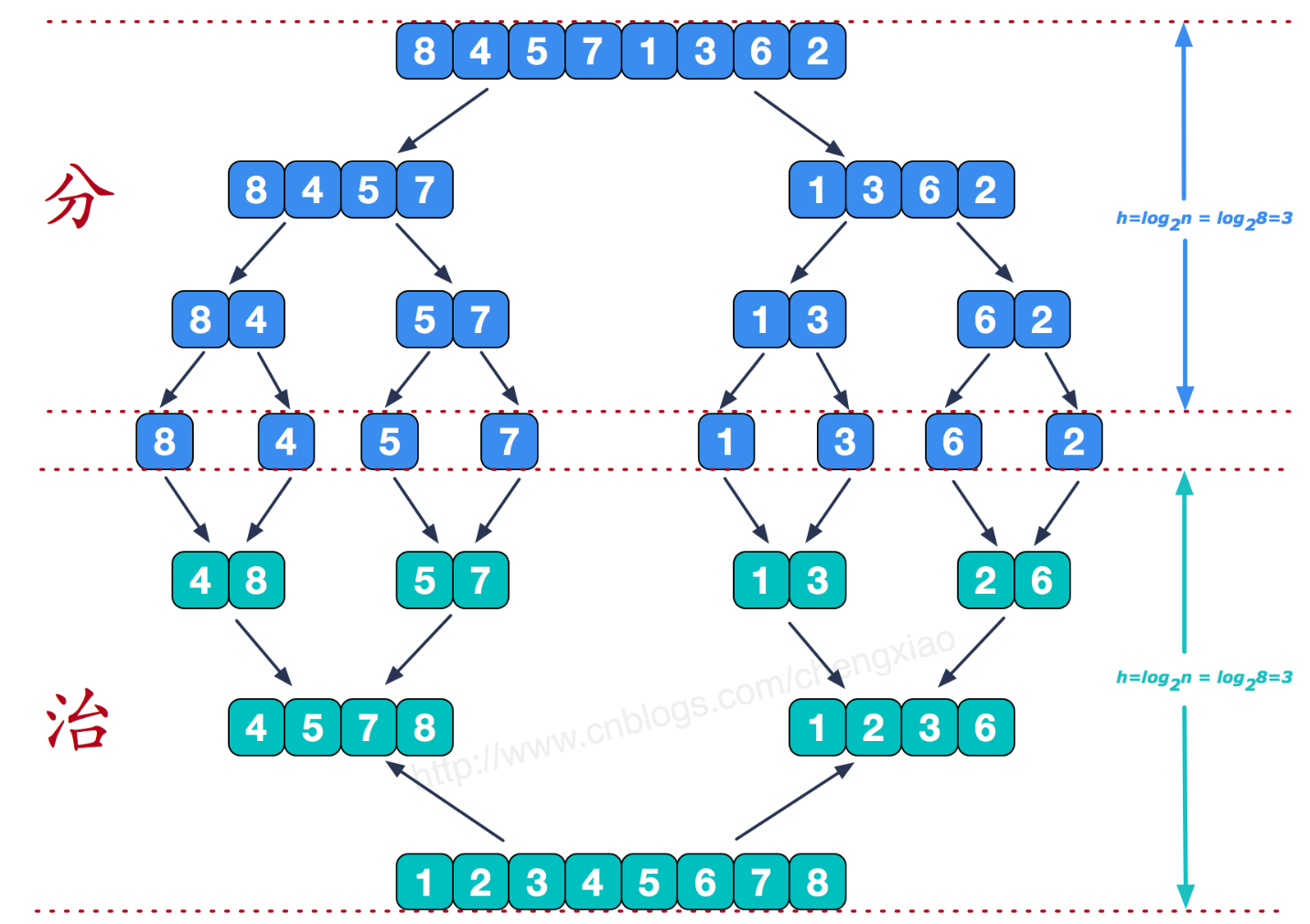
这里在区分做区间和右区间时还是遵循 [left,mid],[mid+1,right] 的原则
如上图所示将左右两边的数组一直向下分,直到分到 left==right ,就返回。那么第一个进行 merge 的数组 left = 0,right = 1

这里 ans 的目的就是存放区间 [left,mid]&[mid+1,right]多出来的那些值
如果是有多个数组 [5,4,3,2,1,0] 那么排序的 index 就为
0,1;0,2;3,4;4,5;0,5
2.4.2 代码实现
class Solution {
public:
// merge 的方法
void merge(vector<int>& nums,int left,int right,vector<int>& ans){
int mid = left+(right-left)/2;
int i = left; // 左边数组的头区间
int j = mid+1; // 右边区间的头区间
int k = 0; // ans 的起始
while(i<=mid&&j<=right){ // 两个区间内的元素不断比较
if(nums[i]<=nums[j]) ans[k++] = nums[i++];
else ans[k++] = nums[j++];
}
// 放置剩余元素
while(i<=mid) ans[k++] = nums[i++];
while(j<=right) ans[k++] = nums[j++];
// 将 ans 赋值给 nums
for(int i = left;i<=right;i++){
nums[i] = ans[i-left];
}
}
void mergeSort(vector<int>& nums,int left,int right,vector<int>& ans){
if(left>=right) return;
int mid = left+(right-left)/2;
mergeSort(nums,left,mid,ans);
mergeSort(nums,mid+1,right,ans);
// 合并
merge(nums,left,right,ans);
}
vector<int> sortArray(vector<int>& nums) {
vector<int> ans(nums.size());
mergeSort(nums,0,nums.size()-1,ans);
return nums;
}
};
2.6 冒泡排序
交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
i 控制有几个值已经冒完了,如果数组的大小为 n ,那么需要冒 n 次
j 控制这一次要交换多少次,如果 i = 1 ,那就代表有一个值冒了出来,后面排序需要交换 n-i-1 次
在每一次冒的时候将冒好的值放在最后。如果在每次冒的时候该值没有任何的交换则说明数组已经有序
2.6.1 算法描述
注意 for 循环当中 i,j 的初始值
class Solution {
public:
vector<int> sortArray(vector<int>& nums) {
int n = nums.size();
for(int i = 0;i<n;i++){
bool isexchange = false;
for(int j = 0;j<n-i-1;j++){
if(nums[j+1]<nums[j]){
swap(nums[j],nums[j+1]);
isexchange = true;
}
}
if(isexchange==false) return nums;
}
return nums;
}
};
2.7_148 排序链表
2.7.1 算法描述
这里是用归并的方法对两个链表进行排序,思路比较常见。
对比链表来说比较难的就是找到其中间节点然后将这个链表一份为二。
归并思路:
①找到其 left ,mid ,right 节点,并且用递归的方式寻找,直到找到单独的两个节点
②将排好序的 list 进行合并,就是两个有序链表合并的方法
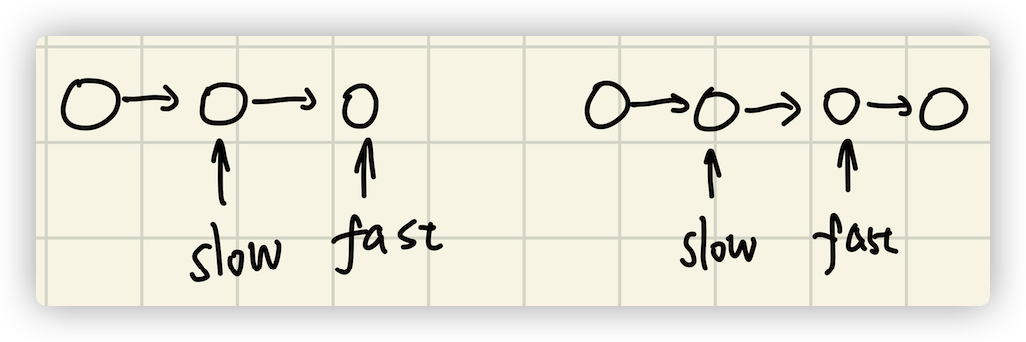
如何找到中间节点:
使用快慢指针,不管是链表中的 node 是奇数还是偶数都可,都能让 slow 指向之间节点
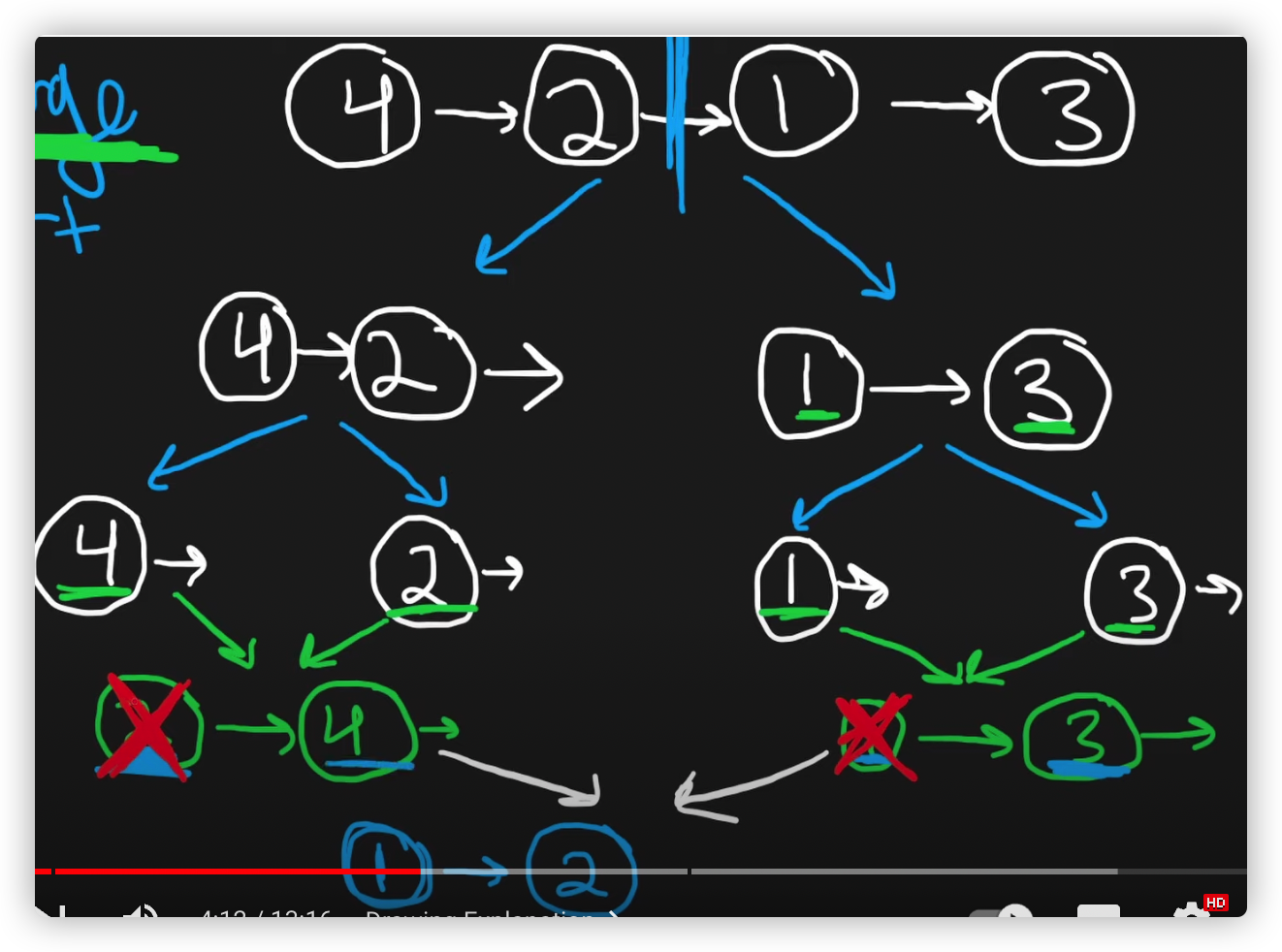
归并排序的排序顺序:

2.7.2 代码实现
class Solution {
public:
// 两个链表的排序
ListNode* merge(ListNode* list1,ListNode* list2){
ListNode* dummy = new ListNode();
ListNode* pre = dummy;
while(list1!=nullptr&&list2!=nullptr){
// 判断大小
if(list1->val<list2->val){
pre->next = list1;
list1 = list1->next;
}else{
pre->next = list2;
list2 = list2->next;
}
pre = pre->next;
}
// 肯定有一个为 null
if(list1==nullptr) pre->next = list2;
else pre->next = list1;
return dummy->next;
}
// 使用快慢指针得到中间节点
ListNode* getMid(ListNode* head){
ListNode* fast = head;
ListNode* slow = head;
while(fast->next!=nullptr&&fast->next->next!=nullptr){
fast = fast->next->next;
slow = slow->next;
}
return slow;
}
ListNode* split(ListNode* left,ListNode* right){
if(left==right) return left;
// 找到中间节点
ListNode* mid = getMid(left);
ListNode* mid_next = mid->next;
mid->next = nullptr;
ListNode* left_res = split(left,mid);
ListNode* right_res = split(mid_next,right);
ListNode* res = merge(left_res,right_res);
return res;
}
ListNode* sortList(ListNode* head) {
return split(head,nullptr);
}
};
2.7.3 时空复杂度
时间复杂度:O(NlogN)
空间复杂度:O(N) 最坏情况
2.8_剑指 Offer 51. 数组中的逆序对
2.8.1 算法描述
这里使用归并排序的方法,将数组分成两个 part ,在最后 merge 的时候,左边的 part 内部是有序的,右边的 part 内部也是有序的。
那么就要看 part2 中元素在 part1 中有几个是无序的,需要有两个指针将左右 part 放到数组中

所以在 merge 方法中当向 ans 中放置 nums[j] 时我们要先判断 nums[j] 之前有几个还有几个 i 是没有放到 ans 中的,这些值都比 nums[j] 要大,所以这些值中存在逆序对
易错点:
当 nums[i] == nums[j] 时我们应该放的是 nums[i] ,而不是 nums[j] ,所以在这两个值相等时不需要 对 count ++
2.8.2 代码实现
class Solution {
public:
/* 合并有序数组 */
int merge(vector<int>& nums, int left, int mid, int right) {
int idx = 0;
int i = left;
int j = mid + 1;
int ans = 0;
while (i <= mid && j <= right) {
if (nums[i] > nums[j]) {
ans += mid - i + 1; /* 统计逆序对 */
tmp[idx++] = nums[j++];
} else {
tmp[idx++] = nums[i++];
}
}
/* 处理剩余数组 */
while (i <= mid) {
tmp[idx++] = nums[i++];
}
while (j <= right) {
tmp[idx++] = nums[j++];
}
/* 写到原数组中 */
for (int k = 0; k < idx; k++) {
nums[left + k] = tmp[k];
}
return ans;
}
/* 归并排序 */
int mergeSort(vector<int>& nums, int l, int r) {
if (l >= r) {
return 0;
}
int m = l + (r - l) / 2;
int revCnt = mergeSort(nums, l, m) + mergeSort(nums, m + 1, r);
return revCnt + merge(nums, l, m ,r);
}
int reversePairs(vector<int>& nums) {
int n = nums.size();
tmp = vector<int>(n);
return mergeSort(nums, 0, n - 1);
}
vector<int> tmp;
};
2.8.3 时空复杂度
时间复杂度:O(nlogn)
空间复杂度:O(n)
2.5_179最大数
2.5.1 算法描述
这里使用自定义的比较规则。两两 string 类型的值先进性拼接,然后再判断大小
这里有两点需要注意:
①如何定义拼接规则
②如何调用比较的函数
①如何定义比较规则
-
comparison 函数一定是 static 类型的。因为 sort 是全局函数,全局函数不能调用非静态成员变量
-
参数传入两个值,一个代表前一个,一个代表后一个
-
left < right --> 升序;left>right --> 降序
-
最后返回的是 bool 类型的数,将判断结果传入
②如何调用比较函数
- 如果是 STL 需要定义一个类,在类中重写operator 方法,然后在泛型中传入 comparison 类名
- 如果是 sort 需要将函数名定义出来就像这个题一样
易错点:
如果 res[0] == “0” 则说明 0 是最大值,后面的值全是 0 ,那么直接返回 0 就好
2.5.2 代码实现
class Solution {
public:
static bool comparison(string left,string right){
return left+right>right+left; // 字符串拼接
}
string largestNumber(vector<int>& nums) {
// 1. 将 nums 转换成 string
vector<string> str_vec;
for(int i : nums){
str_vec.push_back(to_string(i));
}
// 2. 对 str_vec 按照降序排序,但是不是直接降序需要将两个数进行累加
sort(str_vec.begin(),str_vec.end(),comparison);
// 3. 拼接结果
if(str_vec[0]=="0") return "0";
string res = "";
for(string s: str_vec){
res+=s;
}
return res;
}
};
2.5.3 时空复杂度
时间复杂度:O(nlognlogm)
空间复杂度:O()





















 3145
3145

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








